Data-driven 2D stationary quantum droplets and wave propagations in the amended GP equation with two potentials via deep neural networks learning

In this paper, we develop a systematic deep learning approach to solve two-dimensional (2D) stationary quantum droplets (QDs) and investigate their wave propagation in the 2D amended Gross-Pitaevskii equation with Lee-Huang-Yang correction and two kinds of potentials. Firstly, we use the initial-value iterative neural network (IINN) algorithm for 2D stationary quantum droplets of stationary equations. Then the learned stationary QDs are used as the initial value conditions for physics-informed neural networks (PINNs) to explore their evolutions in the some space-time region. Especially, we consider two types of potentials, one is the 2D quadruple-well Gaussian potential and the other is the PT-symmetric HO-Gaussian potential, which lead to spontaneous symmetry breaking and the generation of multi-component QDs. The used deep learning method can also be applied to study wave propagations of other nonlinear physical models.

Two-stage initial-value iterative physics-informed neural networks for simulating solitary waves of nonlinear wave equations

We propose a new two-stage initial-value iterative neural network (IINN) algorithm for solitary wave computations of nonlinear wave equations based on traditional numerical iterative methods and physics-informed neural networks (PINNs). Specifically, the IINN framework consists of two subnetworks, one of which is used to fit a given initial value, and the other incorporates physical information and continues training on the basis of the first subnetwork. Importantly, the IINN method does not require any additional data information including boundary conditions, apart from the given initial value. Corresponding theoretical guarantees are provided to demonstrate the effectiveness of our IINN method. The proposed IINN method is efficiently applied to learn some types of solutions in different nonlinear wave equations, including the one-dimensional (1D) nonlinear Schr\"odinger equations (NLS) equation (with and without potentials), the 1D saturable NLS equation with PT -symmetric optical lattices, the 1D focusing-defocusing coupled NLS equations, the KdV equation, the two-dimensional (2D) NLS equation with potentials, the 2D amended GP equation with a potential, the (2+1)-dimensional KP equation, and the 3D NLS equation with a potential. These applications serve as evidence for the efficacy of our method. Finally, by comparing with the traditional methods, we demonstrate the advantages of the proposed IINN method.

Deep learning soliton dynamics and complex potentials recognition for 1D and 2D PT-symmetric saturable nonlinear Schrödinger equations

In this paper, we firstly extend the physics-informed neural networks (PINNs) to learn data-driven stationary and non-stationary solitons of 1D and 2D saturable nonlinear Schr\"odinger equations (SNLSEs) with two fundamental PT-symmetric Scarf-II and periodic potentials in optical fibers. Secondly, the data-driven inverse problems are studied for PT-symmetric potential functions discovery rather than just potential parameters in the 1D and 2D SNLSEs. Particularly, we propose a modified PINNs (mPINNs) scheme to identify directly the PT potential functions of the 1D and 2D SNLSEs by the solution data. And the inverse problems about 1D and 2D PT -symmetric potentials depending on propagation distance z are also investigated using mPINNs method. We also identify the potential functions by the PINNs applied to the stationary equation of the SNLSE. Furthermore, two network structures are compared under different parameter conditions such that the predicted PT potentials can achieve the similar high accuracy. These results illustrate that the established deep neural networks can be successfully used in 1D and 2D SNLSEs with high accuracies. Moreover, some main factors affecting neural networks performance are discussed in 1D and 2D PT Scarf-II and periodic potentials, including activation functions, structures of the networks, and sizes of the training data. In particular, twelve different nonlinear activation functions are in detail analyzed containing the periodic and non-periodic functions such that it is concluded that selecting activation functions according to the form of solution and equation usually can achieve better effect.

Data-driven localized waves and parameter discovery in the massive Thirring model via extended physics-informed neural networks with interface zones

In this paper, we study data-driven localized wave solutions and parameter discovery in the massive Thirring (MT) model via the deep learning in the framework of physics-informed neural networks (PINNs) algorithm. Abundant data-driven solutions including soliton of bright/dark type, breather and rogue wave are simulated accurately and analyzed contrastively with relative and absolute errors. For higher-order localized wave solutions, we employ the extended PINNs (XPINNs) with domain decomposition to capture the complete pictures of dynamic behaviors such as soliton collisions, breather oscillations and rogue-wave superposition. In particular, we modify the interface line in domain decomposition of XPINNs into a small interface zone and introduce the pseudo initial, residual and gradient conditions as interface conditions linked adjacently with individual neural networks. Then this modified approach is applied successfully to various solutions ranging from bright-bright soliton, dark-dark soliton, dark-antidark soliton, general breather, Kuznetsov-Ma breather and second-order rogue wave. Experimental results show that this improved version of XPINNs reduce the complexity of computation with faster convergence rate and keep the quality of learned solutions with smoother stitching performance as well. For the inverse problems, the unknown coefficient parameters of linear and nonlinear terms in the MT model are identified accurately with and without noise by using the classical PINNs algorithm.

Deep neural networks for solving forward and inverse problems of -dimensional nonlinear wave equations with rational solitons

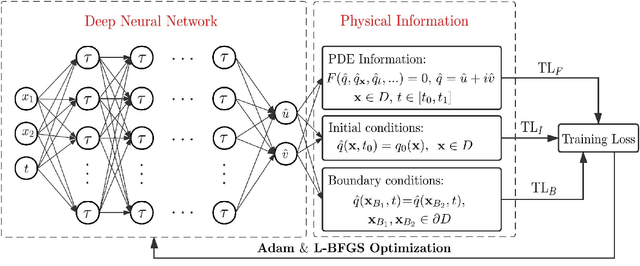
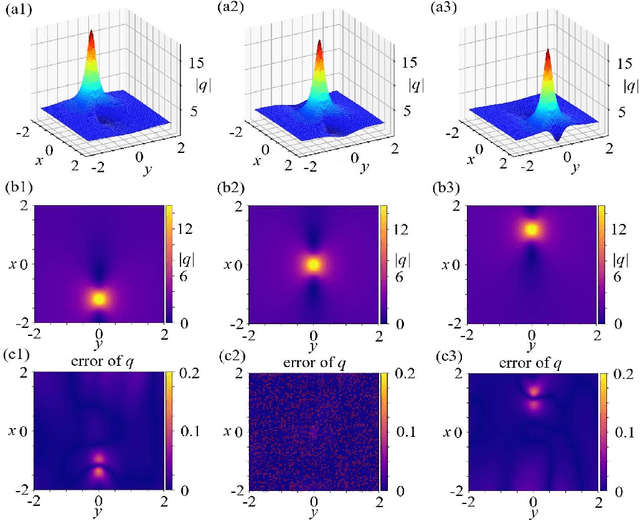
In this paper, we investigate the forward problems on the data-driven rational solitons for the (2+1)-dimensional KP-I equation and spin-nonlinear Schr\"odinger (spin-NLS) equation via the deep neural networks leaning. Moreover, the inverse problems of the (2+1)-dimensional KP-I equation and spin-NLS equation are studied via deep learning. The main idea of the data-driven forward and inverse problems is to use the deep neural networks with the activation function to approximate the solutions of the considered (2+1)-dimensional nonlinear wave equations by optimizing the chosen loss functions related to the considered nonlinear wave equations.

Data-driven discovery of Bäcklund transforms and soliton evolution equations via deep neural network learning schemes

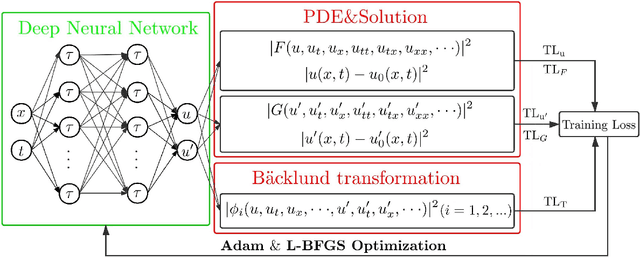
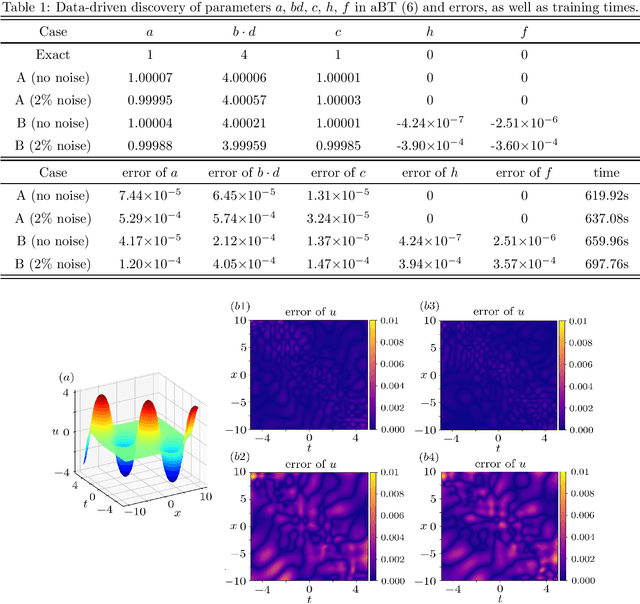
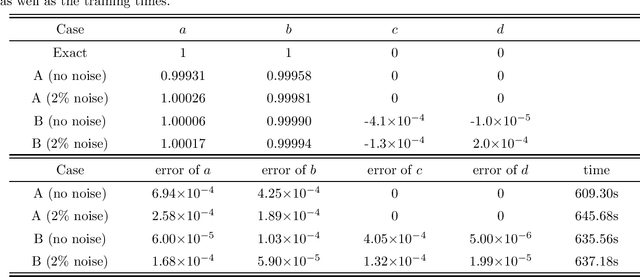
We introduce a deep neural network learning scheme to learn the B\"acklund transforms (BTs) of soliton evolution equations and an enhanced deep learning scheme for data-driven soliton equation discovery based on the known BTs, respectively. The first scheme takes advantage of some solution (or soliton equation) information to study the data-driven BT of sine-Gordon equation, and complex and real Miura transforms between the defocusing (focusing) mKdV equation and KdV equation, as well as the data-driven mKdV equation discovery via the Miura transforms. The second deep learning scheme uses the explicit/implicit BTs generating the higher-order solitons to train the data-driven discovery of mKdV and sine-Gordon equations, in which the high-order solution informations are more powerful for the enhanced leaning soliton equations with higher accurates.

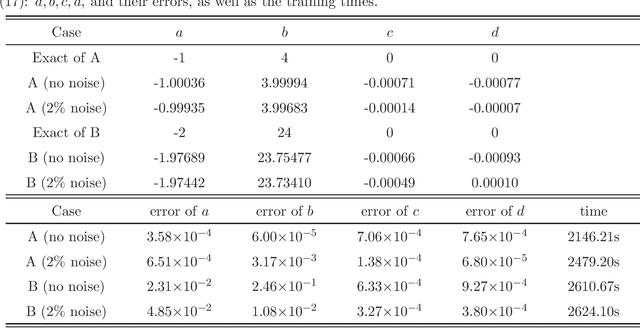
Deep learning neural networks for the third-order nonlinear Schrodinger equation: Solitons, breathers, and rogue waves

The third-order nonlinear Schrodinger equation (alias the Hirota equation) is investigated via deep leaning neural networks, which describes the strongly dispersive ion-acoustic wave in plasma and the wave propagation of ultrashort light pulses in optical fibers, as well as broader-banded waves on deep water. In this paper, we use the physics-informed neural networks (PINNs) deep learning method to explore the data-driven solutions (e.g., soliton, breather, and rogue waves) of the Hirota equation when the two types of the unperturbated and unperturbated (a 2% noise) training data are considered. Moreover, we use the PINNs deep learning to study the data-driven discovery of parameters appearing in the Hirota equation with the aid of solitons.

Data-driven peakon and periodic peakon travelling wave solutions of some nonlinear dispersive equations via deep learning

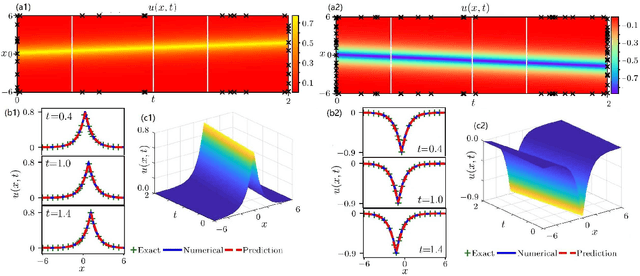
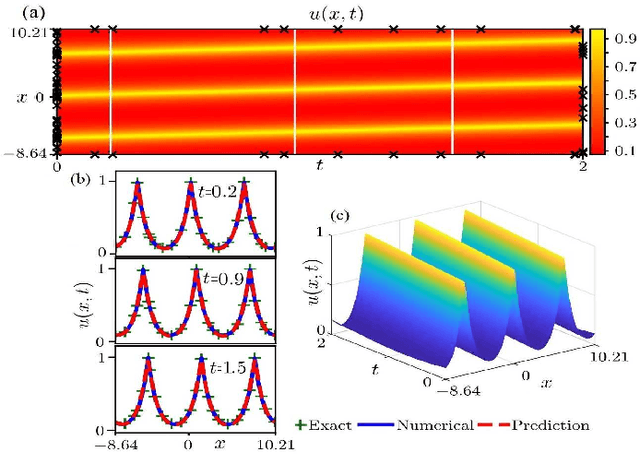
In the field of mathematical physics, there exist many physically interesting nonlinear dispersive equations with peakon solutions, which are solitary waves with discontinuous first-order derivative at the wave peak. In this paper, we apply the multi-layer physics-informed neural networks (PINNs) deep learning to successfully study the data-driven peakon and periodic peakon solutions of some well-known nonlinear dispersion equations with initial-boundary value conditions such as the Camassa-Holm (CH) equation, Degasperis-Procesi equation, modified CH equation with cubic nonlinearity, Novikov equation with cubic nonlinearity, mCH-Novikov equation, b-family equation with quartic nonlinearity, generalized modified CH equation with quintic nonlinearity, and etc. These results will be useful to further study the peakon solutions and corresponding experimental design of nonlinear dispersive equations.

Data-driven rogue waves and parameter discovery in the defocusing NLS equation with a potential using the PINN deep learning

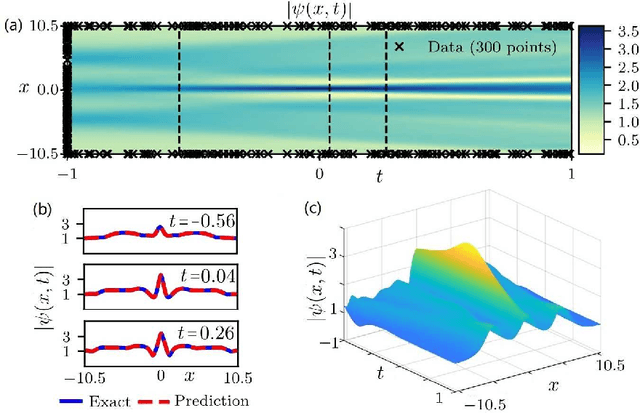
The physics-informed neural networks (PINNs) can be used to deep learn the nonlinear partial differential equations and other types of physical models. In this paper, we use the multi-layer PINN deep learning method to study the data-driven rogue wave solutions of the defocusing nonlinear Schr\"odinger (NLS) equation with the time-dependent potential by considering several initial conditions such as the rogue wave, Jacobi elliptic cosine function, two-Gaussian function, or three-hyperbolic-secant function, and periodic boundary conditions. Moreover, the multi-layer PINN algorithm can also be used to learn the parameter in the defocusing NLS equation with the time-dependent potential under the sense of the rogue wave solution. These results will be useful to further discuss the rogue wave solutions of the defocusing NLS equation with a potential in the study of deep learning neural networks.