Delay-Adaptive Learning in Generalized Linear Contextual Bandits

In this paper, we consider online learning in generalized linear contextual bandits where rewards are not immediately observed. Instead, rewards are available to the decision-maker only after some delay, which is unknown and stochastic. We study the performance of two well-known algorithms adapted to this delayed setting: one based on upper confidence bounds, and the other based on Thompson sampling. We describe modifications on how these two algorithms should be adapted to handle delays and give regret characterizations for both algorithms. Our results contribute to the broad landscape of contextual bandits literature by establishing that both algorithms can be made to be robust to delays, thereby helping clarify and reaffirm the empirical success of these two algorithms, which are widely deployed in modern recommendation engines.

Provably Efficient Reinforcement Learning with Aggregated States

We establish that an optimistic variant of Q-learning applied to a finite-horizon episodic Markov decision process with an aggregated state representation incurs regret $\tilde{\mathcal{O}}(\sqrt{H^5 M K} + \epsilon HK)$, where $H$ is the horizon, $M$ is the number of aggregate states, $K$ is the number of episodes, and $\epsilon$ is the largest difference between any pair of optimal state-action values associated with a common aggregate state. Notably, this regret bound does not depend on the number of states or actions. To the best of our knowledge, this is the first such result pertaining to a reinforcement learning algorithm applied with nontrivial value function approximation without any restrictions on the Markov decision process.

Balanced Linear Contextual Bandits

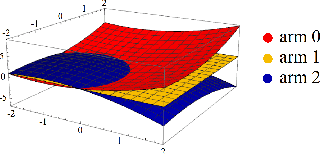
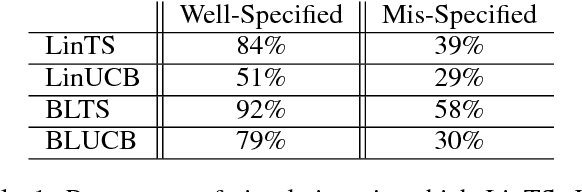
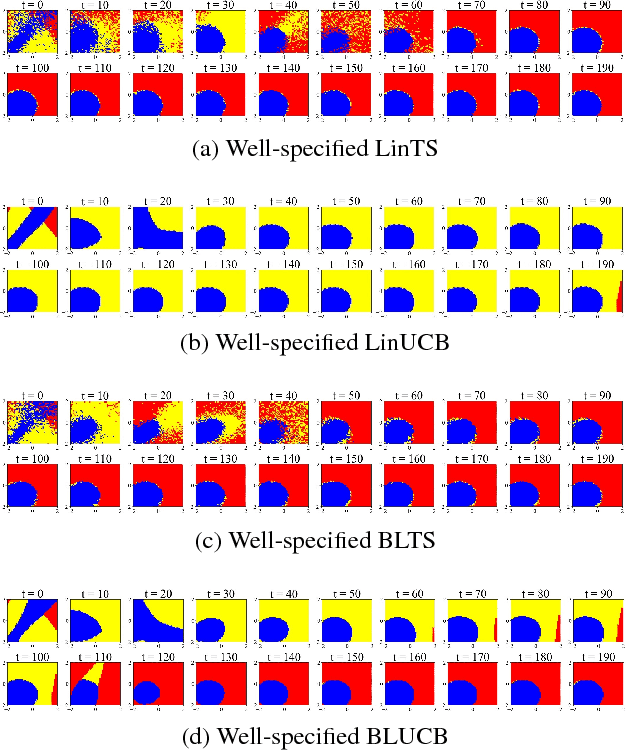
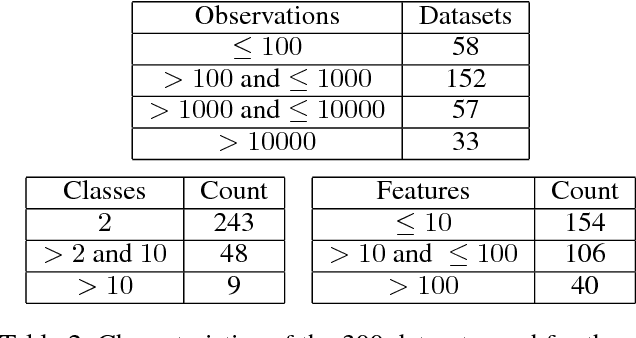
Contextual bandit algorithms are sensitive to the estimation method of the outcome model as well as the exploration method used, particularly in the presence of rich heterogeneity or complex outcome models, which can lead to difficult estimation problems along the path of learning. We develop algorithms for contextual bandits with linear payoffs that integrate balancing methods from the causal inference literature in their estimation to make it less prone to problems of estimation bias. We provide the first regret bound analyses for linear contextual bandits with balancing and show that our algorithms match the state of the art theoretical guarantees. We demonstrate the strong practical advantage of balanced contextual bandits on a large number of supervised learning datasets and on a synthetic example that simulates model misspecification and prejudice in the initial training data.

Offline Multi-Action Policy Learning: Generalization and Optimization

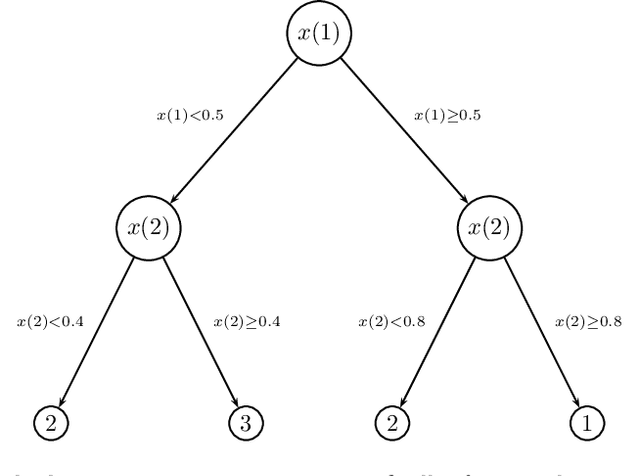
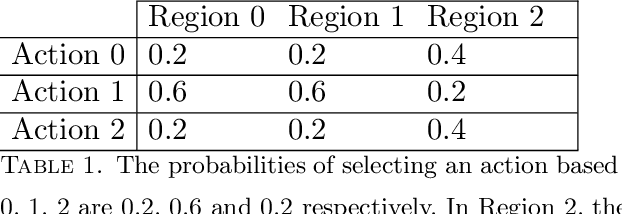
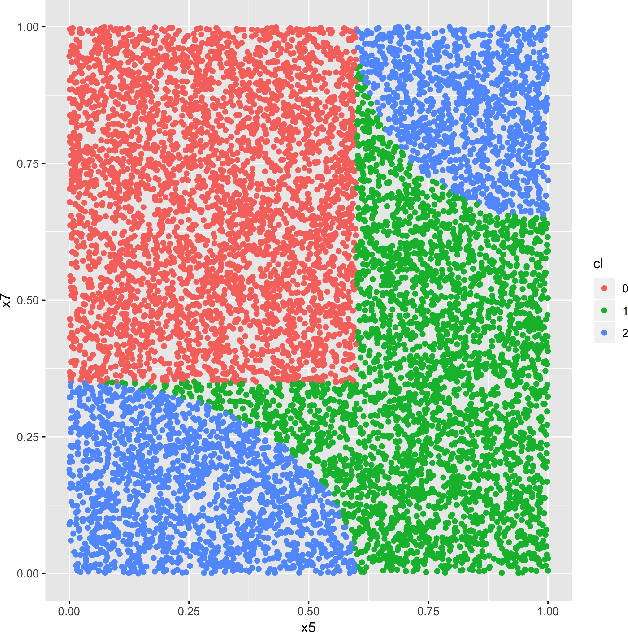
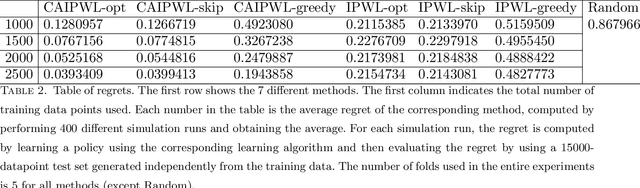
In many settings, a decision-maker wishes to learn a rule, or policy, that maps from observable characteristics of an individual to an action. Examples include selecting offers, prices, advertisements, or emails to send to consumers, as well as the problem of determining which medication to prescribe to a patient. While there is a growing body of literature devoted to this problem, most existing results are focused on the case where data comes from a randomized experiment, and further, there are only two possible actions, such as giving a drug to a patient or not. In this paper, we study the offline multi-action policy learning problem with observational data and where the policy may need to respect budget constraints or belong to a restricted policy class such as decision trees. We build on the theory of efficient semi-parametric inference in order to propose and implement a policy learning algorithm that achieves asymptotically minimax-optimal regret. To the best of our knowledge, this is the first result of this type in the multi-action setup, and it provides a substantial performance improvement over the existing learning algorithms. We then consider additional computational challenges that arise in implementing our method for the case where the policy is restricted to take the form of a decision tree. We propose two different approaches, one using a mixed integer program formulation and the other using a tree-search based algorithm.

MentorNet: Learning Data-Driven Curriculum for Very Deep Neural Networks on Corrupted Labels

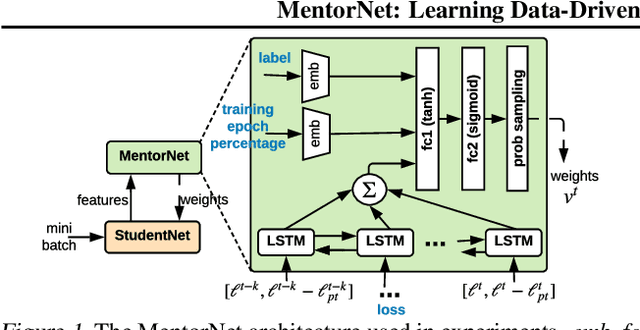
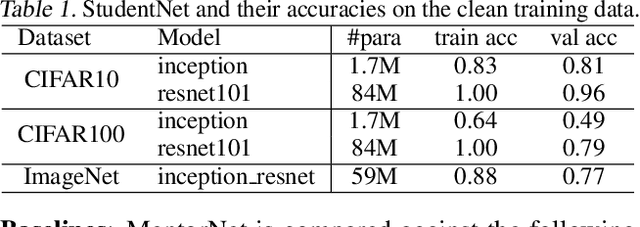
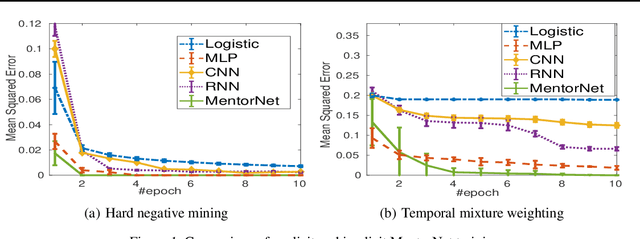
Recent deep networks are capable of memorizing the entire data even when the labels are completely random. To overcome the overfitting on corrupted labels, we propose a novel technique of learning another neural network, called MentorNet, to supervise the training of the base deep networks, namely, StudentNet. During training, MentorNet provides a curriculum (sample weighting scheme) for StudentNet to focus on the sample the label of which is probably correct. Unlike the existing curriculum that is usually predefined by human experts, MentorNet learns a data-driven curriculum dynamically with StudentNet. Experimental results demonstrate that our approach can significantly improve the generalization performance of deep networks trained on corrupted training data. Notably, to the best of our knowledge, we achieve the best-published result on WebVision, a large benchmark containing 2.2 million images of real-world noisy labels. The code are at https://github.com/google/mentornet

On the convergence of mirror descent beyond stochastic convex programming

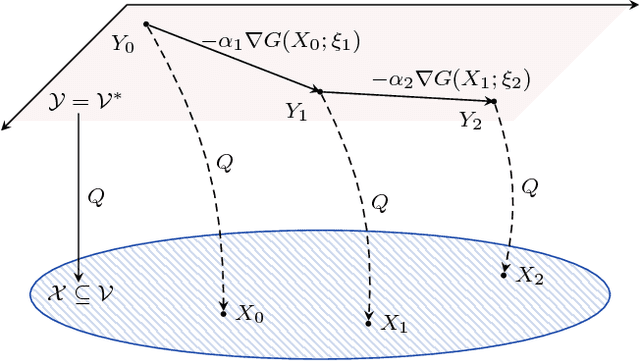
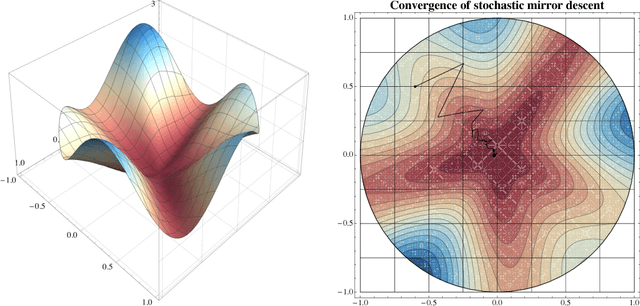
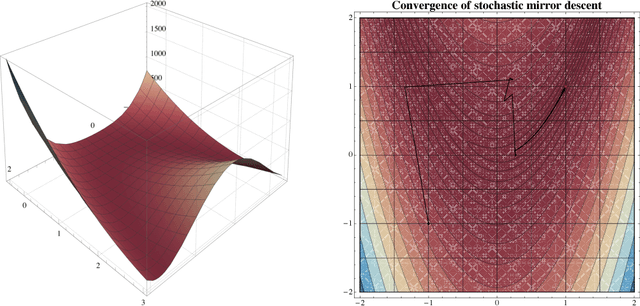
In this paper, we examine the convergence of mirror descent in a class of stochastic optimization problems that are not necessarily convex (or even quasi-convex), and which we call variationally coherent. Since the standard technique of "ergodic averaging" offers no tangible benefits beyond convex programming, we focus directly on the algorithm's last generated sample (its "last iterate"), and we show that it converges with probabiility $1$ if the underlying problem is coherent. We further consider a localized version of variational coherence which ensures local convergence of stochastic mirror descent (SMD) with high probability. These results contribute to the landscape of non-convex stochastic optimization by showing that (quasi-)convexity is not essential for convergence to a global minimum: rather, variational coherence, a much weaker requirement, suffices. Finally, building on the above, we reveal an interesting insight regarding the convergence speed of SMD: in problems with sharp minima (such as generic linear programs or concave minimization problems), SMD reaches a minimum point in a finite number of steps (a.s.), even in the presence of persistent gradient noise. This result is to be contrasted with existing black-box convergence rate estimates that are only asymptotic.

Learning in games with continuous action sets and unknown payoff functions

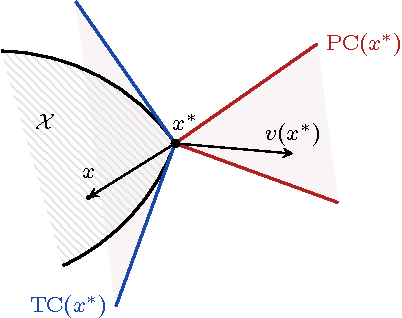
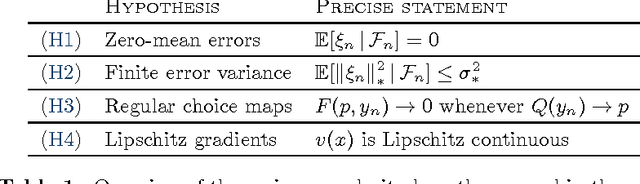
This paper examines the convergence of no-regret learning in games with continuous action sets. For concreteness, we focus on learning via "dual averaging", a widely used class of no-regret learning schemes where players take small steps along their individual payoff gradients and then "mirror" the output back to their action sets. In terms of feedback, we assume that players can only estimate their payoff gradients up to a zero-mean error with bounded variance. To study the convergence of the induced sequence of play, we introduce the notion of variational stability, and we show that stable equilibria are locally attracting with high probability whereas globally stable equilibria are globally attracting with probability 1. We also discuss some applications to mixed-strategy learning in finite games, and we provide explicit estimates of the method's convergence speed.