On the Foundation of Distributionally Robust Reinforcement Learning

Motivated by the need for a robust policy in the face of environment shifts between training and the deployment, we contribute to the theoretical foundation of distributionally robust reinforcement learning (DRRL). This is accomplished through a comprehensive modeling framework centered around distributionally robust Markov decision processes (DRMDPs). This framework obliges the decision maker to choose an optimal policy under the worst-case distributional shift orchestrated by an adversary. By unifying and extending existing formulations, we rigorously construct DRMDPs that embraces various modeling attributes for both the decision maker and the adversary. These attributes include adaptability granularity, exploring history-dependent, Markov, and Markov time-homogeneous decision maker and adversary dynamics. Additionally, we delve into the flexibility of shifts induced by the adversary, examining SA and S-rectangularity. Within this DRMDP framework, we investigate conditions for the existence or absence of the dynamic programming principle (DPP). From an algorithmic standpoint, the existence of DPP holds significant implications, as the vast majority of existing data and computationally efficiency RL algorithms are reliant on the DPP. To study its existence, we comprehensively examine combinations of controller and adversary attributes, providing streamlined proofs grounded in a unified methodology. We also offer counterexamples for settings in which a DPP with full generality is absent.

Adaptive, Doubly Optimal No-Regret Learning in Strongly Monotone and Exp-Concave Games with Gradient Feedback

Online gradient descent (OGD) is well known to be doubly optimal under strong convexity or monotonicity assumptions: (1) in the single-agent setting, it achieves an optimal regret of $\Theta(\log T)$ for strongly convex cost functions; and (2) in the multi-agent setting of strongly monotone games, with each agent employing OGD, we obtain last-iterate convergence of the joint action to a unique Nash equilibrium at an optimal rate of $\Theta(\frac{1}{T})$. While these finite-time guarantees highlight its merits, OGD has the drawback that it requires knowing the strong convexity/monotonicity parameters. In this paper, we design a fully adaptive OGD algorithm, \textsf{AdaOGD}, that does not require a priori knowledge of these parameters. In the single-agent setting, our algorithm achieves $O(\log^2(T))$ regret under strong convexity, which is optimal up to a log factor. Further, if each agent employs \textsf{AdaOGD} in strongly monotone games, the joint action converges in a last-iterate sense to a unique Nash equilibrium at a rate of $O(\frac{\log^3 T}{T})$, again optimal up to log factors. We illustrate our algorithms in a learning version of the classical newsvendor problem, where due to lost sales, only (noisy) gradient feedback can be observed. Our results immediately yield the first feasible and near-optimal algorithm for both the single-retailer and multi-retailer settings. We also extend our results to the more general setting of exp-concave cost functions and games, using the online Newton step (ONS) algorithm.

Sample Complexity of Variance-reduced Distributionally Robust Q-learning

Dynamic decision making under distributional shifts is of fundamental interest in theory and applications of reinforcement learning: The distribution of the environment on which the data is collected can differ from that of the environment on which the model is deployed. This paper presents two novel model-free algorithms, namely the distributionally robust Q-learning and its variance-reduced counterpart, that can effectively learn a robust policy despite distributional shifts. These algorithms are designed to efficiently approximate the $q$-function of an infinite-horizon $\gamma$-discounted robust Markov decision process with Kullback-Leibler uncertainty set to an entry-wise $\epsilon$-degree of precision. Further, the variance-reduced distributionally robust Q-learning combines the synchronous Q-learning with variance-reduction techniques to enhance its performance. Consequently, we establish that it attains a minmax sample complexity upper bound of $\tilde O(|S||A|(1-\gamma)^{-4}\epsilon^{-2})$, where $S$ and $A$ denote the state and action spaces. This is the first complexity result that is independent of the uncertainty size $\delta$, thereby providing new complexity theoretic insights. Additionally, a series of numerical experiments confirm the theoretical findings and the efficiency of the algorithms in handling distributional shifts.

Stochastic Nonsmooth Convex Optimization with Heavy-Tailed Noises

Recently, several studies consider the stochastic optimization problem but in a heavy-tailed noise regime, i.e., the difference between the stochastic gradient and the true gradient is assumed to have a finite $p$-th moment (say being upper bounded by $\sigma^{p}$ for some $\sigma\geq0$) where $p\in(1,2]$, which not only generalizes the traditional finite variance assumption ($p=2$) but also has been observed in practice for several different tasks. Under this challenging assumption, lots of new progress has been made for either convex or nonconvex problems, however, most of which only consider smooth objectives. In contrast, people have not fully explored and well understood this problem when functions are nonsmooth. This paper aims to fill this crucial gap by providing a comprehensive analysis of stochastic nonsmooth convex optimization with heavy-tailed noises. We revisit a simple clipping-based algorithm, whereas, which is only proved to converge in expectation but under the additional strong convexity assumption. Under appropriate choices of parameters, for both convex and strongly convex functions, we not only establish the first high-probability rates but also give refined in-expectation bounds compared with existing works. Remarkably, all of our results are optimal (or nearly optimal up to logarithmic factors) with respect to the time horizon $T$ even when $T$ is unknown in advance. Additionally, we show how to make the algorithm parameter-free with respect to $\sigma$, in other words, the algorithm can still guarantee convergence without any prior knowledge of $\sigma$.

A Finite Sample Complexity Bound for Distributionally Robust Q-learning

We consider a reinforcement learning setting in which the deployment environment is different from the training environment. Applying a robust Markov decision processes formulation, we extend the distributionally robust $Q$-learning framework studied in Liu et al. [2022]. Further, we improve the design and analysis of their multi-level Monte Carlo estimator. Assuming access to a simulator, we prove that the worst-case expected sample complexity of our algorithm to learn the optimal robust $Q$-function within an $\epsilon$ error in the sup norm is upper bounded by $\tilde O(|S||A|(1-\gamma)^{-5}\epsilon^{-2}p_{\wedge}^{-6}\delta^{-4})$, where $\gamma$ is the discount rate, $p_{\wedge}$ is the non-zero minimal support probability of the transition kernels and $\delta$ is the uncertainty size. This is the first sample complexity result for the model-free robust RL problem. Simulation studies further validate our theoretical results.

Breaking the Lower Bound with (Little) Structure: Acceleration in Non-Convex Stochastic Optimization with Heavy-Tailed Noise

We consider the stochastic optimization problem with smooth but not necessarily convex objectives in the heavy-tailed noise regime, where the stochastic gradient's noise is assumed to have bounded $p$th moment ($p\in(1,2]$). Zhang et al. (2020) is the first to prove the $\Omega(T^{\frac{1-p}{3p-2}})$ lower bound for convergence (in expectation) and provides a simple clipping algorithm that matches this optimal rate. Cutkosky and Mehta (2021) proposes another algorithm, which is shown to achieve the nearly optimal high-probability convergence guarantee $O(\log(T/\delta)T^{\frac{1-p}{3p-2}})$, where $\delta$ is the probability of failure. However, this desirable guarantee is only established under the additional assumption that the stochastic gradient itself is bounded in $p$th moment, which fails to hold even for quadratic objectives and centered Gaussian noise. In this work, we first improve the analysis of the algorithm in Cutkosky and Mehta (2021) to obtain the same nearly optimal high-probability convergence rate $O(\log(T/\delta)T^{\frac{1-p}{3p-2}})$, without the above-mentioned restrictive assumption. Next, and curiously, we show that one can achieve a faster rate than that dictated by the lower bound $\Omega(T^{\frac{1-p}{3p-2}})$ with only a tiny bit of structure, i.e., when the objective function $F(x)$ is assumed to be in the form of $\mathbb{E}_{\Xi\sim\mathcal{D}}[f(x,\Xi)]$, arguably the most widely applicable class of stochastic optimization problems. For this class of problems, we propose the first variance-reduced accelerated algorithm and establish that it guarantees a high-probability convergence rate of $O(\log(T/\delta)T^{\frac{1-p}{2p-1}})$ under a mild condition, which is faster than $\Omega(T^{\frac{1-p}{3p-2}})$. Notably, even when specialized to the finite-variance case, our result yields the (near-)optimal high-probability rate $O(\log(T/\delta)T^{-1/3})$.

Near-Optimal High-Probability Convergence for Non-Convex Stochastic Optimization with Variance Reduction

Traditional analyses for non-convex stochastic optimization problems characterize convergence bounds in expectation, which is inadequate as it does not supply a useful performance guarantee on a single run. Motivated by its importance, an emerging line of literature has recently studied the high-probability convergence behavior of several algorithms, including the classic stochastic gradient descent (SGD). However, no high-probability results are established for optimization algorithms with variance reduction, which is known to accelerate the convergence process and has been the de facto algorithmic technique for stochastic optimization at large. To close this important gap, we introduce a new variance-reduced algorithm for non-convex stochastic optimization, which we call Generalized SignSTORM. We show that with probability at least $1-\delta$, our algorithm converges at the rate of $O(\log(dT/\delta)/T^{1/3})$ after $T$ iterations where $d$ is the problem dimension. This convergence guarantee matches the existing lower bound up to a log factor, and to our best knowledge, is the first high-probability minimax (near-)optimal result. Finally, we demonstrate the effectiveness of our algorithm through numerical experiments.

Single-Trajectory Distributionally Robust Reinforcement Learning

As a framework for sequential decision-making, Reinforcement Learning (RL) has been regarded as an essential component leading to Artificial General Intelligence (AGI). However, RL is often criticized for having the same training environment as the test one, which also hinders its application in the real world. To mitigate this problem, Distributionally Robust RL (DRRL) is proposed to improve the worst performance in a set of environments that may contain the unknown test environment. Due to the nonlinearity of the robustness goal, most of the previous work resort to the model-based approach, learning with either an empirical distribution learned from the data or a simulator that can be sampled infinitely, which limits their applications in simple dynamics environments. In contrast, we attempt to design a DRRL algorithm that can be trained along a single trajectory, i.e., no repeated sampling from a state. Based on the standard Q-learning, we propose distributionally robust Q-learning with the single trajectory (DRQ) and its average-reward variant named differential DRQ. We provide asymptotic convergence guarantees and experiments for both settings, demonstrating their superiority in the perturbed environments against the non-robust ones.

Leveraging the Hints: Adaptive Bidding in Repeated First-Price Auctions

With the advent and increasing consolidation of e-commerce, digital advertising has very recently replaced traditional advertising as the main marketing force in the economy. In the past four years, a particularly important development in the digital advertising industry is the shift from second-price auctions to first-price auctions for online display ads. This shift immediately motivated the intellectually challenging question of how to bid in first-price auctions, because unlike in second-price auctions, bidding one's private value truthfully is no longer optimal. Following a series of recent works in this area, we consider a differentiated setup: we do not make any assumption about other bidders' maximum bid (i.e. it can be adversarial over time), and instead assume that we have access to a hint that serves as a prediction of other bidders' maximum bid, where the prediction is learned through some blackbox machine learning model. We consider two types of hints: one where a single point-prediction is available, and the other where a hint interval (representing a type of confidence region into which others' maximum bid falls) is available. We establish minimax optimal regret bounds for both cases and highlight the quantitatively different behavior between the two settings. We also provide improved regret bounds when the others' maximum bid exhibits the further structure of sparsity. Finally, we complement the theoretical results with demonstrations using real bidding data.

Distributionally Robust Offline Reinforcement Learning with Linear Function Approximation

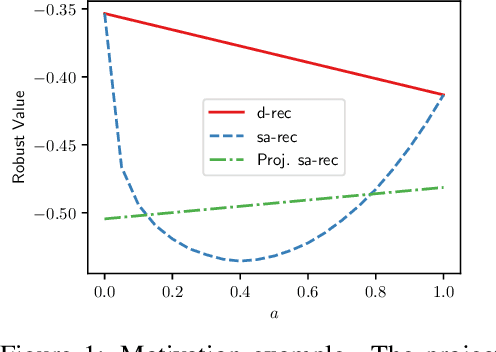
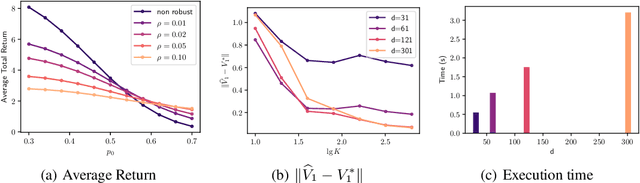
Among the reasons hindering reinforcement learning (RL) applications to real-world problems, two factors are critical: limited data and the mismatch between the testing environment (real environment in which the policy is deployed) and the training environment (e.g., a simulator). This paper attempts to address these issues simultaneously with distributionally robust offline RL, where we learn a distributionally robust policy using historical data obtained from the source environment by optimizing against a worst-case perturbation thereof. In particular, we move beyond tabular settings and consider linear function approximation. More specifically, we consider two settings, one where the dataset is well-explored and the other where the dataset has sufficient coverage. We propose two algorithms -- one for each of the two settings -- that achieve error bounds $\tilde{O}(d^{1/2}/N^{1/2})$ and $\tilde{O}(d^{3/2}/N^{1/2})$ respectively, where $d$ is the dimension in the linear function approximation and $N$ is the number of trajectories in the dataset. To the best of our knowledge, they provide the first non-asymptotic results of the sample complexity in this setting. Diverse experiments are conducted to demonstrate our theoretical findings, showing the superiority of our algorithm against the non-robust one.