MolBridge: Atom-Level Joint Graph Refinement for Robust Drug-Drug Interaction Event Prediction

Drug combinations offer therapeutic benefits but also carry the risk of adverse drug-drug interactions (DDIs), especially under complex molecular structures. Accurate DDI event prediction requires capturing fine-grained inter-drug relationships, which are critical for modeling metabolic mechanisms such as enzyme-mediated competition. However, existing approaches typically rely on isolated drug representations and fail to explicitly model atom-level cross-molecular interactions, limiting their effectiveness across diverse molecular complexities and DDI type distributions. To address these limitations, we propose MolBridge, a novel atom-level joint graph refinement framework for robust DDI event prediction. MolBridge constructs a joint graph that integrates atomic structures of drug pairs, enabling direct modeling of inter-drug associations. A central challenge in such joint graph settings is the potential loss of information caused by over-smoothing when modeling long-range atomic dependencies. To overcome this, we introduce a structure consistency module that iteratively refines node features while preserving the global structural context. This joint design allows MolBridge to effectively learn both local and global interaction outperforms state-of-the-art baselines, achieving superior performance across long-tail and inductive scenarios. patterns, yielding robust representations across both frequent and rare DDI types. Extensive experiments on two benchmark datasets show that MolBridge consistently. These results demonstrate the advantages of fine-grained graph refinement in improving the accuracy, robustness, and mechanistic interpretability of DDI event prediction.This work contributes to Web Mining and Content Analysis by developing graph-based methods for mining and analyzing drug-drug interaction networks.

Heavy-ball Algorithms Always Escape Saddle Points

Nonconvex optimization algorithms with random initialization have attracted increasing attention recently. It has been showed that many first-order methods always avoid saddle points with random starting points. In this paper, we answer a question: can the nonconvex heavy-ball algorithms with random initialization avoid saddle points? The answer is yes! Direct using the existing proof technique for the heavy-ball algorithms is hard due to that each iteration of the heavy-ball algorithm consists of current and last points. It is impossible to formulate the algorithms as iteration like xk+1= g(xk) under some mapping g. To this end, we design a new mapping on a new space. With some transfers, the heavy-ball algorithm can be interpreted as iterations after this mapping. Theoretically, we prove that heavy-ball gradient descent enjoys larger stepsize than the gradient descent to escape saddle points to escape the saddle point. And the heavy-ball proximal point algorithm is also considered; we also proved that the algorithm can always escape the saddle point.

Iteratively reweighted penalty alternating minimization methods with continuation for image deblurring

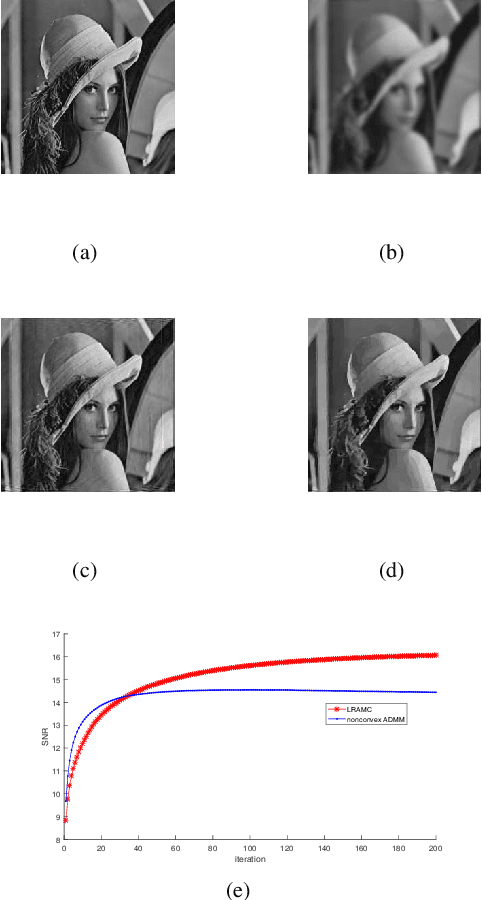
In this paper, we consider a class of nonconvex problems with linear constraints appearing frequently in the area of image processing. We solve this problem by the penalty method and propose the iteratively reweighted alternating minimization algorithm. To speed up the algorithm, we also apply the continuation strategy to the penalty parameter. A convergence result is proved for the algorithm. Compared with the nonconvex ADMM, the proposed algorithm enjoys both theoretical and computational advantages like weaker convergence requirements and faster speed. Numerical results demonstrate the efficiency of the proposed algorithm.