Maximum Entropy Inverse Reinforcement Learning of Diffusion Models with Energy-Based Models

We present a maximum entropy inverse reinforcement learning (IRL) approach for improving the sample quality of diffusion generative models, especially when the number of generation time steps is small. Similar to how IRL trains a policy based on the reward function learned from expert demonstrations, we train (or fine-tune) a diffusion model using the log probability density estimated from training data. Since we employ an energy-based model (EBM) to represent the log density, our approach boils down to the joint training of a diffusion model and an EBM. Our IRL formulation, named Diffusion by Maximum Entropy IRL (DxMI), is a minimax problem that reaches equilibrium when both models converge to the data distribution. The entropy maximization plays a key role in DxMI, facilitating the exploration of the diffusion model and ensuring the convergence of the EBM. We also propose Diffusion by Dynamic Programming (DxDP), a novel reinforcement learning algorithm for diffusion models, as a subroutine in DxMI. DxDP makes the diffusion model update in DxMI efficient by transforming the original problem into an optimal control formulation where value functions replace back-propagation in time. Our empirical studies show that diffusion models fine-tuned using DxMI can generate high-quality samples in as few as 4 and 10 steps. Additionally, DxMI enables the training of an EBM without MCMC, stabilizing EBM training dynamics and enhancing anomaly detection performance.

Kernel Metric Learning for In-Sample Off-Policy Evaluation of Deterministic RL Policies

We consider off-policy evaluation (OPE) of deterministic target policies for reinforcement learning (RL) in environments with continuous action spaces. While it is common to use importance sampling for OPE, it suffers from high variance when the behavior policy deviates significantly from the target policy. In order to address this issue, some recent works on OPE proposed in-sample learning with importance resampling. Yet, these approaches are not applicable to deterministic target policies for continuous action spaces. To address this limitation, we propose to relax the deterministic target policy using a kernel and learn the kernel metrics that minimize the overall mean squared error of the estimated temporal difference update vector of an action value function, where the action value function is used for policy evaluation. We derive the bias and variance of the estimation error due to this relaxation and provide analytic solutions for the optimal kernel metric. In empirical studies using various test domains, we show that the OPE with in-sample learning using the kernel with optimized metric achieves significantly improved accuracy than other baselines.

Generalized Contrastive Divergence: Joint Training of Energy-Based Model and Diffusion Model through Inverse Reinforcement Learning

We present Generalized Contrastive Divergence (GCD), a novel objective function for training an energy-based model (EBM) and a sampler simultaneously. GCD generalizes Contrastive Divergence (Hinton, 2002), a celebrated algorithm for training EBM, by replacing Markov Chain Monte Carlo (MCMC) distribution with a trainable sampler, such as a diffusion model. In GCD, the joint training of EBM and a diffusion model is formulated as a minimax problem, which reaches an equilibrium when both models converge to the data distribution. The minimax learning with GCD bears interesting equivalence to inverse reinforcement learning, where the energy corresponds to a negative reward, the diffusion model is a policy, and the real data is expert demonstrations. We present preliminary yet promising results showing that joint training is beneficial for both EBM and a diffusion model. GCD enables EBM training without MCMC while improving the sample quality of a diffusion model.

Variational Weighting for Kernel Density Ratios

Kernel density estimation (KDE) is integral to a range of generative and discriminative tasks in machine learning. Drawing upon tools from the multidimensional calculus of variations, we derive an optimal weight function that reduces bias in standard kernel density estimates for density ratios, leading to improved estimates of prediction posteriors and information-theoretic measures. In the process, we shed light on some fundamental aspects of density estimation, particularly from the perspective of algorithms that employ KDEs as their main building blocks.

Energy-Based Models for Anomaly Detection: A Manifold Diffusion Recovery Approach

We present a new method of training energy-based models (EBMs) for anomaly detection that leverages low-dimensional structures within data. The proposed algorithm, Manifold Projection-Diffusion Recovery (MPDR), first perturbs a data point along a low-dimensional manifold that approximates the training dataset. Then, EBM is trained to maximize the probability of recovering the original data. The training involves the generation of negative samples via MCMC, as in conventional EBM training, but from a different distribution concentrated near the manifold. The resulting near-manifold negative samples are highly informative, reflecting relevant modes of variation in data. An energy function of MPDR effectively learns accurate boundaries of the training data distribution and excels at detecting out-of-distribution samples. Experimental results show that MPDR exhibits strong performance across various anomaly detection tasks involving diverse data types, such as images, vectors, and acoustic signals.

Local Metric Learning for Off-Policy Evaluation in Contextual Bandits with Continuous Actions

We consider local kernel metric learning for off-policy evaluation (OPE) of deterministic policies in contextual bandits with continuous action spaces. Our work is motivated by practical scenarios where the target policy needs to be deterministic due to domain requirements, such as prescription of treatment dosage and duration in medicine. Although importance sampling (IS) provides a basic principle for OPE, it is ill-posed for the deterministic target policy with continuous actions. Our main idea is to relax the target policy and pose the problem as kernel-based estimation, where we learn the kernel metric in order to minimize the overall mean squared error (MSE). We present an analytic solution for the optimal metric, based on the analysis of bias and variance. Whereas prior work has been limited to scalar action spaces or kernel bandwidth selection, our work takes a step further being capable of vector action spaces and metric optimization. We show that our estimator is consistent, and significantly reduces the MSE compared to baseline OPE methods through experiments on various domains.

Evaluating Out-of-Distribution Detectors Through Adversarial Generation of Outliers

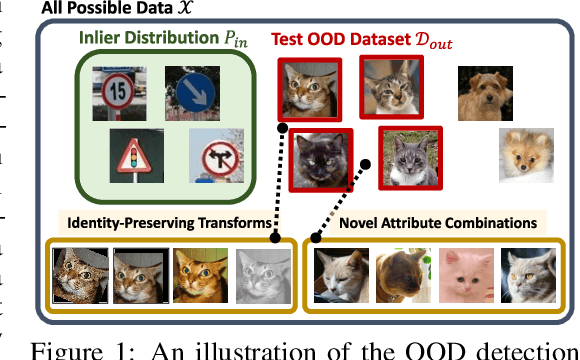
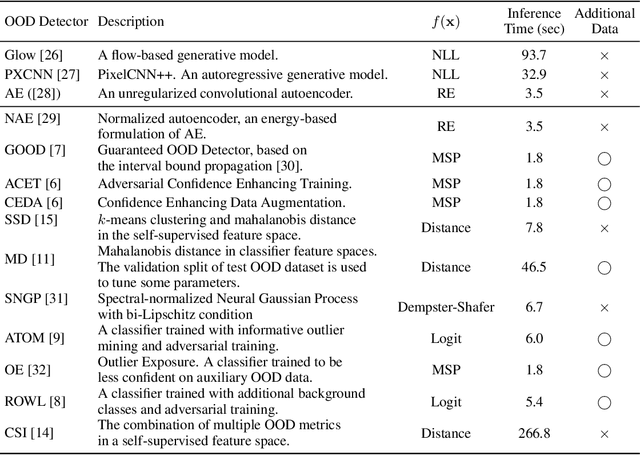
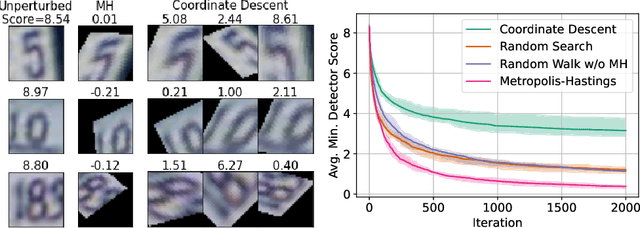
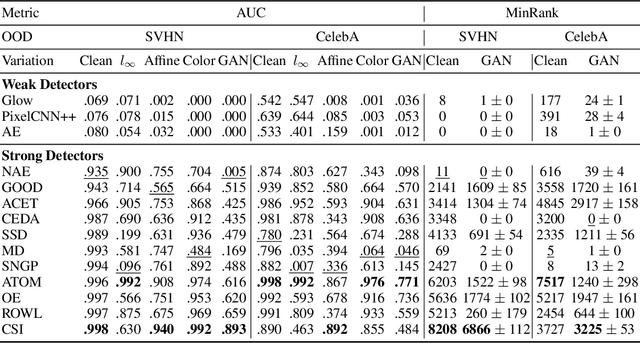
A reliable evaluation method is essential for building a robust out-of-distribution (OOD) detector. Current robustness evaluation protocols for OOD detectors rely on injecting perturbations to outlier data. However, the perturbations are unlikely to occur naturally or not relevant to the content of data, providing a limited assessment of robustness. In this paper, we propose Evaluation-via-Generation for OOD detectors (EvG), a new protocol for investigating the robustness of OOD detectors under more realistic modes of variation in outliers. EvG utilizes a generative model to synthesize plausible outliers, and employs MCMC sampling to find outliers misclassified as in-distribution with the highest confidence by a detector. We perform a comprehensive benchmark comparison of the performance of state-of-the-art OOD detectors using EvG, uncovering previously overlooked weaknesses.

Autoencoding Under Normalization Constraints

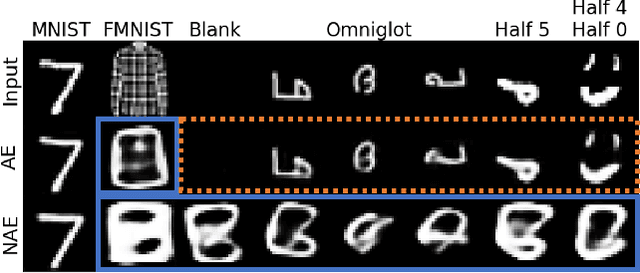
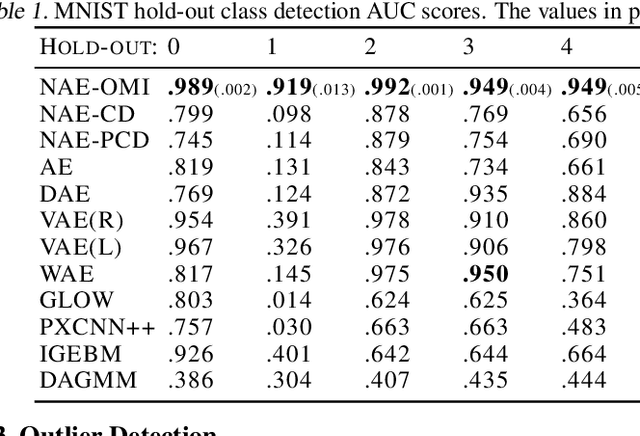
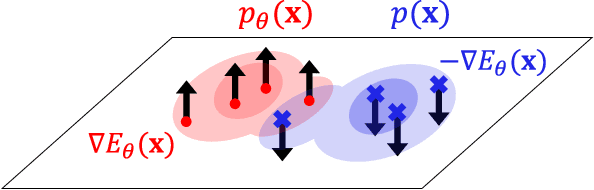
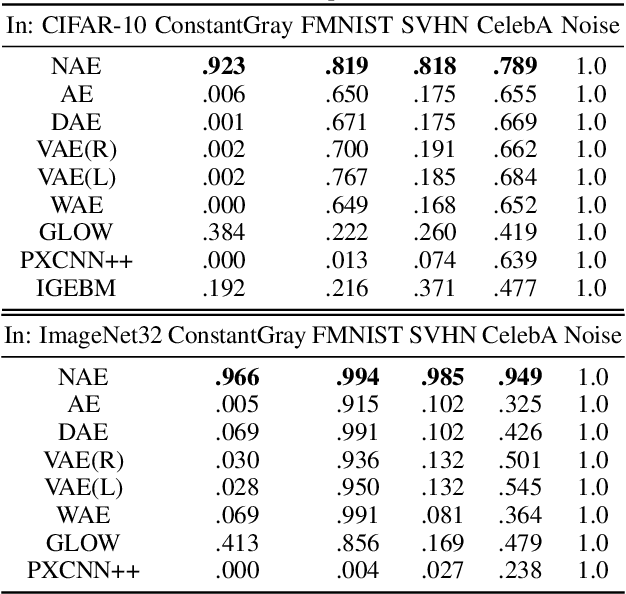
Likelihood is a standard estimate for outlier detection. The specific role of the normalization constraint is to ensure that the out-of-distribution (OOD) regime has a small likelihood when samples are learned using maximum likelihood. Because autoencoders do not possess such a process of normalization, they often fail to recognize outliers even when they are obviously OOD. We propose the Normalized Autoencoder (NAE), a normalized probabilistic model constructed from an autoencoder. The probability density of NAE is defined using the reconstruction error of an autoencoder, which is differently defined in the conventional energy-based model. In our model, normalization is enforced by suppressing the reconstruction of negative samples, significantly improving the outlier detection performance. Our experimental results confirm the efficacy of NAE, both in detecting outliers and in generating in-distribution samples.

Learning to increase matching efficiency in identifying additional b-jets in the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process

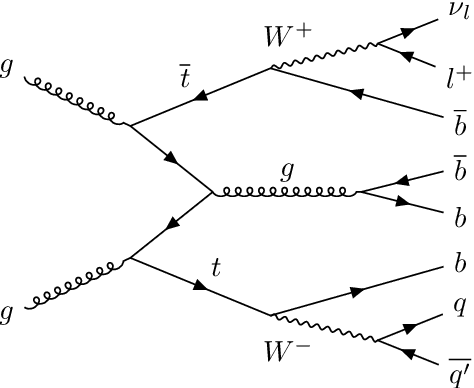
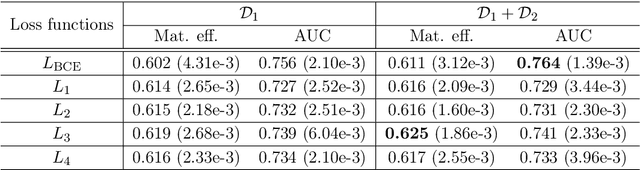
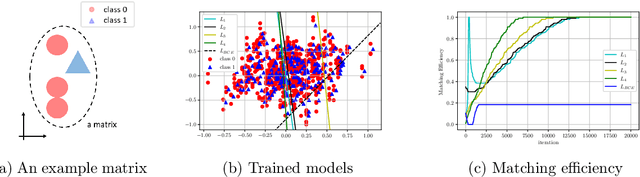
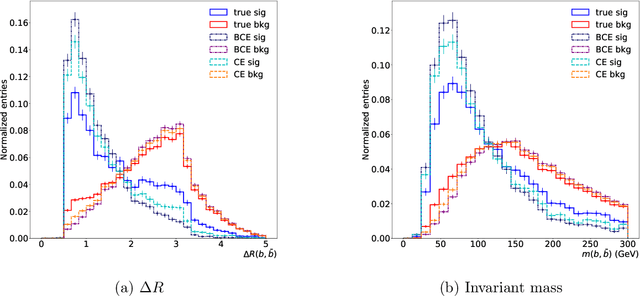
The $\text{t}\bar{\text{t}}\text{H}(\text{b}\bar{\text{b}})$ process is an essential channel to reveal the Higgs properties but has an irreducible background from the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process, which produces a top quark pair in association with a b quark pair. Therefore, understanding the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process is crucial for improving the sensitivity of a search for the $\text{t}\bar{\text{t}}\text{H}(\text{b}\bar{\text{b}})$ process. To this end, when measuring the differential cross-section of the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ process, we need to distinguish the b-jets originated from top quark decays, and additional b-jets originated from gluon splitting. Since there are no simple identification rules, we adopt deep learning methods to learn from data to identify the additional b-jets from the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ events. Specifically, by exploiting the special structure of the $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ event data, we propose several loss functions that can be minimized to directly increase the matching efficiency, the accuracy of identifying additional b-jets. We discuss the difference between our method and another deep learning-based approach based on binary classification arXiv:1910.14535 using synthetic data. We then verify that additional b-jets can be identified more accurately by increasing matching efficiency directly rather than the binary classification accuracy, using simulated $\text{t}\bar{\text{t}}\text{b}\bar{\text{b}}$ event data in the lepton+jets channel from pp collision at $\sqrt{s}$ = 13 TeV.

K-Beam Minimax: Efficient Optimization for Deep Adversarial Learning

Minimax optimization plays a key role in adversarial training of machine learning algorithms, such as learning generative models, domain adaptation, privacy preservation, and robust learning. In this paper, we demonstrate the failure of alternating gradient descent in minimax optimization problems due to the discontinuity of solutions of the inner maximization. To address this, we propose a new epsilon-subgradient descent algorithm that addresses this problem by simultaneously tracking K candidate solutions. Practically, the algorithm can find solutions that previous saddle-point algorithms cannot find, with only a sublinear increase of complexity in K. We analyze the conditions under which the algorithm converges to the true solution in detail. A significant improvement in stability and convergence speed of the algorithm is observed in simple representative problems, GAN training, and domain-adaptation problems.