Historical Review of Variants of Informal Semantics for Logic Programs under Answer Set Semantics: GL'88, GL'91, GK'14, D-V'12

This note presents a historical survey of informal semantics that are associated with logic programming under answer set semantics. We review these in uniform terms and align them with two paradigms: Answer Set Programming and ASP-Prolog -- two prominent Knowledge Representation and Reasoning Paradigms in Artificial Intelligence. Under consideration in Theory and Practice of Logic Programming (TPLP).

Elementary Sets for Logic Programs

By introducing the concepts of a loop and a loop formula, Lin and Zhao showed that the answer sets of a nondisjunctive logic program are exactly the models of its Clark's completion that satisfy the loop formulas of all loops. Recently, Gebser and Schaub showed that the Lin-Zhao theorem remains correct even if we restrict loop formulas to a special class of loops called ``elementary loops.'' In this paper, we simplify and generalize the notion of an elementary loop, and clarify its role. We propose the notion of an elementary set, which is almost equivalent to the notion of an elementary loop for nondisjunctive programs, but is simpler, and, unlike elementary loops, can be extended to disjunctive programs without producing unintuitive results. We show that the maximal unfounded elementary sets for the ``relevant'' part of a program are exactly the minimal sets among the nonempty unfounded sets. We also present a graph-theoretic characterization of elementary sets for nondisjunctive programs, which is simpler than the one proposed in (Gebser & Schaub 2005). Unlike the case of nondisjunctive programs, we show that the problem of deciding an elementary set is coNP-complete for disjunctive programs.

System Predictor: Grounding Size Estimator for Logic Programs under Answer Set Semantics

Answer set programming is a declarative logic programming paradigm geared towards solving difficult combinatorial search problems. While different logic programs can encode the same problem, their performance may vary significantly. It is not always easy to identify which version of the program performs the best. We present the system Predictor (and its algorithmic backend) for estimating the grounding size of programs, a metric that can influence a performance of a system processing a program. We evaluate the impact of Predictor when used as a guide for rewritings produced by the answer set programming rewriting tools Projector and Lpopt. The results demonstrate potential to this approach.

Proceedings 38th International Conference on Logic Programming

ICLP is the premier international event for presenting research in logic programming. Contributions to ICLP 2022 were sought in all areas of logic programming, including but not limited to: Foundations: Semantics, Formalisms, Nonmonotonic reasoning, Knowledge representation. Languages issues: Concurrency, Objects, Coordination, Mobility, Higher order, Types, Modes, Assertions, Modules, Meta-programming, Logic-based domain-specific languages, Programming techniques. Programming support: Program analysis, Transformation, Validation, Verification, Debugging, Profiling, Testing, Execution visualization. Implementation: Compilation, Virtual machines, Memory management, Parallel and Distributed execution, Constraint handling rules, Tabling, Foreign interfaces, User interfaces. Related Paradigms and Synergies: Inductive and coinductive logic programming, Constraint logic programming, Answer set programming, Interaction with SAT, SMT and CSP solvers, Theorem proving, Argumentation, Probabilistic programming, Machine learning. Applications: Databases, Big data, Data integration and federation, Software engineering, Natural language processing, Web and semantic web, Agents, Artificial intelligence, Computational life sciences, Cyber-security, Robotics, Education.

Unifying Framework for Optimizations in non-boolean Formalisms

Search-optimization problems are plentiful in scientific and engineering domains. Artificial intelligence has long contributed to the development of search algorithms and declarative programming languages geared towards solving and modeling search-optimization problems. Automated reasoning and knowledge representation are the subfields of AI that are particularly vested in these developments. Many popular automated reasoning paradigms provide users with languages supporting optimization statements. Recall integer linear programming, MaxSAT, optimization satisfiability modulo theory, and (constraint) answer set programming. These paradigms vary significantly in their languages in ways they express quality conditions on computed solutions. Here we propose a unifying framework of so called extended weight systems that eliminates syntactic distinctions between paradigms. They allow us to see essential similarities and differences between optimization statements provided by distinct automated reasoning languages. We also study formal properties of the proposed systems that immediately translate into formal properties of paradigms that can be captured within our framework. Under consideration in Theory and Practice of Logic Programming (TPLP).

An Abstract View on Optimizations in Propositional Frameworks

Search-optimization problems are plentiful in scientific and engineering domains. Artificial intelligence has long contributed to the development of search algorithms and declarative programming languages geared towards solving and modeling search-optimization problems. Automated reasoning and knowledge representation are the subfields of AI that are particularly vested in these developments. Many popular automated reasoning paradigms provide users with languages supporting optimization statements: MaxSAT or answer set programming, to name a few. These paradigms vary significantly in their languages and in the ways they express quality conditions on computed solutions. Here we propose a unifying framework of so-called weight systems that eliminates syntactic distinctions between paradigms and allows us to see essential similarities and differences between optimization statements provided by paradigms. This unifying outlook has a significant simplifying and explanatory potential in the studies of optimization and modularity in automated reasoning and knowledge representation providing technical means for bridging distinct formalisms and developing translational solvers. Under consideration in Theory and Practice of Logic Programming (TPLP).

Constraint Answer Set Programming: Integrational and Translational (or SMT-based) Approaches

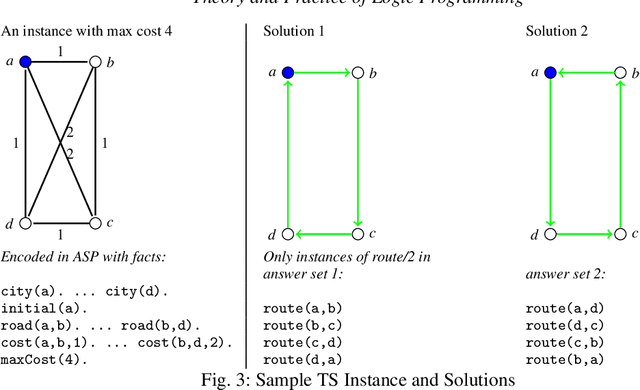
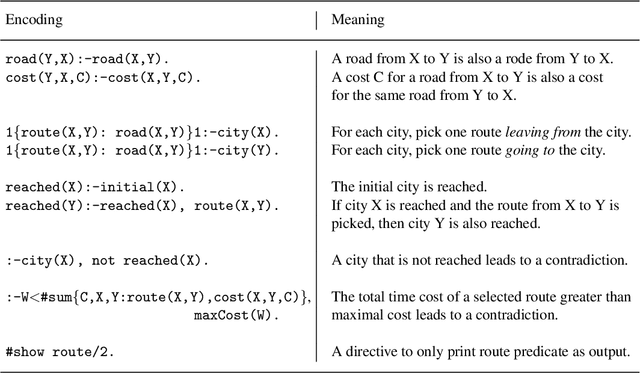
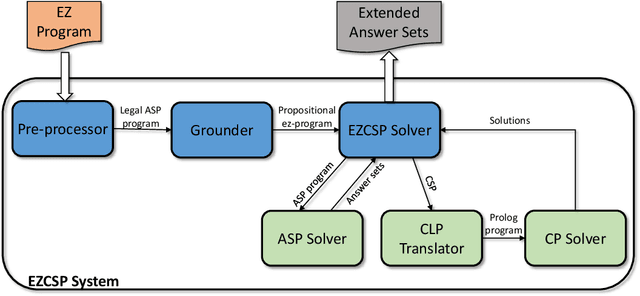
Constraint answer set programming or CASP, for short, is a hybrid approach in automated reasoning putting together the advances of distinct research areas such as answer set programming, constraint processing, and satisfiability modulo theories. Constraint answer set programming demonstrates promising results, including the development of a multitude of solvers: acsolver, clingcon, ezcsp, idp, inca, dingo, mingo, aspmt, clingo[l,dl], and ezsmt. It opens new horizons for declarative programming applications such as solving complex train scheduling problems. Systems designed to find solutions to constraint answer set programs can be grouped according to their construction into, what we call, integrational or translational approaches. The focus of this paper is an overview of the key ingredients of the design of constraint answer set solvers drawing distinctions and parallels between integrational and translational approaches. The paper also provides a glimpse at the kind of programs its users develop by utilizing a CASP encoding of Travelling Salesman problem for illustration. In addition, we place the CASP technology on the map among its automated reasoning peers as well as discuss future possibilities for the development of CASP.

Modular Answer Set Programming as a Formal Specification Language

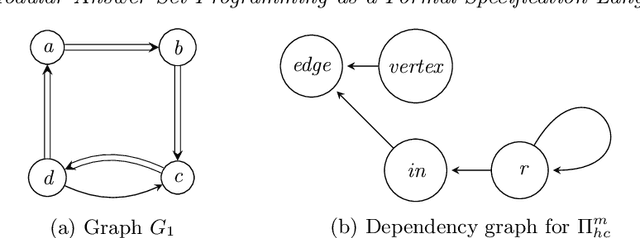
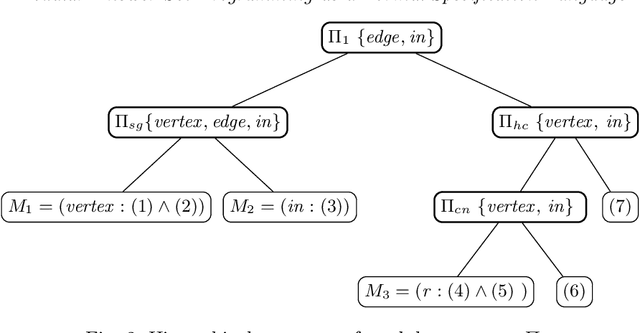
In this paper, we study the problem of formal verification for Answer Set Programming (ASP), namely, obtaining a formal proof showing that the answer sets of a given (non-ground) logic program P correctly correspond to the solutions to the problem encoded by P, regardless of the problem instance. To this aim, we use a formal specification language based on ASP modules, so that each module can be proved to capture some informal aspect of the problem in an isolated way. This specification language relies on a novel definition of (possibly nested, first order) program modules that may incorporate local hidden atoms at different levels. Then, verifying the logic program P amounts to prove some kind of equivalence between P and its modular specification. Under consideration for acceptance in TPLP.

Information Extraction Tool Text2ALM: From Narratives to Action Language System Descriptions

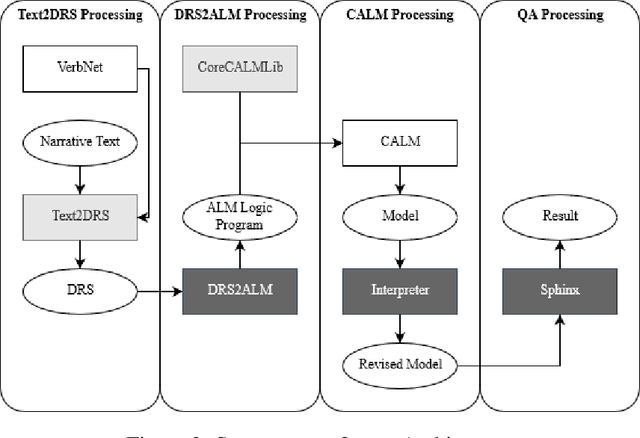
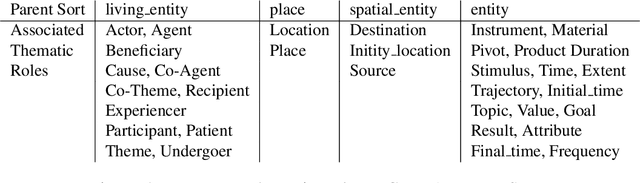
In this work we design a narrative understanding tool Text2ALM. This tool uses an action language ALM to perform inferences on complex interactions of events described in narratives. The methodology used to implement the Text2ALM system was originally outlined by Lierler, Inclezan, and Gelfond (2017) via a manual process of converting a narrative to an ALM model. It relies on a conglomeration of resources and techniques from two distinct fields of artificial intelligence, namely, natural language processing and knowledge representation and reasoning. The effectiveness of system Text2ALM is measured by its ability to correctly answer questions from the bAbI tasks published by Facebook Research in 2015. This tool matched or exceeded the performance of state-of-the-art machine learning methods in six of the seven tested tasks. We also illustrate that the Text2ALM approach generalizes to a broader spectrum of narratives.

SMT-based Constraint Answer Set Solver EZSMT+

Constraint answer set programming integrates answer set programming with constraint processing. System EZSMT+ is a constraint answer set programming tool that utilizes satisfiability modulo theory solvers for search. Its theoretical foundation lies on generalizations of Niemela's characterization of answer sets of a logic program via so called level rankings.