Pedro Cabalar
University of Coruña
Compiling Metric Temporal Answer Set Programming
Jun 09, 2025Abstract:We develop a computational approach to Metric Answer Set Programming (ASP) to allow for expressing quantitative temporal constrains, like durations and deadlines. A central challenge is to maintain scalability when dealing with fine-grained timing constraints, which can significantly exacerbate ASP's grounding bottleneck. To address this issue, we leverage extensions of ASP with difference constraints, a simplified form of linear constraints, to handle time-related aspects externally. Our approach effectively decouples metric ASP from the granularity of time, resulting in a solution that is unaffected by time precision.
Proceedings 40th International Conference on Logic Programming
Feb 11, 2025Abstract:Since the first conference In Marseille in 1982, the International Conference on Logic Programming (ICLP) has been the premier international event for presenting research in logic programming. These proceedings include technical communications about, and abstracts for presentations given at the 40th ICLP held October 14-17, in Dallas Texas, USA. The papers and abstracts in this volume include the following areas and topics. Formal and operational semantics: including non-monotonic reasoning, probabilistic reasoning, argumentation, and semantic issues of combining logic with neural models. Language design and programming methodologies such as answer set programming. inductive logic programming, and probabilistic programming. Program analysis and logic-based validation of generated programs. Implementation methodologies including constraint implementation, tabling, Logic-based prompt engineering, and the interaction of logic programming with LLMs.
Strong Equivalence in Answer Set Programming with Constraints
Feb 06, 2025Abstract:We investigate the concept of strong equivalence within the extended framework of Answer Set Programming with constraints. Two groups of rules are considered strongly equivalent if, informally speaking, they have the same meaning in any context. We demonstrate that, under certain assumptions, strong equivalence between rule sets in this extended setting can be precisely characterized by their equivalence in the logic of Here-and-There with constraints. Furthermore, we present a translation from the language of several clingo-based answer set solvers that handle constraints into the language of Here-and-There with constraints. This translation enables us to leverage the logic of Here-and-There to reason about strong equivalence within the context of these solvers. We also explore the computational complexity of determining strong equivalence in this context.
Metric Dynamic Equilibrium Logic
Jan 19, 2024Abstract:In temporal extensions of Answer Set Programming (ASP) based on linear-time, the behavior of dynamic systems is captured by sequences of states. While this representation reflects their relative order, it abstracts away the specific times associated with each state. In many applications, however, timing constraints are important like, for instance, when planning and scheduling go hand in hand. We address this by developing a metric extension of linear-time Dynamic Equilibrium Logic, in which dynamic operators are constrained by intervals over integers. The resulting Metric Dynamic Equilibrium Logic provides the foundation of an ASP-based approach for specifying qualitative and quantitative dynamic constraints. As such, it constitutes the most general among a whole spectrum of temporal extensions of Equilibrium Logic. In detail, we show that it encompasses Temporal, Dynamic, Metric, and regular Equilibrium Logic, as well as its classic counterparts once the law of the excluded middle is added.
Past-present temporal programs over finite traces
Jul 24, 2023Abstract:Extensions of Answer Set Programming with language constructs from temporal logics, such as temporal equilibrium logic over finite traces (TELf), provide an expressive computational framework for modeling dynamic applications. In this paper, we study the so-called past-present syntactic subclass, which consists of a set of logic programming rules whose body references to the past and head to the present. Such restriction ensures that the past remains independent of the future, which is the case in most dynamic domains. We extend the definitions of completion and loop formulas to the case of past-present formulas, which allows capturing the temporal stable models of a set of past-present temporal programs by means of an LTLf expression.
Metric Temporal Equilibrium Logic over Timed Traces
Apr 28, 2023Abstract:In temporal extensions of Answer Set Programming (ASP) based on linear-time, the behavior of dynamic systems is captured by sequences of states. While this representation reflects their relative order, it abstracts away the specific times associated with each state. However, timing constraints are important in many applications like, for instance, when planning and scheduling go hand in hand. We address this by developing a metric extension of linear-time temporal equilibrium logic, in which temporal operators are constrained by intervals over natural numbers. The resulting Metric Equilibrium Logic provides the foundation of an ASP-based approach for specifying qualitative and quantitative dynamic constraints. To this end, we define a translation of metric formulas into monadic first-order formulas and give a correspondence between their models in Metric Equilibrium Logic and Monadic Quantified Equilibrium Logic, respectively. Interestingly, our translation provides a blue print for implementation in terms of ASP modulo difference constraints.
Explainable Machine Larning for liver transplantation
Sep 28, 2021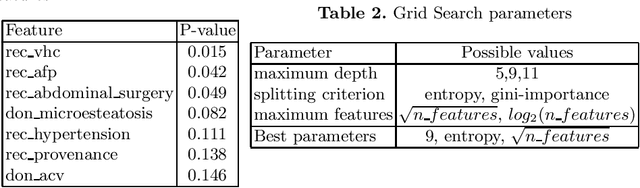
Abstract:In this work, we present a flexible method for explaining, in human readable terms, the predictions made by decision trees used as decision support in liver transplantation. The decision trees have been obtained through machine learning applied on a dataset collected at the liver transplantation unit at the Coru\~na University Hospital Center and are used to predict long term (five years) survival after transplantation. The method we propose is based on the representation of the decision tree as a set of rules in a logic program (LP) that is further annotated with text messages. This logic program is then processed using the tool xclingo (based on Answer Set Programming) that allows building compound explanations depending on the annotation text and the rules effectively fired when a given input is provided. We explore two alternative LP encodings: one in which rules respect the tree structure (more convenient to reflect the learning process) and one where each rule corresponds to a (previously simplified) tree path (more readable for decision making).
Automata for dynamic answer set solving: Preliminary report
Sep 04, 2021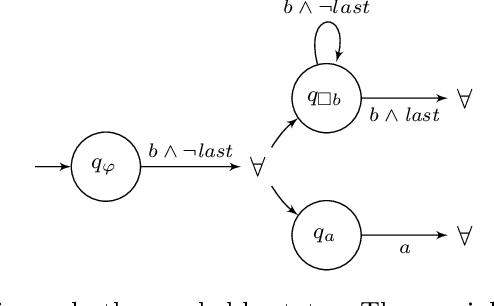


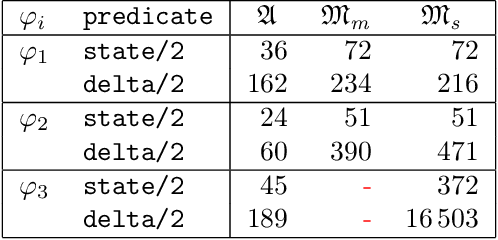
Abstract:We explore different ways of implementing temporal constraints expressed in an extension of Answer Set Programming (ASP) with language constructs from dynamic logic. Foremost, we investigate how automata can be used for enforcing such constraints. The idea is to transform a dynamic constraint into an automaton expressed in terms of a logic program that enforces the satisfaction of the original constraint. What makes this approach attractive is its independence of time stamps and the potential to detect unsatisfiability. On the one hand, we elaborate upon a transformation of dynamic formulas into alternating automata that relies on meta-programming in ASP. This is the first application of reification applied to theory expressions in gringo. On the other hand, we propose two transformations of dynamic formulas into monadic second-order formulas. These can then be used by off-the-shelf tools to construct the corresponding automata. We contrast both approaches empirically with the one of the temporal ASP solver telingo that directly maps dynamic constraints to logic programs. Since this preliminary study is restricted to dynamic formulas in integrity constraints, its implementations and (empirical) results readily apply to conventional linear dynamic logic, too.
Towards a Semantics for Hybrid ASP systems
Aug 06, 2021Abstract:Over the last decades the development of ASP has brought about an expressive modeling language powered by highly performant systems. At the same time, it gets more and more difficult to provide semantic underpinnings capturing the resulting constructs and inferences. This is even more severe when it comes to hybrid ASP languages and systems that are often needed to handle real-world applications. We address this challenge and introduce the concept of abstract and structured theories that allow us to formally elaborate upon their integration with ASP. We then use this concept to make precise the semantic characterization of CLINGO's theory-reasoning framework and establish its correspondence to the logic of Here-and-there with constraints. This provides us with a formal framework in which we can elaborate formal properties of existing hybridizations of CLINGO such as CLINGCON, CLINGOM[DL], and CLINGO[LP].
Multi-Context Systems: Dynamics and Evolution (Pre-Print of "Multi-context systems in dynamic environments")
Jun 12, 2021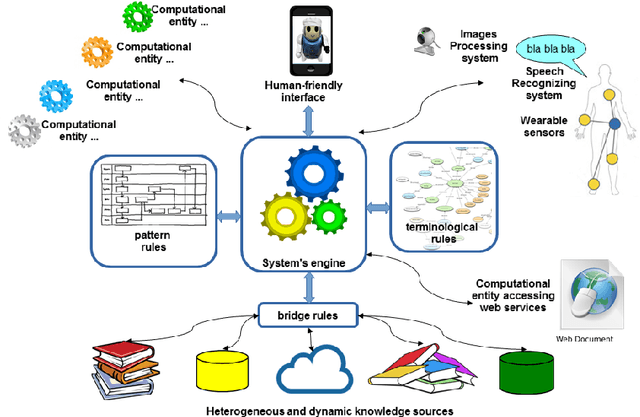
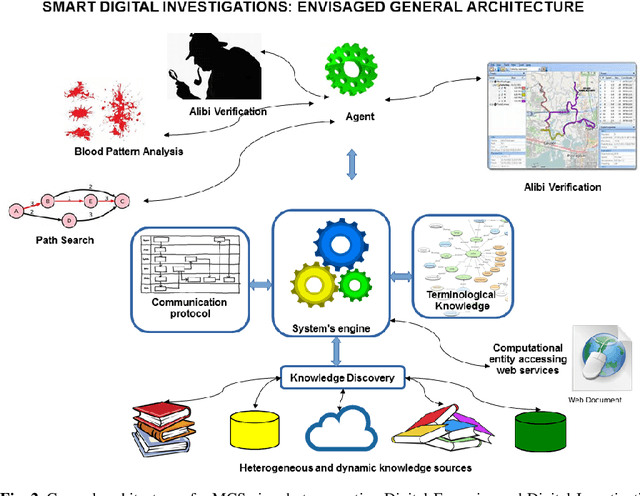
Abstract:Multi-Context Systems (MCS) model in Computational Logic distributed systems composed of heterogeneous sources, or "contexts", interacting via special rules called "bridge rules". In this paper, we consider how to enhance flexibility and generality in bridge-rules definition and application. In particular, we introduce and discuss some formal extensions of MCSs useful for a practical use in dynamic environments, and we try to provide guidelines for implementations
* 35 pages 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge