Transformers Meet In-Context Learning: A Universal Approximation Theory

Modern large language models are capable of in-context learning, the ability to perform new tasks at inference time using only a handful of input-output examples in the prompt, without any fine-tuning or parameter updates. We develop a universal approximation theory to better understand how transformers enable in-context learning. For any class of functions (each representing a distinct task), we demonstrate how to construct a transformer that, without any further weight updates, can perform reliable prediction given only a few in-context examples. In contrast to much of the recent literature that frames transformers as algorithm approximators -- i.e., constructing transformers to emulate the iterations of optimization algorithms as a means to approximate solutions of learning problems -- our work adopts a fundamentally different approach rooted in universal function approximation. This alternative approach offers approximation guarantees that are not constrained by the effectiveness of the optimization algorithms being approximated, thereby extending far beyond convex problems and linear function classes. Our construction sheds light on how transformers can simultaneously learn general-purpose representations and adapt dynamically to in-context examples.

Provable Efficiency of Guidance in Diffusion Models for General Data Distribution

Diffusion models have emerged as a powerful framework for generative modeling, with guidance techniques playing a crucial role in enhancing sample quality. Despite their empirical success, a comprehensive theoretical understanding of the guidance effect remains limited. Existing studies only focus on case studies, where the distribution conditioned on each class is either isotropic Gaussian or supported on a one-dimensional interval with some extra conditions. How to analyze the guidance effect beyond these case studies remains an open question. Towards closing this gap, we make an attempt to analyze diffusion guidance under general data distributions. Rather than demonstrating uniform sample quality improvement, which does not hold in some distributions, we prove that guidance can improve the whole sample quality, in the sense that the average reciprocal of the classifier probability decreases with the existence of guidance. This aligns with the motivation of introducing guidance.

Minimax-Optimal Multi-Agent Robust Reinforcement Learning

Multi-agent robust reinforcement learning, also known as multi-player robust Markov games (RMGs), is a crucial framework for modeling competitive interactions under environmental uncertainties, with wide applications in multi-agent systems. However, existing results on sample complexity in RMGs suffer from at least one of three obstacles: restrictive range of uncertainty level or accuracy, the curse of multiple agents, and the barrier of long horizons, all of which cause existing results to significantly exceed the information-theoretic lower bound. To close this gap, we extend the Q-FTRL algorithm \citep{li2022minimax} to the RMGs in finite-horizon setting, assuming access to a generative model. We prove that the proposed algorithm achieves an $\varepsilon$-robust coarse correlated equilibrium (CCE) with a sample complexity (up to log factors) of $\widetilde{O}\left(H^3S\sum_{i=1}^mA_i\min\left\{H,1/R\right\}/\varepsilon^2\right)$, where $S$ denotes the number of states, $A_i$ is the number of actions of the $i$-th agent, $H$ is the finite horizon length, and $R$ is uncertainty level. We also show that this sample compelxity is minimax optimal by combining an information-theoretic lower bound. Additionally, in the special case of two-player zero-sum RMGs, the algorithm achieves an $\varepsilon$-robust Nash equilibrium (NE) with the same sample complexity.

Improved Convergence Rate for Diffusion Probabilistic Models

Score-based diffusion models have achieved remarkable empirical performance in the field of machine learning and artificial intelligence for their ability to generate high-quality new data instances from complex distributions. Improving our understanding of diffusion models, including mainly convergence analysis for such models, has attracted a lot of interests. Despite a lot of theoretical attempts, there still exists significant gap between theory and practice. Towards to close this gap, we establish an iteration complexity at the order of $d^{1/3}\varepsilon^{-2/3}$, which is better than $d^{5/12}\varepsilon^{-1}$, the best known complexity achieved before our work. This convergence analysis is based on a randomized midpoint method, which is first proposed for log-concave sampling (Shen and Lee, 2019), and then extended to diffusion models by Gupta et al. (2024). Our theory accommodates $\varepsilon$-accurate score estimates, and does not require log-concavity on the target distribution. Moreover, the algorithm can also be parallelized to run in only $O(\log^2(d/\varepsilon))$ parallel rounds in a similar way to prior works.

Compressed Subspace Learning Based on Canonical Angle Preserving Property

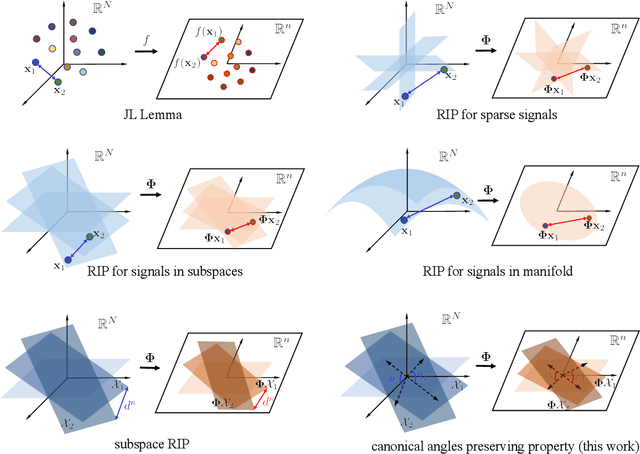
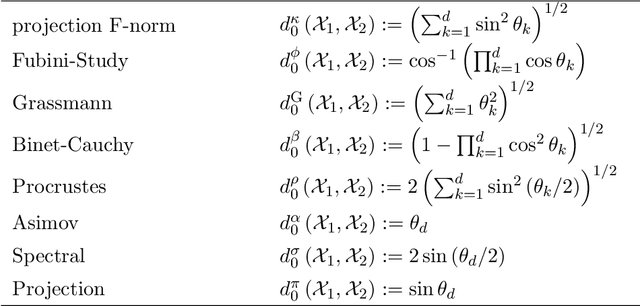
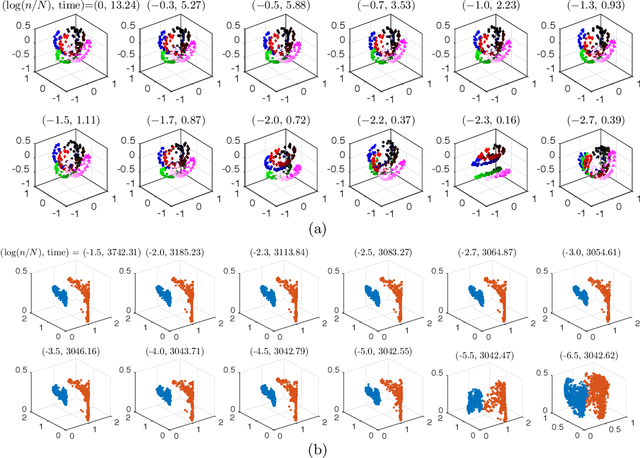
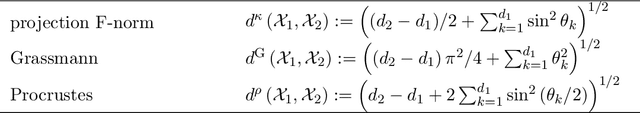
Union of Subspaces (UoS) is a popular model to describe the underlying low-dimensional structure of data. The fine details of UoS structure can be described in terms of canonical angles (also known as principal angles) between subspaces, which is a well-known characterization for relative subspace positions. In this paper, we prove that random projection with the so-called Johnson-Lindenstrauss (JL) property approximately preserves canonical angles between subspaces with overwhelming probability. This result indicates that random projection approximately preserves the UoS structure. Inspired by this result, we propose a framework of Compressed Subspace Learning (CSL), which enables to extract useful information from the UoS structure of data in a greatly reduced dimension. We demonstrate the effectiveness of CSL in various subspace-related tasks such as subspace visualization, active subspace detection, and subspace clustering.

Linear Convergence of An Iterative Phase Retrieval Algorithm with Data Reuse

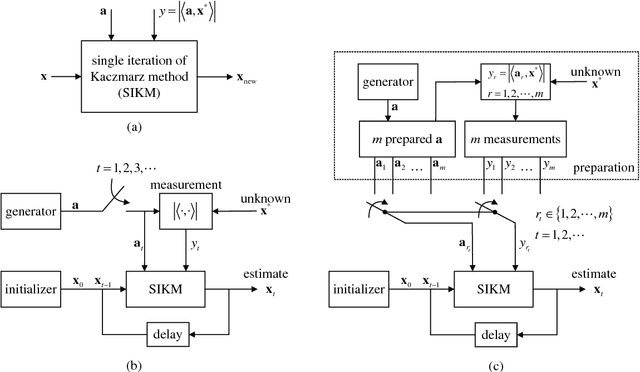
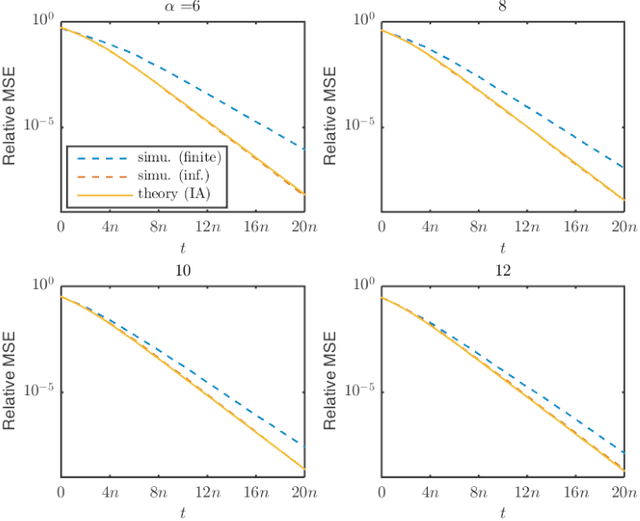
Phase retrieval has been an attractive but difficult problem rising from physical science, and there has been a gap between state-of-the-art theoretical convergence analyses and the corresponding efficient retrieval methods. Firstly, these analyses all assume that the sensing vectors and the iterative updates are independent, which only fits the ideal model with infinite measurements but not the reality, where data are limited and have to be reused. Secondly, the empirical results of some efficient methods, such as the randomized Kaczmarz method, show linear convergence, which is beyond existing theoretical explanations considering its randomness and reuse of data. In this work, we study for the first time, without the independence assumption, the convergence behavior of the randomized Kaczmarz method for phase retrieval. Specifically, beginning from taking expectation of the squared estimation error with respect to the index of measurement by fixing the sensing vector and the error in the previous step, we discard the independence assumption, rigorously derive the upper and lower bounds of the reduction of the mean squared error, and prove the linear convergence. This work fills the gap between a fast converging algorithm and its theoretical understanding. The proposed methodology may contribute to the study of other iterative algorithms for phase retrieval and other problems in the broad area of signal processing and machine learning.