Sobolev Independence Criterion

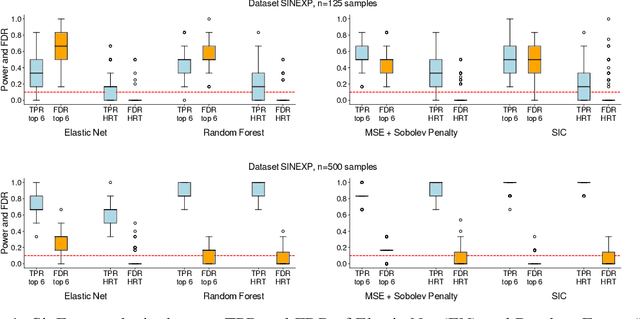
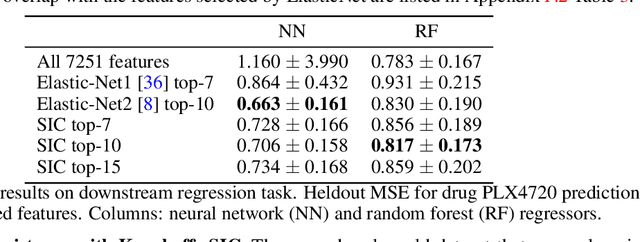
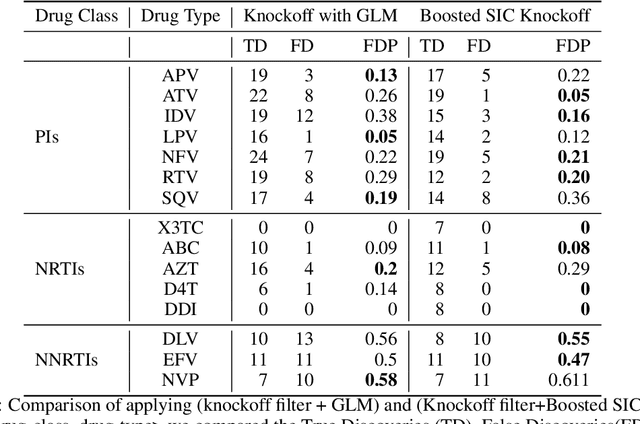
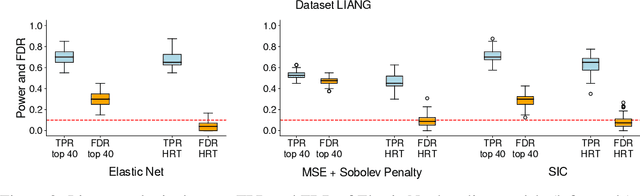
We propose the Sobolev Independence Criterion (SIC), an interpretable dependency measure between a high dimensional random variable X and a response variable Y . SIC decomposes to the sum of feature importance scores and hence can be used for nonlinear feature selection. SIC can be seen as a gradient regularized Integral Probability Metric (IPM) between the joint distribution of the two random variables and the product of their marginals. We use sparsity inducing gradient penalties to promote input sparsity of the critic of the IPM. In the kernel version we show that SIC can be cast as a convex optimization problem by introducing auxiliary variables that play an important role in feature selection as they are normalized feature importance scores. We then present a neural version of SIC where the critic is parameterized as a homogeneous neural network, improving its representation power as well as its interpretability. We conduct experiments validating SIC for feature selection in synthetic and real-world experiments. We show that SIC enables reliable and interpretable discoveries, when used in conjunction with the holdout randomization test and knockoffs to control the False Discovery Rate. Code is available at http://github.com/ibm/sic.

Decentralized Parallel Algorithm for Training Generative Adversarial Nets

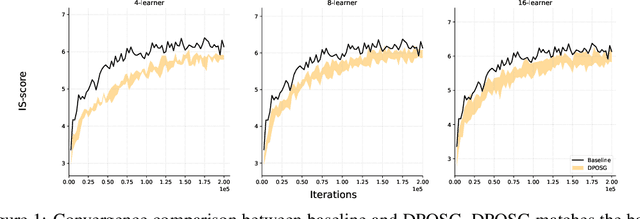
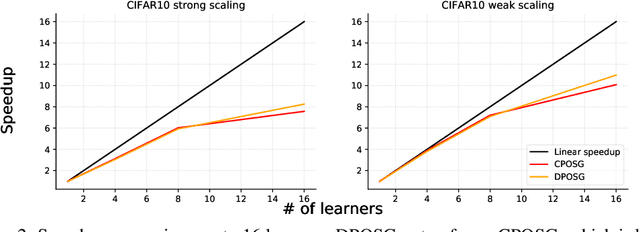
Generative Adversarial Networks (GANs) are powerful class of generative models in the deep learning community. Current practice on large-scale GAN training \cite{brock2018large} utilizes large models and distributed large-batch training strategies, and is implemented on deep learning frameworks (e.g., TensorFlow, PyTorch, etc.) designed in a centralized manner. In the centralized network topology, every worker needs to communicate with the central node. However, when the network bandwidth is low or network latency is high, the performance would be significantly degraded. Despite recent progress on decentralized algorithms for training deep neural networks, it remains unclear whether it is possible to train GANs in a decentralized manner. In this paper, we design a decentralized algorithm for solving a class of non-convex non-concave min-max problem with provable guarantee. Experimental results on GANs demonstrate the effectiveness of the proposed algorithm.

Wasserstein Style Transfer

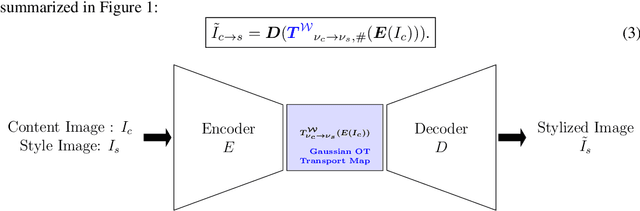
We propose Gaussian optimal transport for Image style transfer in an Encoder/Decoder framework. Optimal transport for Gaussian measures has closed forms Monge mappings from source to target distributions. Moreover interpolates between a content and a style image can be seen as geodesics in the Wasserstein Geometry. Using this insight, we show how to mix different target styles , using Wasserstein barycenter of Gaussian measures. Since Gaussians are closed under Wasserstein barycenter, this allows us a simple style transfer and style mixing and interpolation. Moreover we show how mixing different styles can be achieved using other geodesic metrics between gaussians such as the Fisher Rao metric, while the transport of the content to the new interpolate style is still performed with Gaussian OT maps. Our simple methodology allows to generate new stylized content interpolating between many artistic styles. The metric used in the interpolation results in different stylizations.

Learning Implicit Generative Models by Matching Perceptual Features

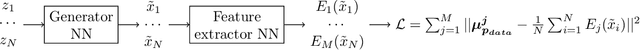
Perceptual features (PFs) have been used with great success in tasks such as transfer learning, style transfer, and super-resolution. However, the efficacy of PFs as key source of information for learning generative models is not well studied. We investigate here the use of PFs in the context of learning implicit generative models through moment matching (MM). More specifically, we propose a new effective MM approach that learns implicit generative models by performing mean and covariance matching of features extracted from pretrained ConvNets. Our proposed approach improves upon existing MM methods by: (1) breaking away from the problematic min/max game of adversarial learning; (2) avoiding online learning of kernel functions; and (3) being efficient with respect to both number of used moments and required minibatch size. Our experimental results demonstrate that, due to the expressiveness of PFs from pretrained deep ConvNets, our method achieves state-of-the-art results for challenging benchmarks.

Implicit Kernel Learning

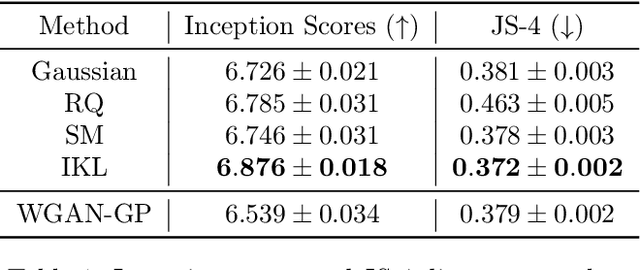
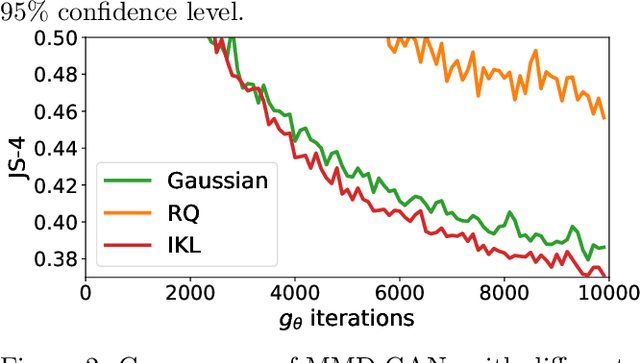
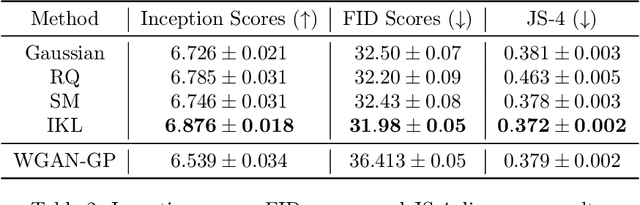
Kernels are powerful and versatile tools in machine learning and statistics. Although the notion of universal kernels and characteristic kernels has been studied, kernel selection still greatly influences the empirical performance. While learning the kernel in a data driven way has been investigated, in this paper we explore learning the spectral distribution of kernel via implicit generative models parametrized by deep neural networks. We called our method Implicit Kernel Learning (IKL). The proposed framework is simple to train and inference is performed via sampling random Fourier features. We investigate two applications of the proposed IKL as examples, including generative adversarial networks with MMD (MMD GAN) and standard supervised learning. Empirically, MMD GAN with IKL outperforms vanilla predefined kernels on both image and text generation benchmarks; using IKL with Random Kitchen Sinks also leads to substantial improvement over existing state-of-the-art kernel learning algorithms on popular supervised learning benchmarks. Theory and conditions for using IKL in both applications are also studied as well as connections to previous state-of-the-art methods.

Wasserstein Barycenter Model Ensembling

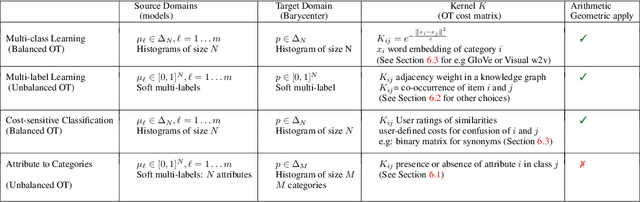
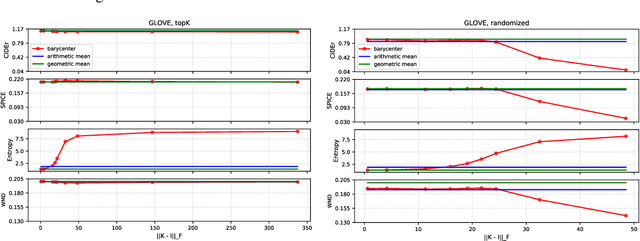
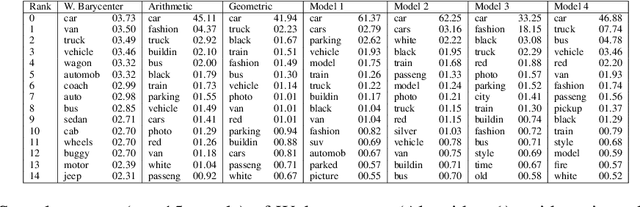
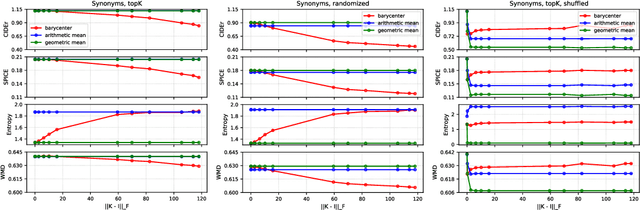
In this paper we propose to perform model ensembling in a multiclass or a multilabel learning setting using Wasserstein (W.) barycenters. Optimal transport metrics, such as the Wasserstein distance, allow incorporating semantic side information such as word embeddings. Using W. barycenters to find the consensus between models allows us to balance confidence and semantics in finding the agreement between the models. We show applications of Wasserstein ensembling in attribute-based classification, multilabel learning and image captioning generation. These results show that the W. ensembling is a viable alternative to the basic geometric or arithmetic mean ensembling.

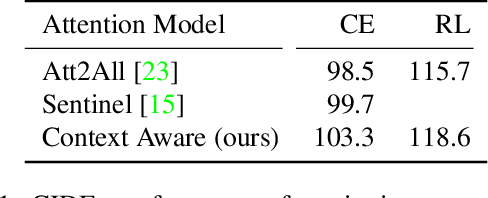
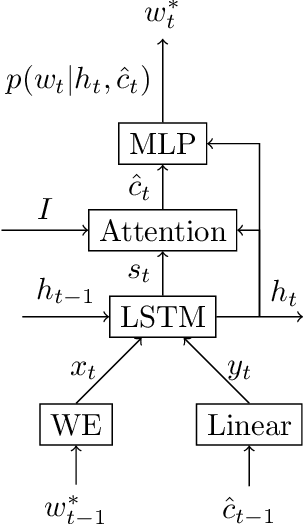
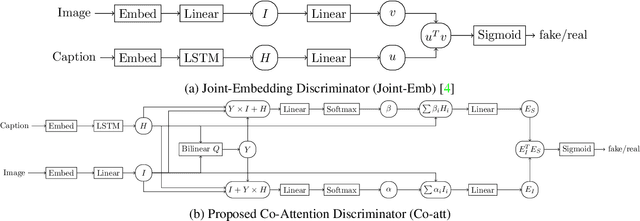
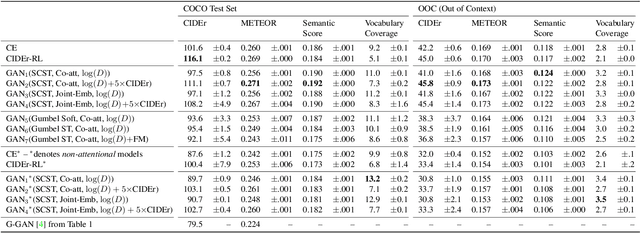
Improved Image Captioning with Adversarial Semantic Alignment

We study image captioning as a conditional GAN training, proposing both a context-aware LSTM captioner and co-attentive discriminator, which enforces semantic alignment between images and captions. We empirically study the viability of two training methods: Self-critical Sequence Training (SCST) and Gumbel Straight-Through (ST). We show that, surprisingly, SCST (a policy gradient method) shows more stable gradient behavior and improved results over Gumbel ST, even without accessing the discriminator gradients directly. We also address the open question of automatic evaluation for these models and introduce a new semantic score and demonstrate its strong correlation to human judgement. As an evaluation paradigm, we suggest that an important criterion is the ability of a captioner to generalize to compositions between objects that do not usually occur together, for which we introduce a captioned Out of Context (OOC) test set. The OOC dataset combined with our semantic score is a new benchmark for the captioning community. Under this OOC benchmark, and the traditional MSCOCO dataset, we show that SCST has a strong performance in both semantic score and human evaluation.

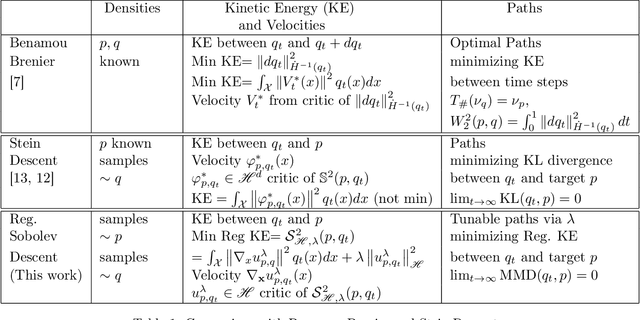
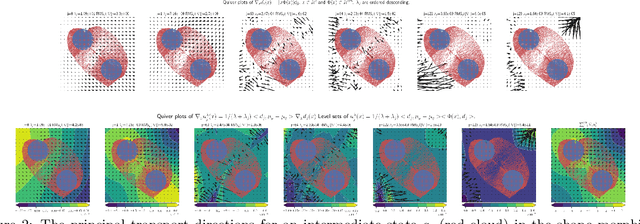
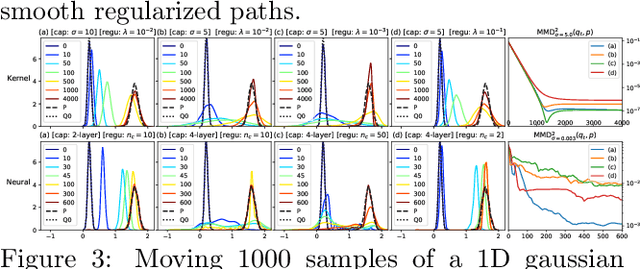
Regularized Kernel and Neural Sobolev Descent: Dynamic MMD Transport

We introduce Regularized Kernel and Neural Sobolev Descent for transporting a source distribution to a target distribution along smooth paths of minimum kinetic energy (defined by the Sobolev discrepancy), related to dynamic optimal transport. In the kernel version, we give a simple algorithm to perform the descent along gradients of the Sobolev critic, and show that it converges asymptotically to the target distribution in the MMD sense. In the neural version, we parametrize the Sobolev critic with a neural network with input gradient norm constrained in expectation. We show in theory and experiments that regularization has an important role in favoring smooth transitions between distributions, avoiding large discrete jumps. Our analysis could provide a new perspective on the impact of critic updates (early stopping) on the paths to equilibrium in the GAN setting.

Regularized Finite Dimensional Kernel Sobolev Discrepancy

We show in this note that the Sobolev Discrepancy introduced in Mroueh et al in the context of generative adversarial networks, is actually the weighted negative Sobolev norm $||.||_{\dot{H}^{-1}(\nu_q)}$, that is known to linearize the Wasserstein $W_2$ distance and plays a fundamental role in the dynamic formulation of optimal transport of Benamou and Brenier. Given a Kernel with finite dimensional feature map we show that the Sobolev discrepancy can be approximated from finite samples. Assuming this discrepancy is finite, the error depends on the approximation error in the function space induced by the finite dimensional feature space kernel and on a statistical error due to the finite sample approximation.

Semi-Supervised Learning with IPM-based GANs: an Empirical Study

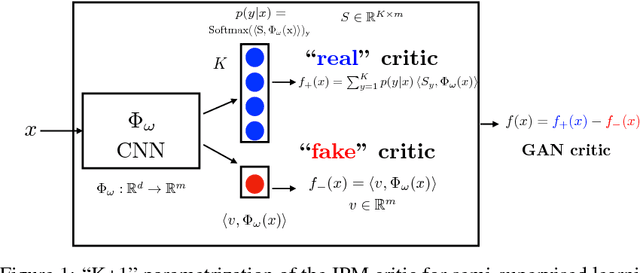
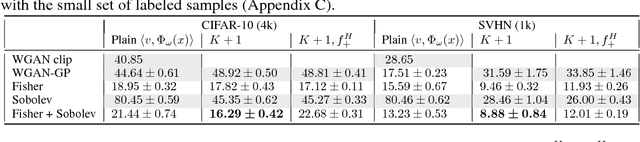
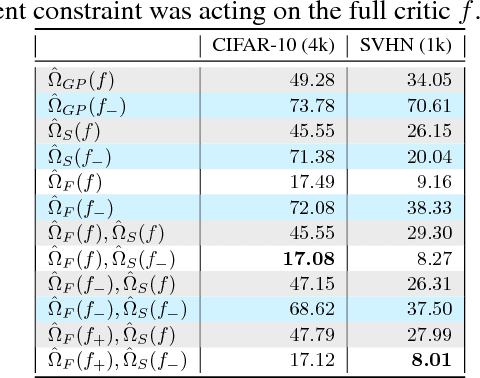
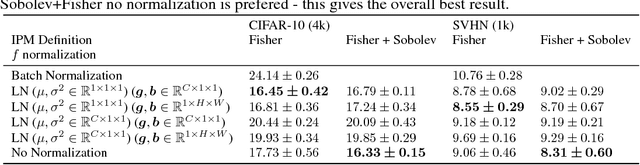
We present an empirical investigation of a recent class of Generative Adversarial Networks (GANs) using Integral Probability Metrics (IPM) and their performance for semi-supervised learning. IPM-based GANs like Wasserstein GAN, Fisher GAN and Sobolev GAN have desirable properties in terms of theoretical understanding, training stability, and a meaningful loss. In this work we investigate how the design of the critic (or discriminator) influences the performance in semi-supervised learning. We distill three key take-aways which are important for good SSL performance: (1) the K+1 formulation, (2) avoiding batch normalization in the critic and (3) avoiding gradient penalty constraints on the classification layer.