Complete Visibility Algorithm for Autonomous Mobile Luminous Robots under an Asynchronous Scheduler on Grid Plane

An autonomous mobile robot system is a distributed system consisting of mobile computational entities (called robots) that autonomously and repeatedly perform three operations: Look, Compute, and Move. Various problems related to autonomous mobile robots, such as gathering, pattern formation, or flocking, have been extensively studied to understand the relationship between each robot's capabilities and the solvability of these problems. In this study, we focus on the complete visibility problem, which involves relocating all the robots on an infinite grid plane such that each robot is visible to every other robot. We assume that each robot is a luminous robot (i.e., has a light with a constant number of colors) and opaque (not transparent). In this paper, we propose an algorithm to achieve complete visibility when a set of robots is given. The algorithm ensures that complete visibility is achieved even when robots operate asynchronously and have no knowledge of the total number of robots on the grid plane using only two colors.

Gathering Despite Defected View

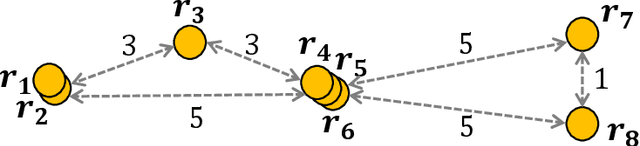
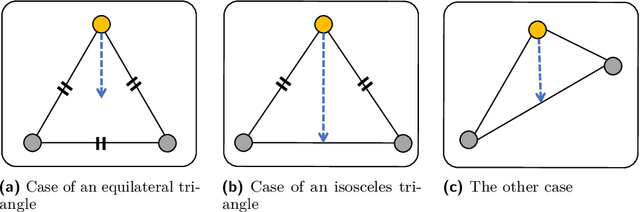
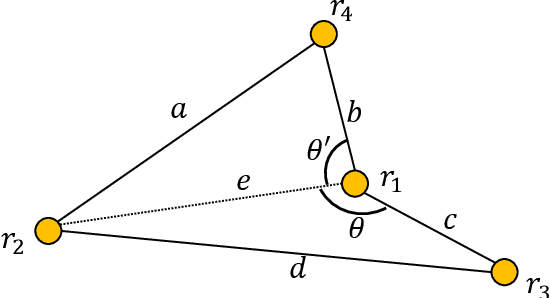
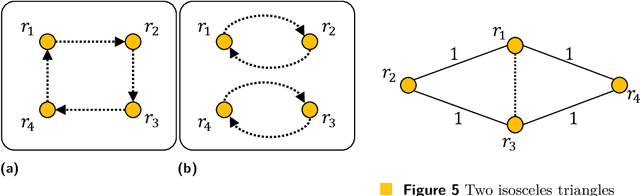
An autonomous mobile robot system consisting of many mobile computational entities (called robots) attracts much attention of researchers, and to clarify the relation between the capabilities of robots and solvability of the problems is an emerging issue for a recent couple of decades. Generally, each robot can observe all other robots as long as there are no restrictions for visibility range or obstructions, regardless of the number of robots. In this paper, we provide a new perspective on the observation by robots; a robot cannot necessarily observe all other robots regardless of distances to them. We call this new computational model defected view model. Under this model, in this paper, we consider the gathering problem that requires all the robots to gather at the same point and propose two algorithms to solve the gathering problem in the adversarial ($N$,$N-2$)-defected model for $N \geq 5$ (where each robot observes at most $N-2$ robots chosen adversarially) and the distance-based (4,2)-defected model (where each robot observes at most 2 closest robots to itself) respectively, where $N$ is the number of robots. Moreover, we present an impossibility result showing that there is no (deterministic) gathering algorithm in the adversarial or distance-based (3,1)-defected model. Moreover, we show an impossibility result for the gathering in a relaxed ($N$, $N-2$)-defected model.

Gathering of seven autonomous mobile robots on triangular grids

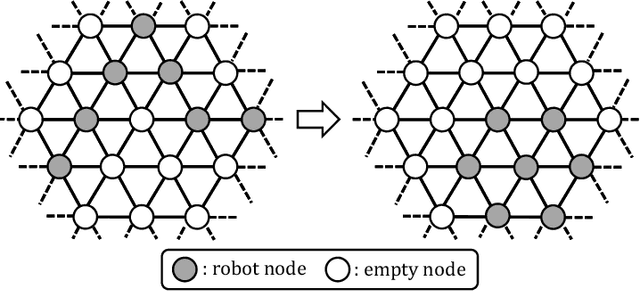
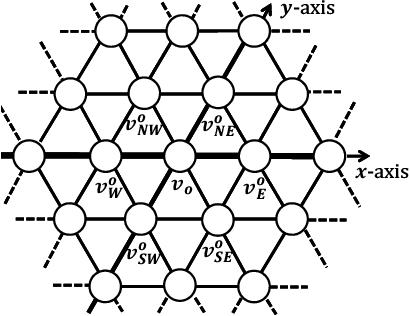
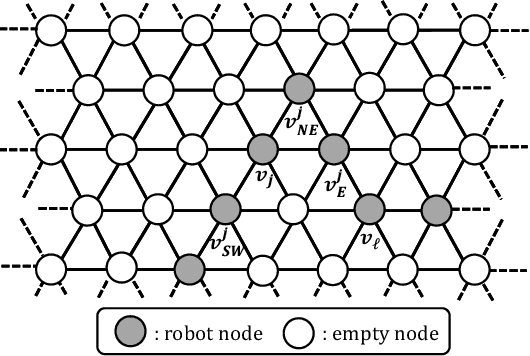
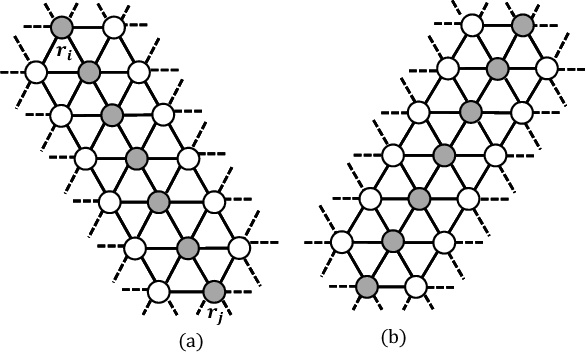
In this paper, we consider the gathering problem of seven autonomous mobile robots on triangular grids. The gathering problem requires that, starting from any connected initial configuration where a subgraph induced by all robot nodes (nodes where a robot exists) constitutes one connected graph, robots reach a configuration such that the maximum distance between two robots is minimized. For the case of seven robots, gathering is achieved when one robot has six adjacent robot nodes (they form a shape like a hexagon). In this paper, we aim to clarify the relationship between the capability of robots and the solvability of gathering on a triangular grid. In particular, we focus on visibility range of robots. To discuss the solvability of the problem in terms of the visibility range, we consider strong assumptions except for visibility range. Concretely, we assume that robots are fully synchronous and they agree on the direction and orientation of the x-axis, and chirality in the triangular grid. In this setting, we first consider the weakest assumption about visibility range, i.e., robots with visibility range 1. In this case, we show that there exists no collision-free algorithm to solve the gathering problem. Next, we extend the visibility range to 2. In this case, we show that our algorithm can solve the problem from any connected initial configuration. Thus, the proposed algorithm is optimal in terms of visibility range.

The Gathering Problem for Two Oblivious Robots with Unreliable Compasses

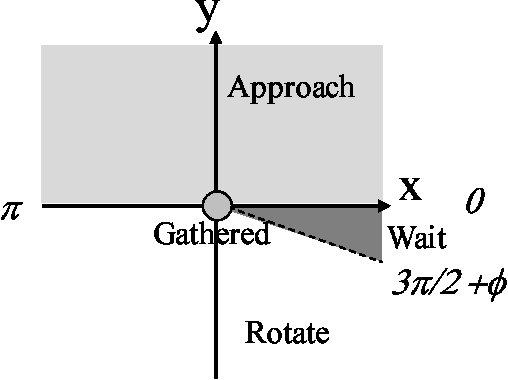
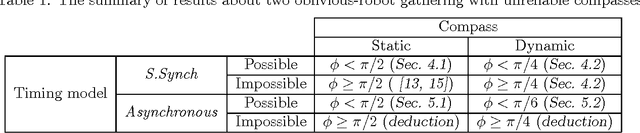
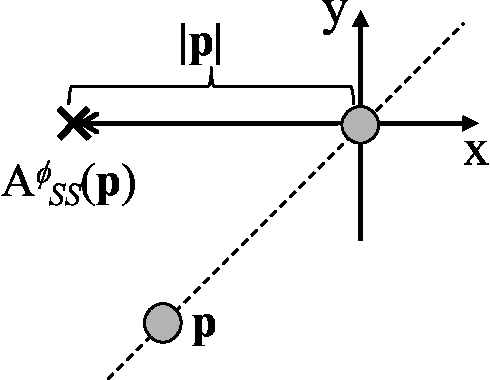
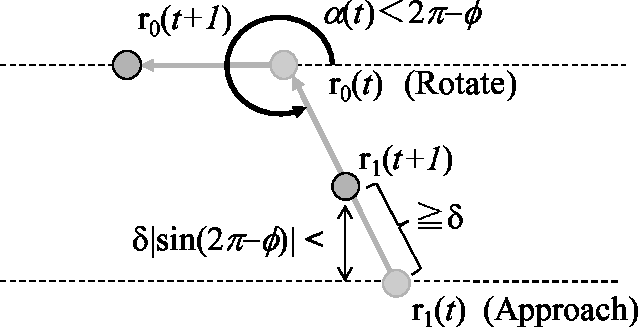
Anonymous mobile robots are often classified into synchronous, semi-synchronous and asynchronous robots when discussing the pattern formation problem. For semi-synchronous robots, all patterns formable with memory are also formable without memory, with the single exception of forming a point (i.e., the gathering) by two robots. However, the gathering problem for two semi-synchronous robots without memory is trivially solvable when their local coordinate systems are consistent, and the impossibility proof essentially uses the inconsistencies in their coordinate systems. Motivated by this, this paper investigates the magnitude of consistency between the local coordinate systems necessary and sufficient to solve the gathering problem for two oblivious robots under semi-synchronous and asynchronous models. To discuss the magnitude of consistency, we assume that each robot is equipped with an unreliable compass, the bearings of which may deviate from an absolute reference direction, and that the local coordinate system of each robot is determined by its compass. We consider two families of unreliable compasses, namely,static compasses with constant bearings, and dynamic compasses the bearings of which can change arbitrarily. For each of the combinations of robot and compass models, we establish the condition on deviation \phi that allows an algorithm to solve the gathering problem, where the deviation is measured by the largest angle formed between the x-axis of a compass and the reference direction of the global coordinate system: \phi < \pi/2 for semi-synchronous and asynchronous robots with static compasses, \phi < \pi/4 for semi-synchronous robots with dynamic compasses, and \phi < \pi/6 for asynchronous robots with dynamic compasses. Except for asynchronous robots with dynamic compasses, these sufficient conditions are also necessary.