Gathering Despite Defected View

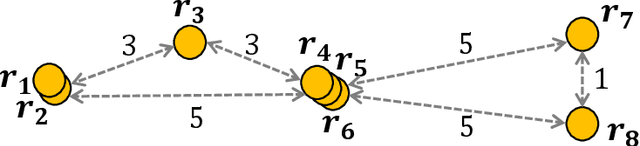
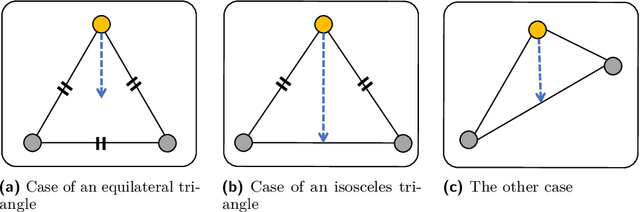
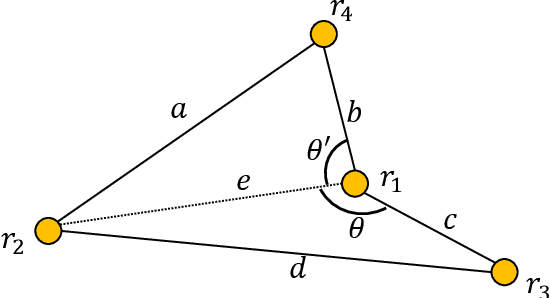
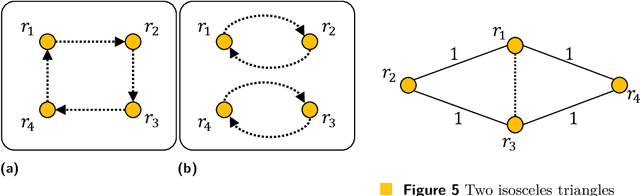
An autonomous mobile robot system consisting of many mobile computational entities (called robots) attracts much attention of researchers, and to clarify the relation between the capabilities of robots and solvability of the problems is an emerging issue for a recent couple of decades. Generally, each robot can observe all other robots as long as there are no restrictions for visibility range or obstructions, regardless of the number of robots. In this paper, we provide a new perspective on the observation by robots; a robot cannot necessarily observe all other robots regardless of distances to them. We call this new computational model defected view model. Under this model, in this paper, we consider the gathering problem that requires all the robots to gather at the same point and propose two algorithms to solve the gathering problem in the adversarial ($N$,$N-2$)-defected model for $N \geq 5$ (where each robot observes at most $N-2$ robots chosen adversarially) and the distance-based (4,2)-defected model (where each robot observes at most 2 closest robots to itself) respectively, where $N$ is the number of robots. Moreover, we present an impossibility result showing that there is no (deterministic) gathering algorithm in the adversarial or distance-based (3,1)-defected model. Moreover, we show an impossibility result for the gathering in a relaxed ($N$, $N-2$)-defected model.

Quiescence of Self-stabilizing Gossiping among Mobile Agents in Graphs

This paper considers gossiping among mobile agents in graphs: agents move on the graph and have to disseminate their initial information to every other agent. We focus on self-stabilizing solutions for the gossip problem, where agents may start from arbitrary locations in arbitrary states. Self-stabilization requires (some of the) participating agents to keep moving forever, hinting at maximizing the number of agents that could be allowed to stop moving eventually. This paper formalizes the self-stabilizing agent gossip problem, introduces the quiescence number (i.e., the maximum number of eventually stopping agents) of self-stabilizing solutions and investigates the quiescence number with respect to several assumptions related to agent anonymity, synchrony, link duplex capacity, and whiteboard capacity.