The Gathering Problem for Two Oblivious Robots with Unreliable Compasses

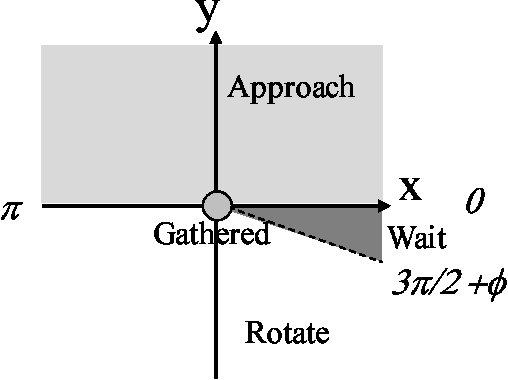
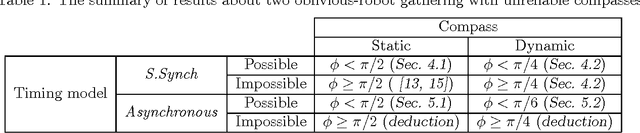
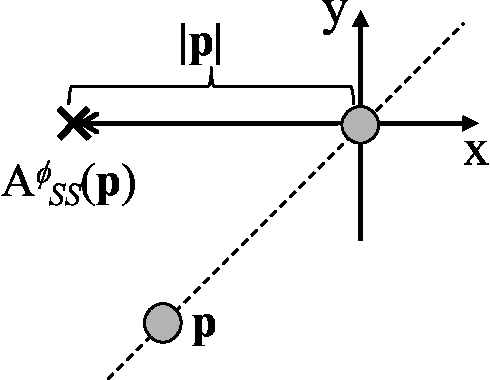
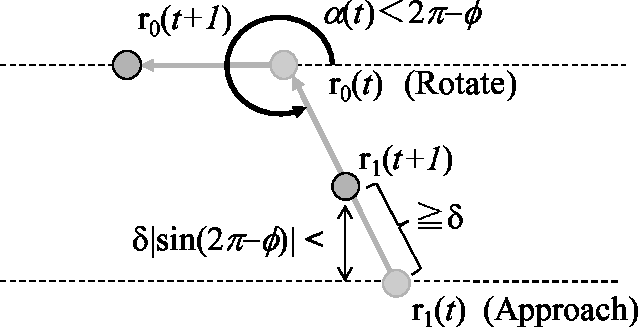
Anonymous mobile robots are often classified into synchronous, semi-synchronous and asynchronous robots when discussing the pattern formation problem. For semi-synchronous robots, all patterns formable with memory are also formable without memory, with the single exception of forming a point (i.e., the gathering) by two robots. However, the gathering problem for two semi-synchronous robots without memory is trivially solvable when their local coordinate systems are consistent, and the impossibility proof essentially uses the inconsistencies in their coordinate systems. Motivated by this, this paper investigates the magnitude of consistency between the local coordinate systems necessary and sufficient to solve the gathering problem for two oblivious robots under semi-synchronous and asynchronous models. To discuss the magnitude of consistency, we assume that each robot is equipped with an unreliable compass, the bearings of which may deviate from an absolute reference direction, and that the local coordinate system of each robot is determined by its compass. We consider two families of unreliable compasses, namely,static compasses with constant bearings, and dynamic compasses the bearings of which can change arbitrarily. For each of the combinations of robot and compass models, we establish the condition on deviation \phi that allows an algorithm to solve the gathering problem, where the deviation is measured by the largest angle formed between the x-axis of a compass and the reference direction of the global coordinate system: \phi < \pi/2 for semi-synchronous and asynchronous robots with static compasses, \phi < \pi/4 for semi-synchronous robots with dynamic compasses, and \phi < \pi/6 for asynchronous robots with dynamic compasses. Except for asynchronous robots with dynamic compasses, these sufficient conditions are also necessary.