Two-Robot Computational Landscape: A Complete Characterization of Model Power in Minimal Mobile Robot Systems

The computational power of autonomous mobile robots under the Look-Compute-Move (LCM) model has been widely studied through an extensive hierarchy of robot models defined by the presence of memory, communication, and synchrony assumptions. While the general n-robot landscape has been largely established, the exact structure for two robots has remained unresolved. This paper presents the first complete characterization of the computational power of two autonomous robots across all major models, namely OBLOT, FSTA, FCOM, and LUMI, under the full spectrum of schedulers (FSYNCH, SSYNCH, ASYNCH, and their atomic variants). Our results reveal a landscape that fundamentally differs from the general case. Most notably, we prove that FSTA^F and LUMI^F coincide under full synchrony, a surprising collapse indicating that perfect synchrony can substitute both memory and communication when only two robots exist. We also show that FSTA and FCOM are orthogonal: there exists a problem solvable in the weakest communication model but impossible even in the strongest finite-state model, completing the bidirectional incomparability. All equivalence and separation results are derived through a novel simulation-free method, providing a unified and constructive view of the two-robot hierarchy. This yields the first complete and exact computational landscape for two robots, highlighting the intrinsic challenges of coordination at the minimal scale.

Gathering Despite Defected View

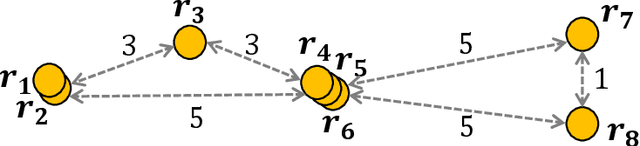
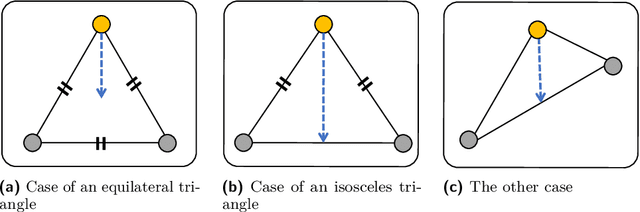
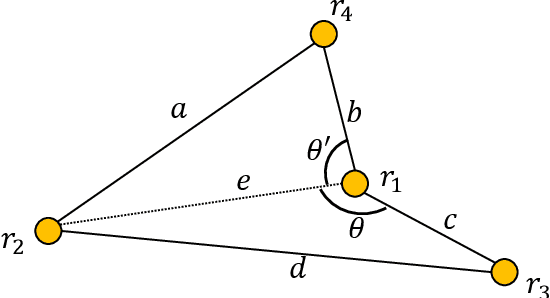
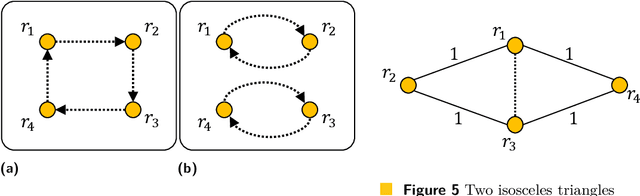
An autonomous mobile robot system consisting of many mobile computational entities (called robots) attracts much attention of researchers, and to clarify the relation between the capabilities of robots and solvability of the problems is an emerging issue for a recent couple of decades. Generally, each robot can observe all other robots as long as there are no restrictions for visibility range or obstructions, regardless of the number of robots. In this paper, we provide a new perspective on the observation by robots; a robot cannot necessarily observe all other robots regardless of distances to them. We call this new computational model defected view model. Under this model, in this paper, we consider the gathering problem that requires all the robots to gather at the same point and propose two algorithms to solve the gathering problem in the adversarial ($N$,$N-2$)-defected model for $N \geq 5$ (where each robot observes at most $N-2$ robots chosen adversarially) and the distance-based (4,2)-defected model (where each robot observes at most 2 closest robots to itself) respectively, where $N$ is the number of robots. Moreover, we present an impossibility result showing that there is no (deterministic) gathering algorithm in the adversarial or distance-based (3,1)-defected model. Moreover, we show an impossibility result for the gathering in a relaxed ($N$, $N-2$)-defected model.

Gathering of seven autonomous mobile robots on triangular grids

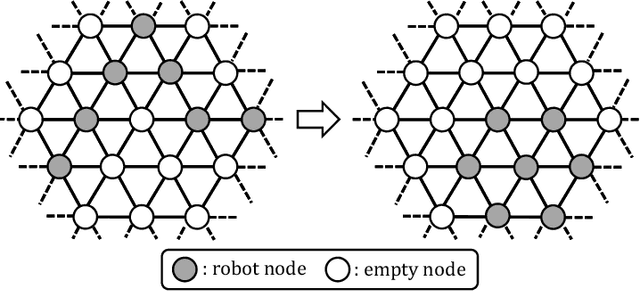
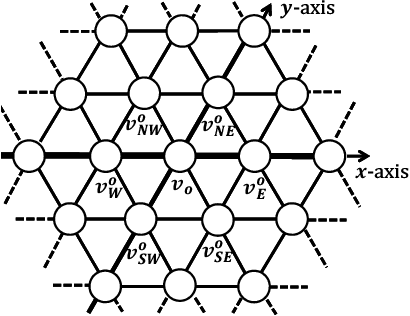
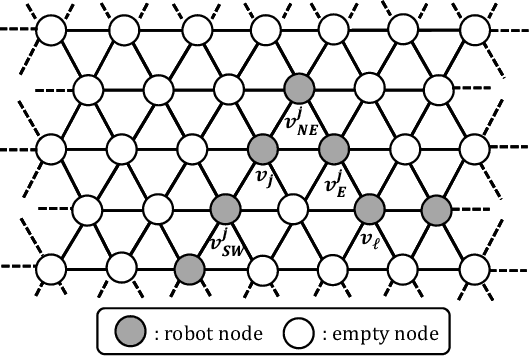
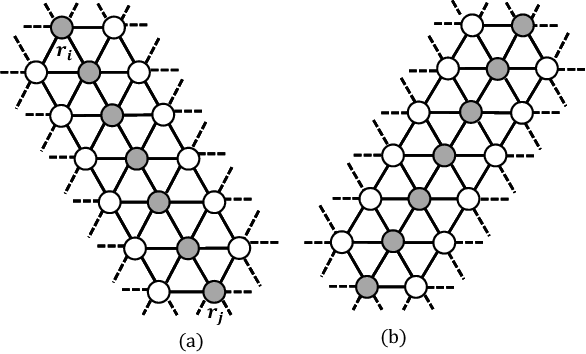
In this paper, we consider the gathering problem of seven autonomous mobile robots on triangular grids. The gathering problem requires that, starting from any connected initial configuration where a subgraph induced by all robot nodes (nodes where a robot exists) constitutes one connected graph, robots reach a configuration such that the maximum distance between two robots is minimized. For the case of seven robots, gathering is achieved when one robot has six adjacent robot nodes (they form a shape like a hexagon). In this paper, we aim to clarify the relationship between the capability of robots and the solvability of gathering on a triangular grid. In particular, we focus on visibility range of robots. To discuss the solvability of the problem in terms of the visibility range, we consider strong assumptions except for visibility range. Concretely, we assume that robots are fully synchronous and they agree on the direction and orientation of the x-axis, and chirality in the triangular grid. In this setting, we first consider the weakest assumption about visibility range, i.e., robots with visibility range 1. In this case, we show that there exists no collision-free algorithm to solve the gathering problem. Next, we extend the visibility range to 2. In this case, we show that our algorithm can solve the problem from any connected initial configuration. Thus, the proposed algorithm is optimal in terms of visibility range.