Two-Robot Computational Landscape: A Complete Characterization of Model Power in Minimal Mobile Robot Systems

The computational power of autonomous mobile robots under the Look-Compute-Move (LCM) model has been widely studied through an extensive hierarchy of robot models defined by the presence of memory, communication, and synchrony assumptions. While the general n-robot landscape has been largely established, the exact structure for two robots has remained unresolved. This paper presents the first complete characterization of the computational power of two autonomous robots across all major models, namely OBLOT, FSTA, FCOM, and LUMI, under the full spectrum of schedulers (FSYNCH, SSYNCH, ASYNCH, and their atomic variants). Our results reveal a landscape that fundamentally differs from the general case. Most notably, we prove that FSTA^F and LUMI^F coincide under full synchrony, a surprising collapse indicating that perfect synchrony can substitute both memory and communication when only two robots exist. We also show that FSTA and FCOM are orthogonal: there exists a problem solvable in the weakest communication model but impossible even in the strongest finite-state model, completing the bidirectional incomparability. All equivalence and separation results are derived through a novel simulation-free method, providing a unified and constructive view of the two-robot hierarchy. This yields the first complete and exact computational landscape for two robots, highlighting the intrinsic challenges of coordination at the minimal scale.

Complete Visibility Algorithm for Autonomous Mobile Luminous Robots under an Asynchronous Scheduler on Grid Plane

An autonomous mobile robot system is a distributed system consisting of mobile computational entities (called robots) that autonomously and repeatedly perform three operations: Look, Compute, and Move. Various problems related to autonomous mobile robots, such as gathering, pattern formation, or flocking, have been extensively studied to understand the relationship between each robot's capabilities and the solvability of these problems. In this study, we focus on the complete visibility problem, which involves relocating all the robots on an infinite grid plane such that each robot is visible to every other robot. We assume that each robot is a luminous robot (i.e., has a light with a constant number of colors) and opaque (not transparent). In this paper, we propose an algorithm to achieve complete visibility when a set of robots is given. The algorithm ensures that complete visibility is achieved even when robots operate asynchronously and have no knowledge of the total number of robots on the grid plane using only two colors.

The Gathering Problem for Two Oblivious Robots with Unreliable Compasses

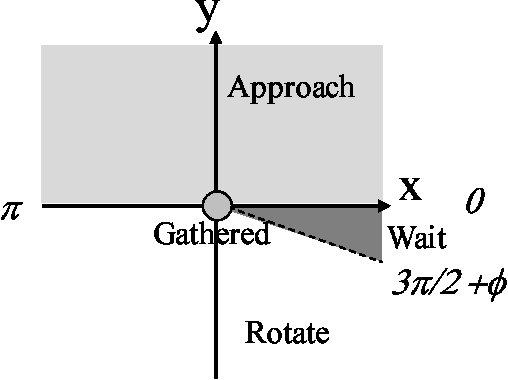
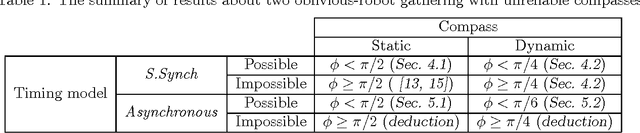
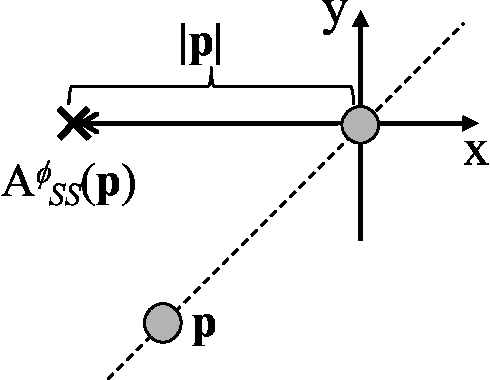
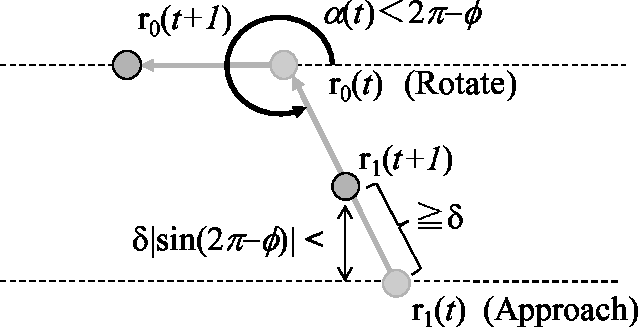
Anonymous mobile robots are often classified into synchronous, semi-synchronous and asynchronous robots when discussing the pattern formation problem. For semi-synchronous robots, all patterns formable with memory are also formable without memory, with the single exception of forming a point (i.e., the gathering) by two robots. However, the gathering problem for two semi-synchronous robots without memory is trivially solvable when their local coordinate systems are consistent, and the impossibility proof essentially uses the inconsistencies in their coordinate systems. Motivated by this, this paper investigates the magnitude of consistency between the local coordinate systems necessary and sufficient to solve the gathering problem for two oblivious robots under semi-synchronous and asynchronous models. To discuss the magnitude of consistency, we assume that each robot is equipped with an unreliable compass, the bearings of which may deviate from an absolute reference direction, and that the local coordinate system of each robot is determined by its compass. We consider two families of unreliable compasses, namely,static compasses with constant bearings, and dynamic compasses the bearings of which can change arbitrarily. For each of the combinations of robot and compass models, we establish the condition on deviation \phi that allows an algorithm to solve the gathering problem, where the deviation is measured by the largest angle formed between the x-axis of a compass and the reference direction of the global coordinate system: \phi < \pi/2 for semi-synchronous and asynchronous robots with static compasses, \phi < \pi/4 for semi-synchronous robots with dynamic compasses, and \phi < \pi/6 for asynchronous robots with dynamic compasses. Except for asynchronous robots with dynamic compasses, these sufficient conditions are also necessary.

The BG-simulation for Byzantine Mobile Robots

This paper investigates the task solvability of mobile robot systems subject to Byzantine faults. We first consider the gathering problem, which requires all robots to meet in finite time at a non-predefined location. It is known that the solvability of Byzantine gathering strongly depends on a number of system attributes, such as synchrony, the number of Byzantine robots, scheduling strategy, obliviousness, orientation of local coordinate systems and so on. However, the complete characterization of the attributes making Byzantine gathering solvable still remains open. In this paper, we show strong impossibility results of Byzantine gathering. Namely, we prove that Byzantine gathering is impossible even if we assume one Byzantine fault, an atomic execution system, the n-bounded centralized scheduler, non-oblivious robots, instantaneous movements and a common orientation of local coordinate systems (where n denote the number of correct robots). Those hypotheses are much weaker than used in previous work, inducing a much stronger impossibility result. At the core of our impossibility result is a reduction from the distributed consensus problem in asynchronous shared-memory systems. In more details, we newly construct a generic reduction scheme based on the distributed BG-simulation. Interestingly, because of its versatility, we can easily extend our impossibility result for general pattern formation problems.