Multiphysics Bench: Benchmarking and Investigating Scientific Machine Learning for Multiphysics PDEs

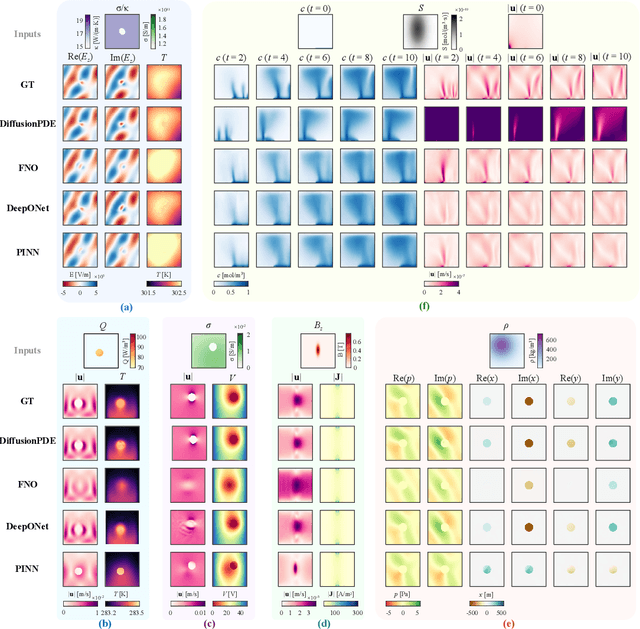
Solving partial differential equations (PDEs) with machine learning has recently attracted great attention, as PDEs are fundamental tools for modeling real-world systems that range from fundamental physical science to advanced engineering disciplines. Most real-world physical systems across various disciplines are actually involved in multiple coupled physical fields rather than a single field. However, previous machine learning studies mainly focused on solving single-field problems, but overlooked the importance and characteristics of multiphysics problems in real world. Multiphysics PDEs typically entail multiple strongly coupled variables, thereby introducing additional complexity and challenges, such as inter-field coupling. Both benchmarking and solving multiphysics problems with machine learning remain largely unexamined. To identify and address the emerging challenges in multiphysics problems, we mainly made three contributions in this work. First, we collect the first general multiphysics dataset, the Multiphysics Bench, that focuses on multiphysics PDE solving with machine learning. Multiphysics Bench is also the most comprehensive PDE dataset to date, featuring the broadest range of coupling types, the greatest diversity of PDE formulations, and the largest dataset scale. Second, we conduct the first systematic investigation on multiple representative learning-based PDE solvers, such as PINNs, FNO, DeepONet, and DiffusionPDE solvers, on multiphysics problems. Unfortunately, naively applying these existing solvers usually show very poor performance for solving multiphysics. Third, through extensive experiments and discussions, we report multiple insights and a bag of useful tricks for solving multiphysics with machine learning, motivating future directions in the study and simulation of complex, coupled physical systems.

High Noise Immune Time-domain Inversion via Cascade Network for Complex Scatterers

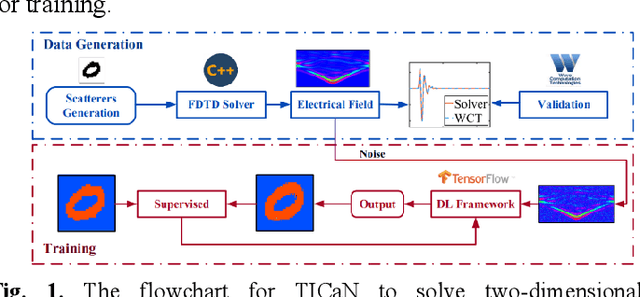
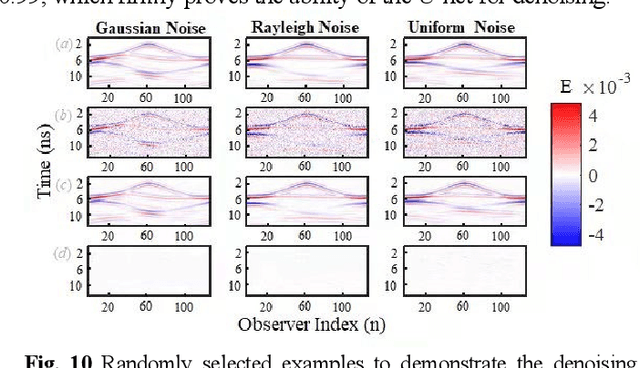
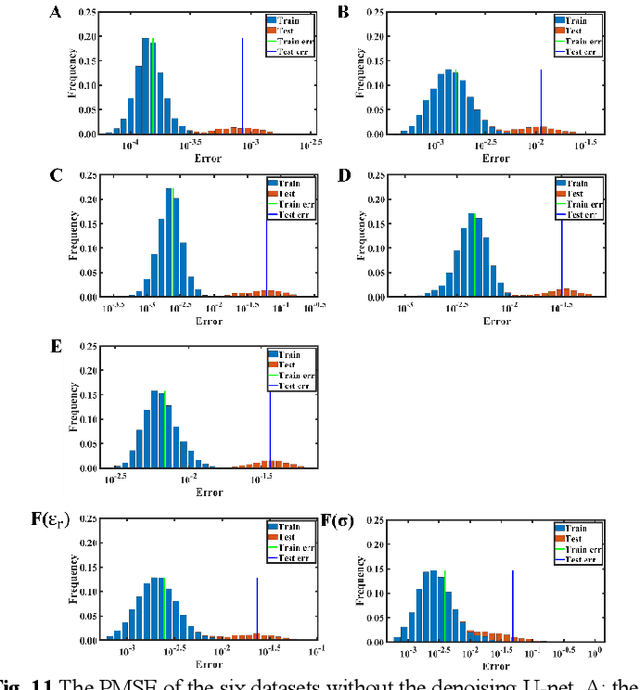
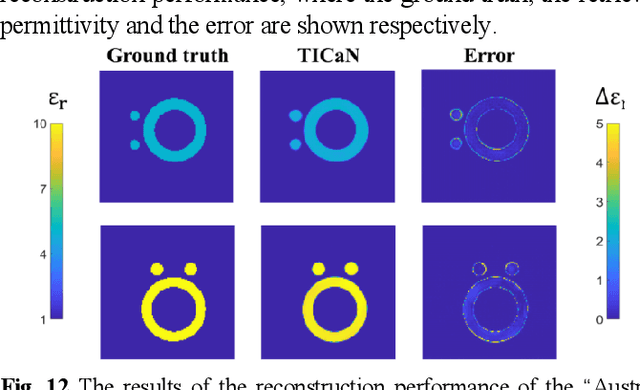
In this paper, a high noise immune time-domain inversion cascade network (TICaN) is proposed to reconstruct scatterers from the measured electromagnetic fields. The TICaN is comprised of a denoising block aiming at improving the signal-to-noise ratio, and an inversion block to reconstruct the electromagnetic properties from the raw time-domain measurements. The scatterers investigated in this study include complicated geometry shapes and high contrast, which cover the stratum layer, lossy medium and hyperfine structure, etc. After being well trained, the performance of the TICaN is evaluated from the perspective of accuracy, noise-immunity, computational acceleration, and generalizability. It can be proven that the proposed framework can realize high-precision inversion under high-intensity noise environments. Compared with traditional reconstruction methods, TICaN avoids the tedious iterative calculation by utilizing the parallel computing ability of GPU and thus significantly reduce the computing time. Besides, the proposed TICaN has certain generalization ability in reconstructing the unknown scatterers such as the famous Austria rings. Herein, it is confident that the proposed TICaN will serve as a new path for real-time quantitative microwave imaging for various practical scenarios.