Find Your Friends: Personalized Federated Learning with the Right Collaborators

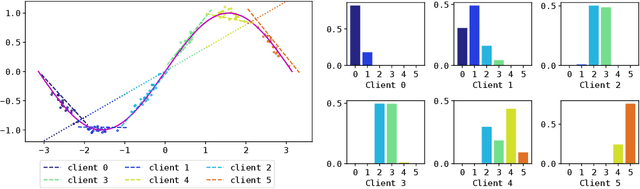
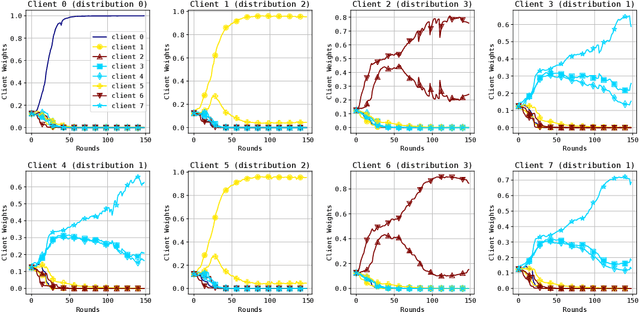
In the traditional federated learning setting, a central server coordinates a network of clients to train one global model. However, the global model may serve many clients poorly due to data heterogeneity. Moreover, there may not exist a trusted central party that can coordinate the clients to ensure that each of them can benefit from others. To address these concerns, we present a novel decentralized framework, FedeRiCo, where each client can learn as much or as little from other clients as is optimal for its local data distribution. Based on expectation-maximization, FedeRiCo estimates the utilities of other participants' models on each client's data so that everyone can select the right collaborators for learning. As a result, our algorithm outperforms other federated, personalized, and/or decentralized approaches on several benchmark datasets, being the only approach that consistently performs better than training with local data only.

Short-and-Sparse Deconvolution -- A Geometric Approach

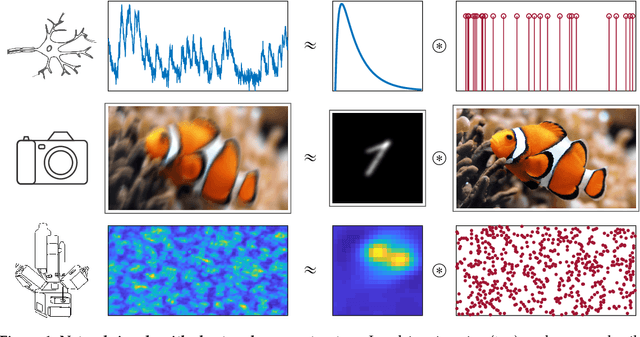
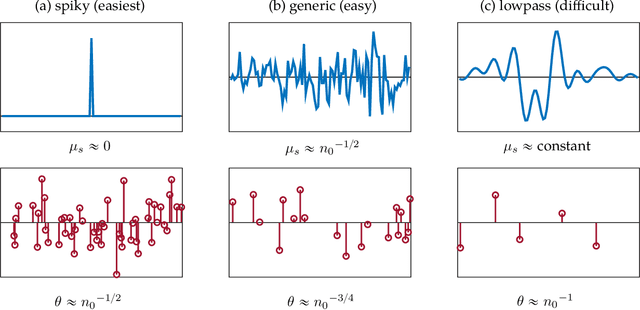
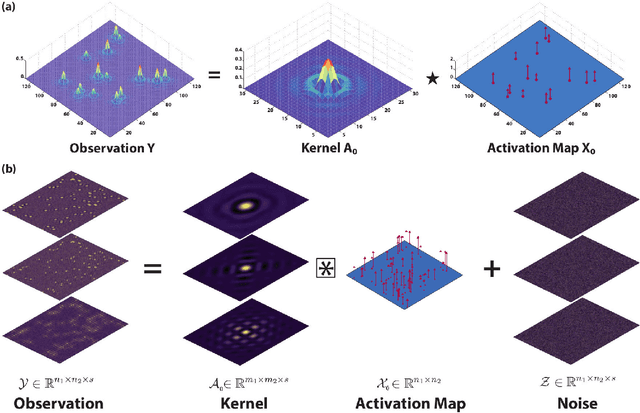
Short-and-sparse deconvolution (SaSD) is the problem of extracting localized, recurring motifs in signals with spatial or temporal structure. Variants of this problem arise in applications such as image deblurring, microscopy, neural spike sorting, and more. The problem is challenging in both theory and practice, as natural optimization formulations are nonconvex. Moreover, practical deconvolution problems involve smooth motifs (kernels) whose spectra decay rapidly, resulting in poor conditioning and numerical challenges. This paper is motivated by recent theoretical advances, which characterize the optimization landscape of a particular nonconvex formulation of SaSD. This is used to derive a $provable$ algorithm which exactly solves certain non-practical instances of the SaSD problem. We leverage the key ideas from this theory (sphere constraints, data-driven initialization) to develop a $practical$ algorithm, which performs well on data arising from a range of application areas. We highlight key additional challenges posed by the ill-conditioning of real SaSD problems, and suggest heuristics (acceleration, continuation, reweighting) to mitigate them. Experiments demonstrate both the performance and generality of the proposed method.

On the Global Geometry of Sphere-Constrained Sparse Blind Deconvolution

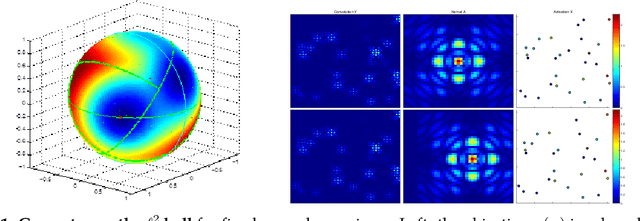
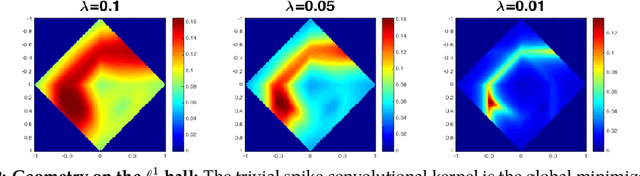
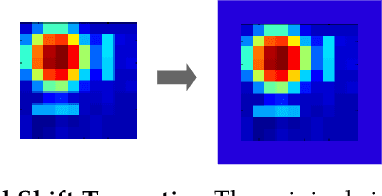
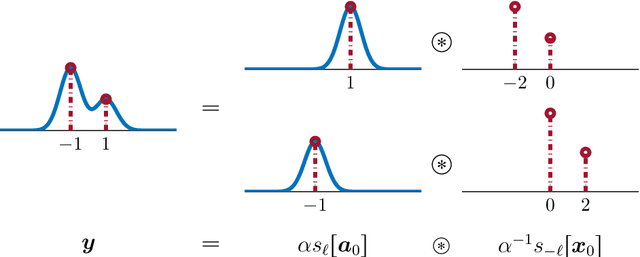
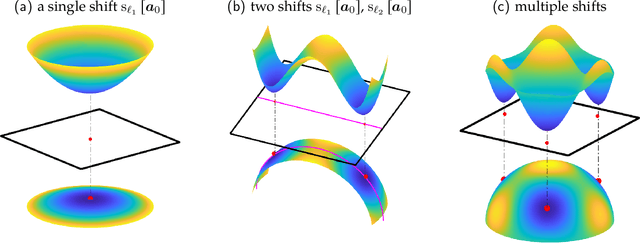
Blind deconvolution is the problem of recovering a convolutional kernel $\boldsymbol a_0$ and an activation signal $\boldsymbol x_0$ from their convolution $\boldsymbol y = \boldsymbol a_0 \circledast \boldsymbol x_0$. This problem is ill-posed without further constraints or priors. This paper studies the situation where the nonzero entries in the activation signal are sparsely and randomly populated. We normalize the convolution kernel to have unit Frobenius norm and cast the sparse blind deconvolution problem as a nonconvex optimization problem over the sphere. With this spherical constraint, every spurious local minimum turns out to be close to some signed shift truncation of the ground truth, under certain hypotheses. This benign property motivates an effective two stage algorithm that recovers the ground truth from the partial information offered by a suboptimal local minimum. This geometry-inspired algorithm recovers the ground truth for certain microscopy problems, also exhibits promising performance in the more challenging image deblurring problem. Our insights into the global geometry and the two stage algorithm extend to the convolutional dictionary learning problem, where a superposition of multiple convolution signals is observed.

Geometry and Symmetry in Short-and-Sparse Deconvolution

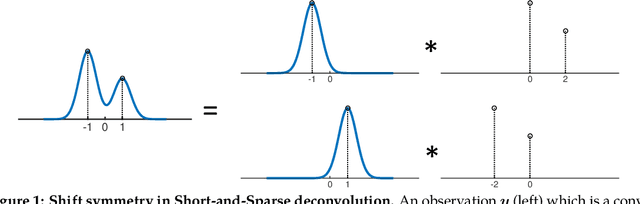
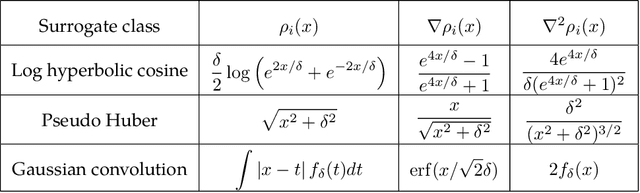
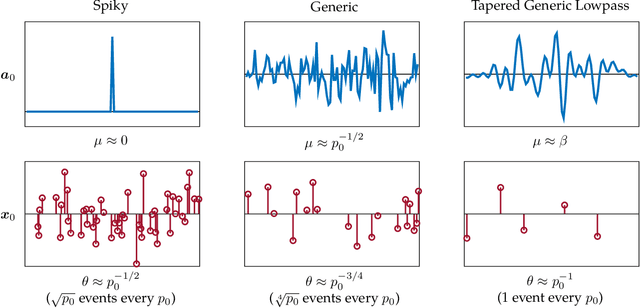
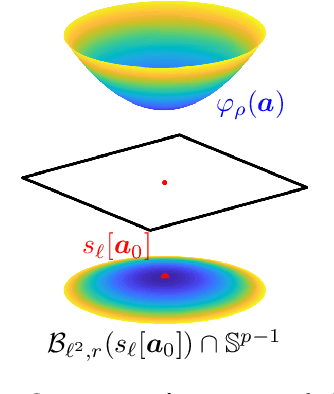
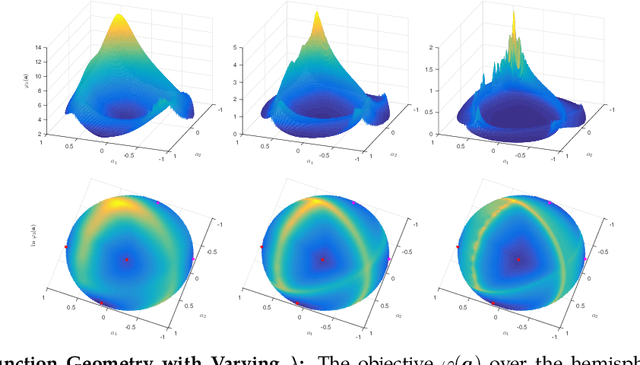
We study the $\textit{Short-and-Sparse (SaS) deconvolution}$ problem of recovering a short signal $\mathbf a_0$ and a sparse signal $\mathbf x_0$ from their convolution. We propose a method based on nonconvex optimization, which under certain conditions recovers the target short and sparse signals, up to a signed shift symmetry which is intrinsic to this model. This symmetry plays a central role in shaping the optimization landscape for deconvolution. We give a $\textit{regional analysis}$, which characterizes this landscape geometrically, on a union of subspaces. Our geometric characterization holds when the length-$p_0$ short signal $\mathbf a_0$ has shift coherence $\mu$, and $\mathbf x_0$ follows a random sparsity model with sparsity rate $\theta \in \Bigl[\frac{c_1}{p_0}, \frac{c_2}{p_0\sqrt\mu + \sqrt{p_0}}\Bigr]\cdot\frac{1}{\log^2p_0}$. Based on this geometry, we give a provable method that successfully solves SaS deconvolution with high probability.

Dictionary Learning in Fourier Transform Scanning Tunneling Spectroscopy

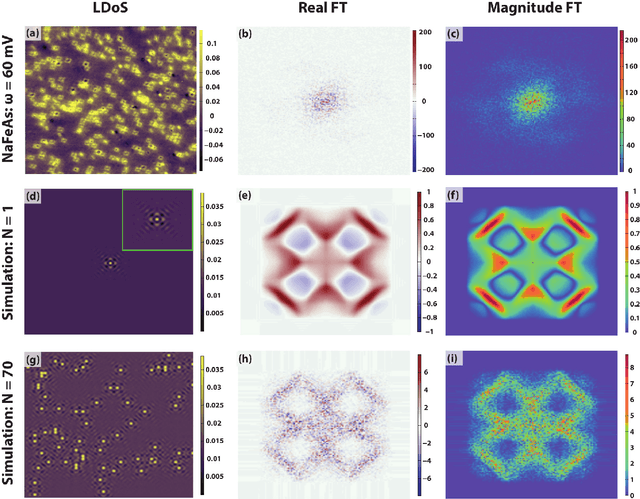
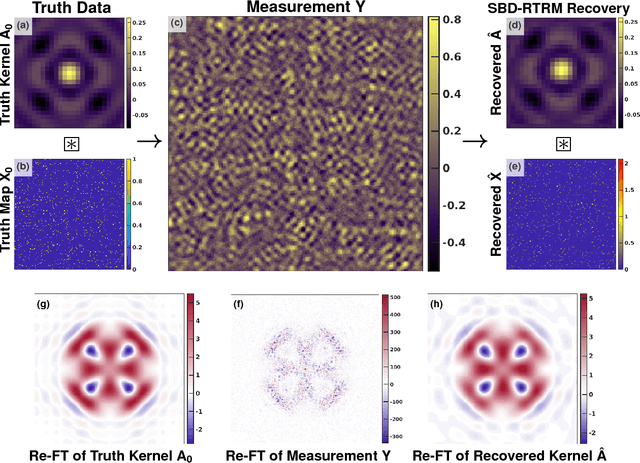
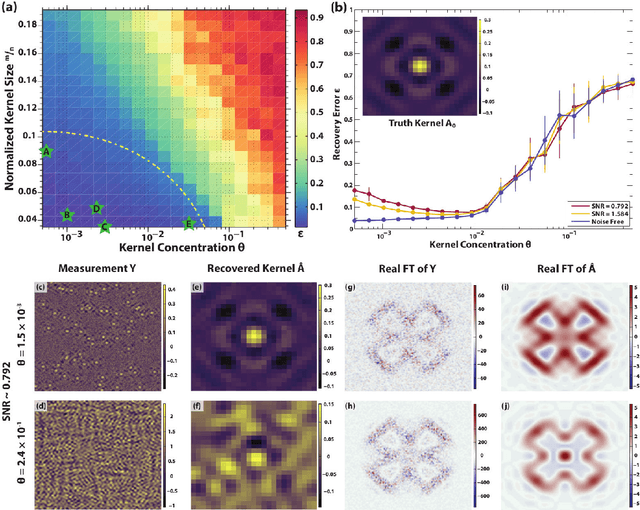
Modern high-resolution microscopes, such as the scanning tunneling microscope, are commonly used to study specimens that have dense and aperiodic spatial structure. Extracting meaningful information from images obtained from such microscopes remains a formidable challenge. Fourier analysis is commonly used to analyze the underlying structure of fundamental motifs present in an image. However, the Fourier transform fundamentally suffers from severe phase noise when applied to aperiodic images. Here, we report the development of a new algorithm based on nonconvex optimization, applicable to any microscopy modality, that directly uncovers the fundamental motifs present in a real-space image. Apart from being quantitatively superior to traditional Fourier analysis, we show that this novel algorithm also uncovers phase sensitive information about the underlying motif structure. We demonstrate its usefulness by studying scanning tunneling microscopy images of a Co-doped iron arsenide superconductor and prove that the application of the algorithm allows for the complete recovery of quasiparticle interference in this material. Our phase sensitive quasiparticle interference imaging results indicate that the pairing symmetry in optimally doped NaFeAs is consistent with a sign-changing s+- order parameter.