Q-Learning with Clustered-SMART (cSMART) Data: Examining Moderators in the Construction of Clustered Adaptive Interventions

A clustered adaptive intervention (cAI) is a pre-specified sequence of decision rules that guides practitioners on how best - and based on which measures - to tailor cluster-level intervention to improve outcomes at the level of individuals within the clusters. A clustered sequential multiple assignment randomized trial (cSMART) is a type of trial that is used to inform the empirical development of a cAI. The most common type of secondary aim in a cSMART focuses on assessing causal effect moderation by candidate tailoring variables. We introduce a clustered Q-learning framework with the M-out-of-N Cluster Bootstrap using data from a cSMART to evaluate whether a set of candidate tailoring variables may be useful in defining an optimal cAI. This approach could construct confidence intervals (CI) with near-nominal coverage to assess parameters indexing the causal effect moderation function. Specifically, it allows reliable inferences concerning the utility of candidate tailoring variables in constructing a cAI that maximizes a mean end-of-study outcome even when "non-regularity", a well-known challenge exists. Simulations demonstrate the numerical performance of the proposed method across varying non-regularity conditions and investigate the impact of varying number of clusters and intra-cluster correlation coefficient on CI coverage. Methods are applied on ADEPT dataset to inform the construction of a clinic-level cAI for improving evidence-based practice in treating mood disorders.

Data-Efficient Characterization of the Global Dynamics of Robot Controllers with Confidence Guarantees

This paper proposes an integration of surrogate modeling and topology to significantly reduce the amount of data required to describe the underlying global dynamics of robot controllers, including closed-box ones. A Gaussian Process (GP), trained with randomized short trajectories over the state-space, acts as a surrogate model for the underlying dynamical system. Then, a combinatorial representation is built and used to describe the dynamics in the form of a directed acyclic graph, known as {\it Morse graph}. The Morse graph is able to describe the system's attractors and their corresponding regions of attraction (\roa). Furthermore, a pointwise confidence level of the global dynamics estimation over the entire state space is provided. In contrast to alternatives, the framework does not require estimation of Lyapunov functions, alleviating the need for high prediction accuracy of the GP. The framework is suitable for data-driven controllers that do not expose an analytical model as long as Lipschitz-continuity is satisfied. The method is compared against established analytical and recent machine learning alternatives for estimating \roa s, outperforming them in data efficiency without sacrificing accuracy. Link to code: https://go.rutgers.edu/49hy35en

CLAIMED: A CLAssification-Incorporated Minimum Energy Design to explore a multivariate response surface with feasibility constraints

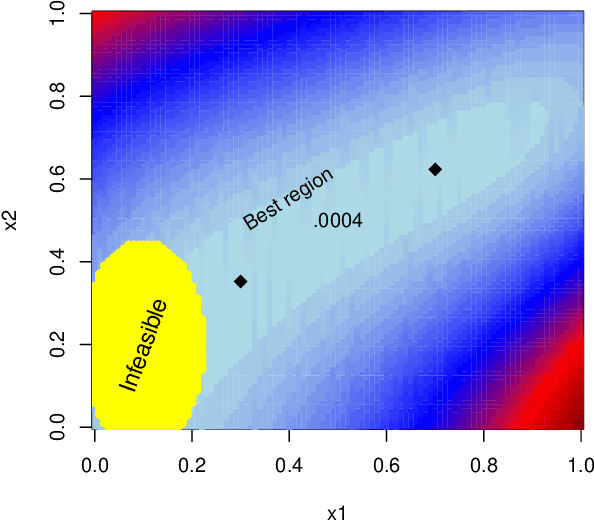
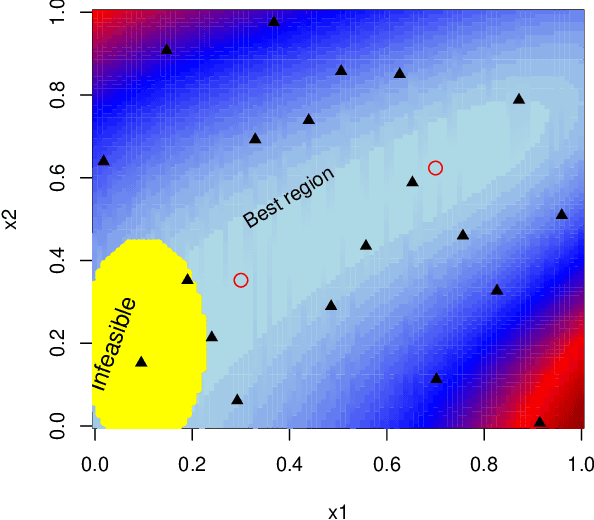
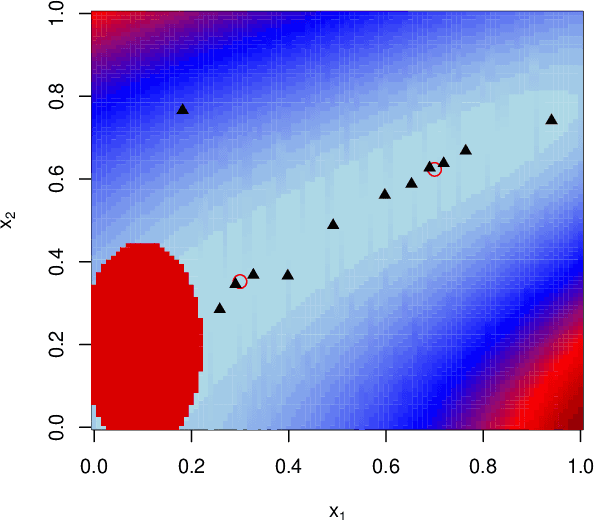
Motivated by the problem of optimization of force-field systems in physics using large-scale computer simulations, we consider exploration of a deterministic complex multivariate response surface. The objective is to find input combinations that generate output close to some desired or "target" vector. In spite of reducing the problem to exploration of the input space with respect to a one-dimensional loss function, the search is nontrivial and challenging due to infeasible input combinations, high dimensionalities of the input and output space and multiple "desirable" regions in the input space and the difficulty of emulating the objective function well with a surrogate model. We propose an approach that is based on combining machine learning techniques with smart experimental design ideas to locate multiple good regions in the input space.