Localization in 1D non-parametric latent space models from pairwise affinities

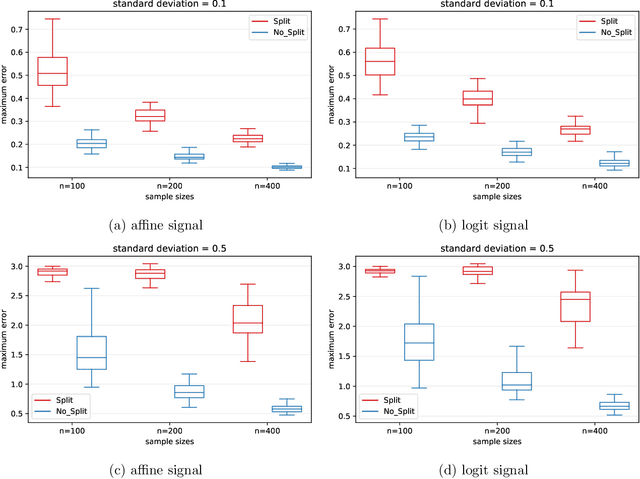
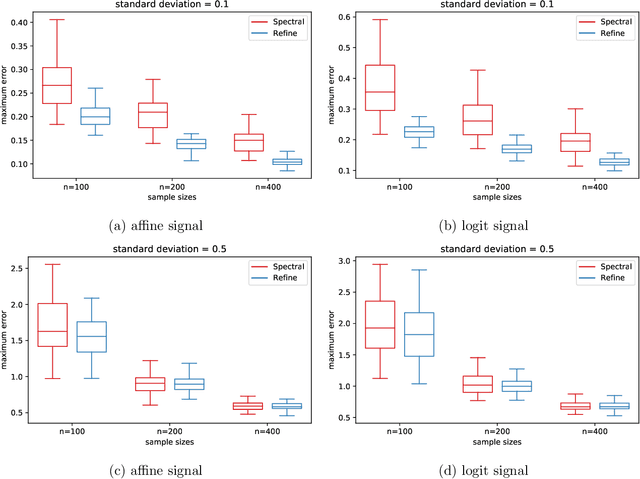
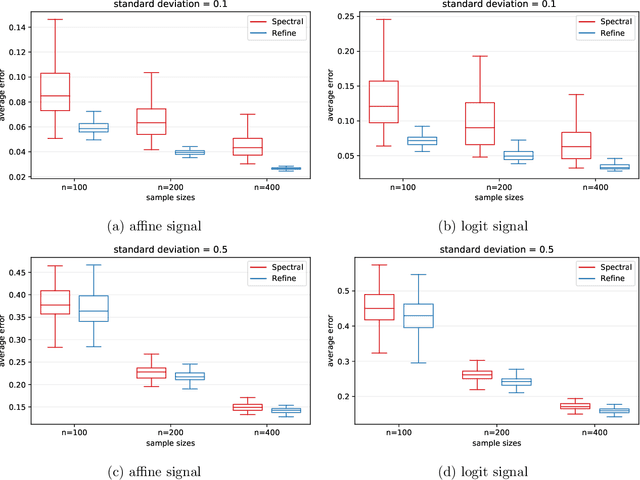
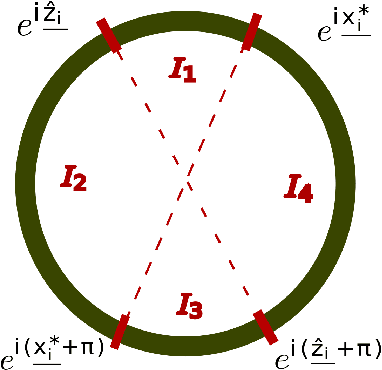
We consider the problem of estimating latent positions in a one-dimensional torus from pairwise affinities. The observed affinity between a pair of items is modeled as a noisy observation of a function $f(x^*_{i},x^*_{j})$ of the latent positions $x^*_{i},x^*_{j}$ of the two items on the torus. The affinity function $f$ is unknown, and it is only assumed to fulfill some shape constraints ensuring that $f(x,y)$ is large when the distance between $x$ and $y$ is small, and vice-versa. This non-parametric modeling offers a good flexibility to fit data. We introduce an estimation procedure that provably localizes all the latent positions with a maximum error of the order of $\sqrt{\log(n)/n}$, with high-probability. This rate is proven to be minimax optimal. A computationally efficient variant of the procedure is also analyzed under some more restrictive assumptions. Our general results can be instantiated to the problem of statistical seriation, leading to new bounds for the maximum error in the ordering.

Locally differentially private estimation of nonlinear functionals of discrete distributions

We study the problem of estimating non-linear functionals of discrete distributions in the context of local differential privacy. The initial data $x_1,\ldots,x_n \in [K]$ are supposed i.i.d. and distributed according to an unknown discrete distribution $p = (p_1,\ldots,p_K)$. Only $\alpha$-locally differentially private (LDP) samples $z_1,...,z_n$ are publicly available, where the term 'local' means that each $z_i$ is produced using one individual attribute $x_i$. We exhibit privacy mechanisms (PM) that are interactive (i.e. they are allowed to use already published confidential data) or non-interactive. We describe the behavior of the quadratic risk for estimating the power sum functional $F_{\gamma} = \sum_{k=1}^K p_k^{\gamma}$, $\gamma >0$ as a function of $K, \, n$ and $\alpha$. In the non-interactive case, we study two plug-in type estimators of $F_{\gamma}$, for all $\gamma >0$, that are similar to the MLE analyzed by Jiao et al. (2017) in the multinomial model. However, due to the privacy constraint the rates we attain are slower and similar to those obtained in the Gaussian model by Collier et al. (2020). In the interactive case, we introduce for all $\gamma >1$ a two-step procedure which attains the faster parametric rate $(n \alpha^2)^{-1/2}$ when $\gamma \geq 2$. We give lower bounds results over all $\alpha$-LDP mechanisms and all estimators using the private samples.

On the Estimation of Network Complexity: Dimension of Graphons

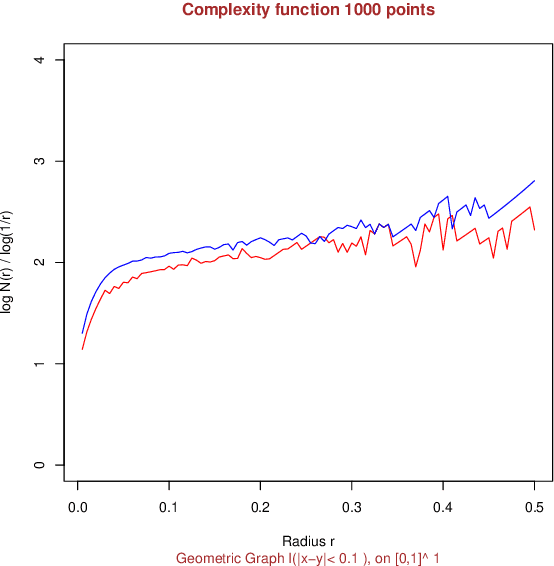
Network complexity has been studied for over half a century and has found a wide range of applications. Many methods have been developed to characterize and estimate the complexity of networks. However, there has been little research with statistical guarantees. In this paper, we develop a statistical theory of graph complexity in a general model of random graphs, the so-called graphon model. Given a graphon, we endow the latent space of the nodes with the so-called neighborhood distance that measures the propensity of two nodes to be connected with similar nodes. Our complexity index is then based on the covering number and the Minkowski dimension of (a purified version of) this metric space. Although the latent space is not identifiable, these indices turn out to be identifiable. This notion of complexity has simple interpretations on popular examples of random graphs: it matches the number of communities in stochastic block models; the dimension of the Euclidean space in random geometric graphs; the regularity of the link function in H\"older graphon models. From a single observation of the graph, we construct an estimator of the neighborhood-distance and show universal non-asymptotic bounds for its risk, matching minimax lower bounds. Based on this estimated distance, we compute the corresponding covering number and Minkowski dimension and we provide optimal non-asymptotic error bounds for these two plug-in estimators.

Pair Matching: When bandits meet stochastic block model

The pair-matching problem appears in many applications where one wants to discover good matches between pairs of individuals. Formally, the set of individuals is represented by the nodes of a graph where the edges, unobserved at first, represent the good matches. The algorithm queries pairs of nodes and observes the presence/absence of edges. Its goal is to discover as many edges as possible with a fixed budget of queries. Pair-matching is a particular instance of multi-armed bandit problem in which the arms are pairs of individuals and the rewards are edges linking these pairs. This bandit problem is non-standard though, as each arm can only be played once. Given this last constraint, sublinear regret can be expected only if the graph presents some underlying structure. This paper shows that sublinear regret is achievable in the case where the graph is generated according to a Stochastic Block Model (SBM) with two communities. Optimal regret bounds are computed for this pair-matching problem. They exhibit a phase transition related to the Kesten-Stigund threshold for community detection in SBM. To avoid undesirable features of optimal solutions, the pair-matching problem is also considered in the case where each node is constrained to be sampled less than a given amount of times. We show how this constraint deteriorates optimal regret rates. The paper is concluded by a conjecture regarding the optimal regret when the number of communities is larger than $2$. Contrary to the two communities case, we believe that a statistical-computational gap would appear in this problem.