Finite-sample performance of the maximum likelihood estimator in logistic regression

Logistic regression is a classical model for describing the probabilistic dependence of binary responses to multivariate covariates. We consider the predictive performance of the maximum likelihood estimator (MLE) for logistic regression, assessed in terms of logistic risk. We consider two questions: first, that of the existence of the MLE (which occurs when the dataset is not linearly separated), and second that of its accuracy when it exists. These properties depend on both the dimension of covariates and on the signal strength. In the case of Gaussian covariates and a well-specified logistic model, we obtain sharp non-asymptotic guarantees for the existence and excess logistic risk of the MLE. We then generalize these results in two ways: first, to non-Gaussian covariates satisfying a certain two-dimensional margin condition, and second to the general case of statistical learning with a possibly misspecified logistic model. Finally, we consider the case of a Bernoulli design, where the behavior of the MLE is highly sensitive to the parameter direction.

Construction of a Surrogate Model: Multivariate Time Series Prediction with a Hybrid Model

Recent developments of advanced driver-assistance systems necessitate an increasing number of tests to validate new technologies. These tests cannot be carried out on track in a reasonable amount of time and automotive groups rely on simulators to perform most tests. The reliability of these simulators for constantly refined tasks is becoming an issue and, to increase the number of tests, the industry is now developing surrogate models, that should mimic the behavior of the simulator while being much faster to run on specific tasks. In this paper we aim to construct a surrogate model to mimic and replace the simulator. We first test several classical methods such as random forests, ridge regression or convolutional neural networks. Then we build three hybrid models that use all these methods and combine them to obtain an efficient hybrid surrogate model.

Benign overfitting in the large deviation regime

We investigate the benign overfitting phenomenon in the large deviation regime where the bounds on the prediction risk hold with probability $1-e^{-\zeta n}$, for some absolute constant $\zeta$. We prove that these bounds can converge to $0$ for the quadratic loss. We obtain this result by a new analysis of the interpolating estimator with minimal Euclidean norm, relying on a preliminary localization of this estimator with respect to the Euclidean norm. This new analysis complements and strengthens particular cases obtained in previous works for the square loss and is extended to other loss functions. To illustrate this, we also provide excess risk bounds for the Huber and absolute losses, two widely spread losses in robust statistics.

Lecture Notes: Selected topics on robust statistical learning theory

These notes gather recent results on robust statistical learning theory. The goal is to stress the main principles underlying the construction and theoretical analysis of these estimators rather than provide an exhaustive account on this rapidly growing field. The notes are the basis of lectures given at the conference StatMathAppli 2019.

Pair Matching: When bandits meet stochastic block model

The pair-matching problem appears in many applications where one wants to discover good matches between pairs of individuals. Formally, the set of individuals is represented by the nodes of a graph where the edges, unobserved at first, represent the good matches. The algorithm queries pairs of nodes and observes the presence/absence of edges. Its goal is to discover as many edges as possible with a fixed budget of queries. Pair-matching is a particular instance of multi-armed bandit problem in which the arms are pairs of individuals and the rewards are edges linking these pairs. This bandit problem is non-standard though, as each arm can only be played once. Given this last constraint, sublinear regret can be expected only if the graph presents some underlying structure. This paper shows that sublinear regret is achievable in the case where the graph is generated according to a Stochastic Block Model (SBM) with two communities. Optimal regret bounds are computed for this pair-matching problem. They exhibit a phase transition related to the Kesten-Stigund threshold for community detection in SBM. To avoid undesirable features of optimal solutions, the pair-matching problem is also considered in the case where each node is constrained to be sampled less than a given amount of times. We show how this constraint deteriorates optimal regret rates. The paper is concluded by a conjecture regarding the optimal regret when the number of communities is larger than $2$. Contrary to the two communities case, we believe that a statistical-computational gap would appear in this problem.

MONK -- Outlier-Robust Mean Embedding Estimation by Median-of-Means

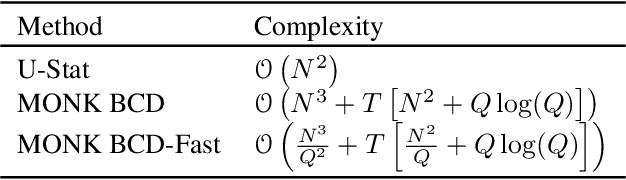
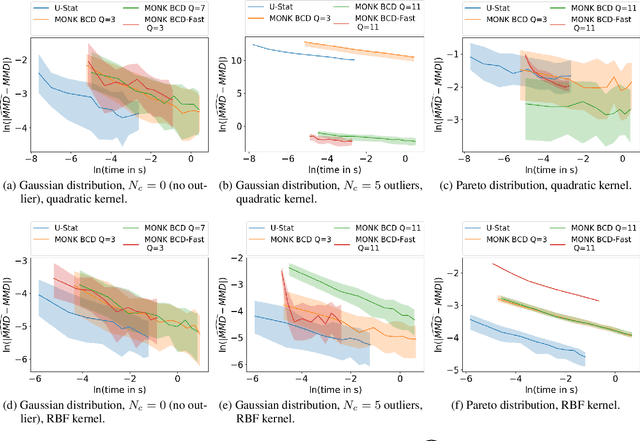
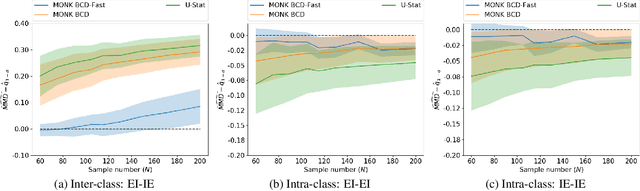
Mean embeddings provide an extremely flexible and powerful tool in machine learning and statistics to represent probability distributions and define a semi-metric (MMD, maximum mean discrepancy; also called N-distance or energy distance), with numerous successful applications. The representation is constructed as the expectation of the feature map defined by a kernel. As a mean, its classical empirical estimator, however, can be arbitrary severely affected even by a single outlier in case of unbounded features. To the best of our knowledge, unfortunately even the consistency of the existing few techniques trying to alleviate this serious sensitivity bottleneck is unknown. In this paper, we show how the recently emerged principle of median-of-means can be used to design estimators for kernel mean embedding and MMD with excessive resistance properties to outliers, and optimal sub-Gaussian deviation bounds under mild assumptions.

Choice of V for V-Fold Cross-Validation in Least-Squares Density Estimation

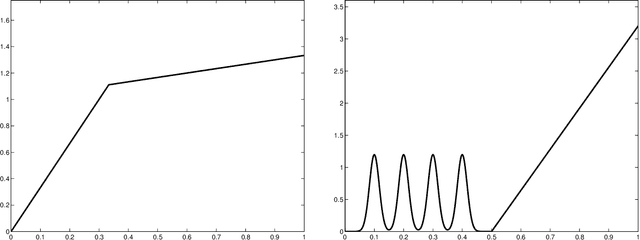
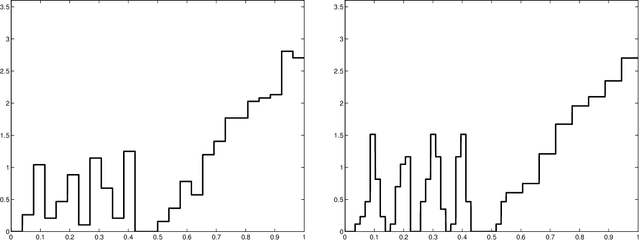
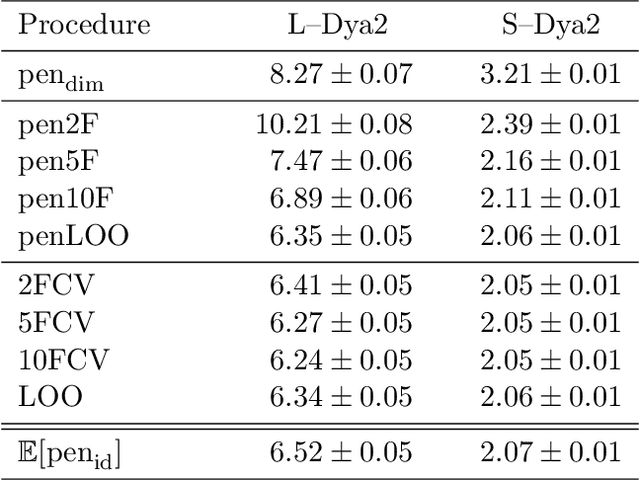
This paper studies V-fold cross-validation for model selection in least-squares density estimation. The goal is to provide theoretical grounds for choosing V in order to minimize the least-squares loss of the selected estimator. We first prove a non-asymptotic oracle inequality for V-fold cross-validation and its bias-corrected version (V-fold penalization). In particular, this result implies that V-fold penalization is asymptotically optimal in the nonparametric case. Then, we compute the variance of V-fold cross-validation and related criteria, as well as the variance of key quantities for model selection performance. We show that these variances depend on V like 1+4/(V-1), at least in some particular cases, suggesting that the performance increases much from V=2 to V=5 or 10, and then is almost constant. Overall, this can explain the common advice to take V=5---at least in our setting and when the computational power is limited---, as supported by some simulation experiments. An oracle inequality and exact formulas for the variance are also proved for Monte-Carlo cross-validation, also known as repeated cross-validation, where the parameter V is replaced by the number B of random splits of the data.