On the convergence of the MLE as an estimator of the learning rate in the Exp3 algorithm

When fitting the learning data of an individual to algorithm-like learning models, the observations are so dependent and non-stationary that one may wonder what the classical Maximum Likelihood Estimator (MLE) could do, even if it is the usual tool applied to experimental cognition. Our objective in this work is to show that the estimation of the learning rate cannot be efficient if the learning rate is constant in the classical Exp3 (Exponential weights for Exploration and Exploitation) algorithm. Secondly, we show that if the learning rate decreases polynomially with the sample size, then the prediction error and in some cases the estimation error of the MLE satisfy bounds in probability that decrease at a polynomial rate.

Disentangling Identifiable Features from Noisy Data with Structured Nonlinear ICA

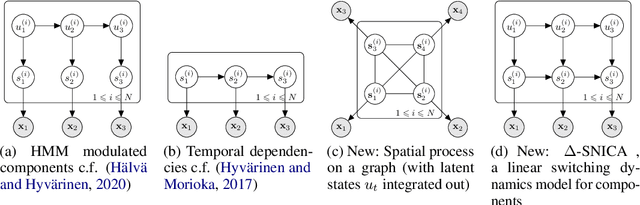
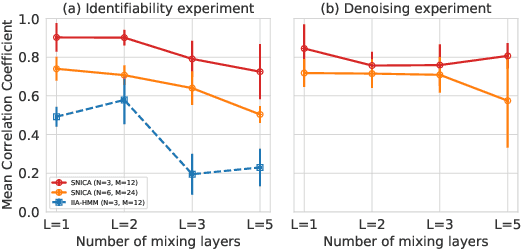
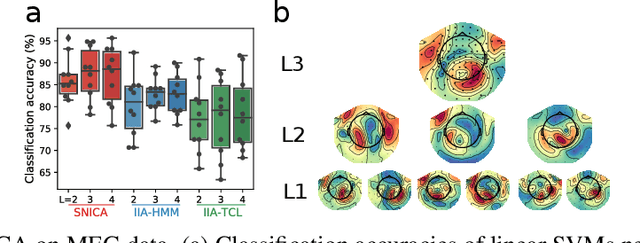
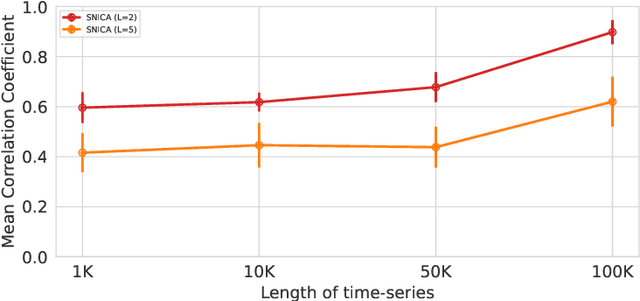
We introduce a new general identifiable framework for principled disentanglement referred to as Structured Nonlinear Independent Component Analysis (SNICA). Our contribution is to extend the identifiability theory of deep generative models for a very broad class of structured models. While previous works have shown identifiability for specific classes of time-series models, our theorems extend this to more general temporal structures as well as to models with more complex structures such as spatial dependencies. In particular, we establish the major result that identifiability for this framework holds even in the presence of noise of unknown distribution. The SNICA setting therefore subsumes all the existing nonlinear ICA models for time-series and also allows for new much richer identifiable models. Finally, as an example of our framework's flexibility, we introduce the first nonlinear ICA model for time-series that combines the following very useful properties: it accounts for both nonstationarity and autocorrelation in a fully unsupervised setting; performs dimensionality reduction; models hidden states; and enables principled estimation and inference by variational maximum-likelihood.

Joint self-supervised blind denoising and noise estimation

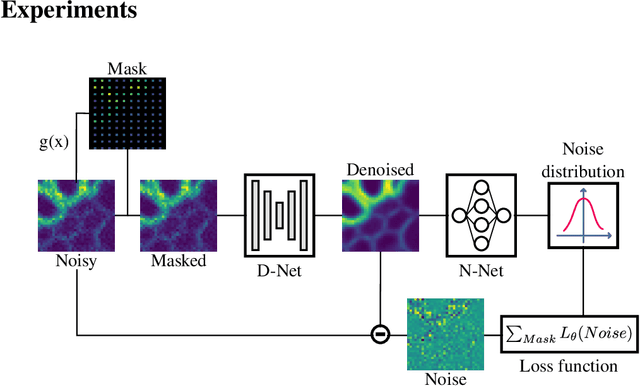
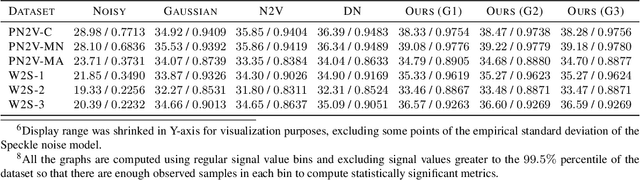
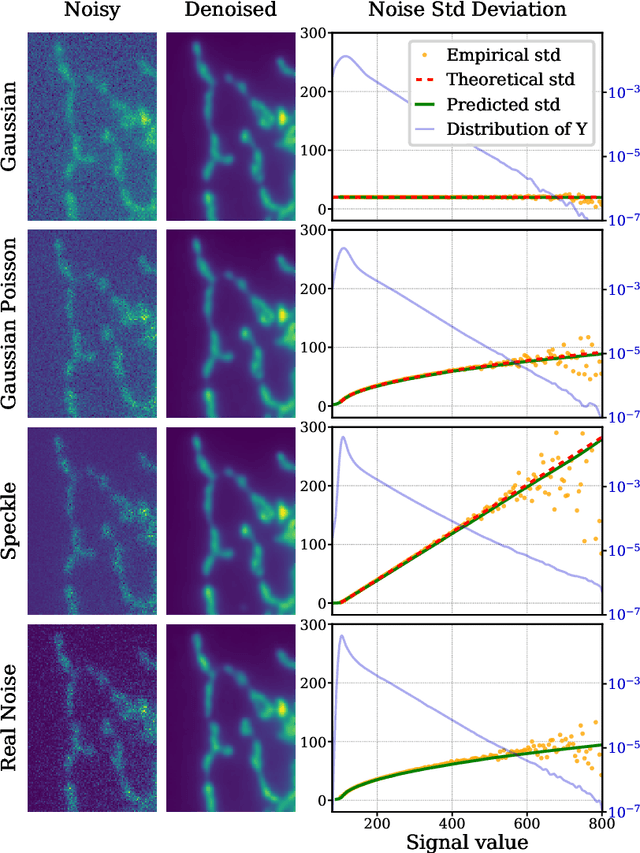
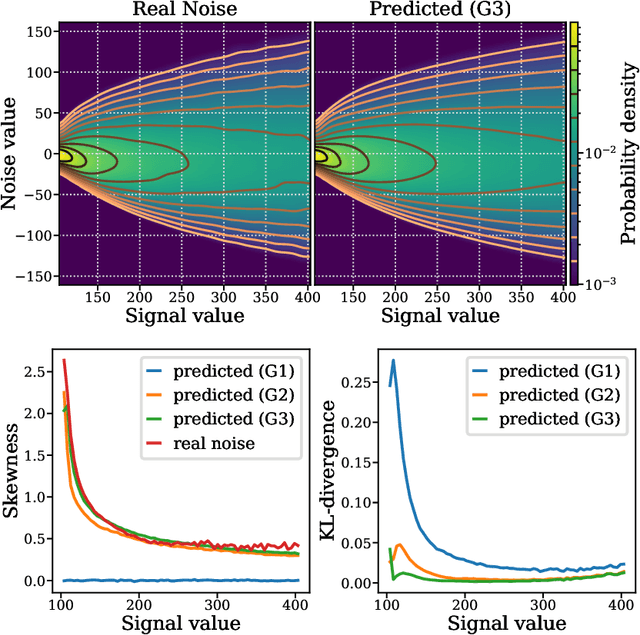
We propose a novel self-supervised image blind denoising approach in which two neural networks jointly predict the clean signal and infer the noise distribution. Assuming that the noisy observations are independent conditionally to the signal, the networks can be jointly trained without clean training data. Therefore, our approach is particularly relevant for biomedical image denoising where the noise is difficult to model precisely and clean training data are usually unavailable. Our method significantly outperforms current state-of-the-art self-supervised blind denoising algorithms, on six publicly available biomedical image datasets. We also show empirically with synthetic noisy data that our model captures the noise distribution efficiently. Finally, the described framework is simple, lightweight and computationally efficient, making it useful in practical cases.

Pair Matching: When bandits meet stochastic block model

The pair-matching problem appears in many applications where one wants to discover good matches between pairs of individuals. Formally, the set of individuals is represented by the nodes of a graph where the edges, unobserved at first, represent the good matches. The algorithm queries pairs of nodes and observes the presence/absence of edges. Its goal is to discover as many edges as possible with a fixed budget of queries. Pair-matching is a particular instance of multi-armed bandit problem in which the arms are pairs of individuals and the rewards are edges linking these pairs. This bandit problem is non-standard though, as each arm can only be played once. Given this last constraint, sublinear regret can be expected only if the graph presents some underlying structure. This paper shows that sublinear regret is achievable in the case where the graph is generated according to a Stochastic Block Model (SBM) with two communities. Optimal regret bounds are computed for this pair-matching problem. They exhibit a phase transition related to the Kesten-Stigund threshold for community detection in SBM. To avoid undesirable features of optimal solutions, the pair-matching problem is also considered in the case where each node is constrained to be sampled less than a given amount of times. We show how this constraint deteriorates optimal regret rates. The paper is concluded by a conjecture regarding the optimal regret when the number of communities is larger than $2$. Contrary to the two communities case, we believe that a statistical-computational gap would appear in this problem.