Localization in 1D non-parametric latent space models from pairwise affinities
Paper and Code
Aug 06, 2021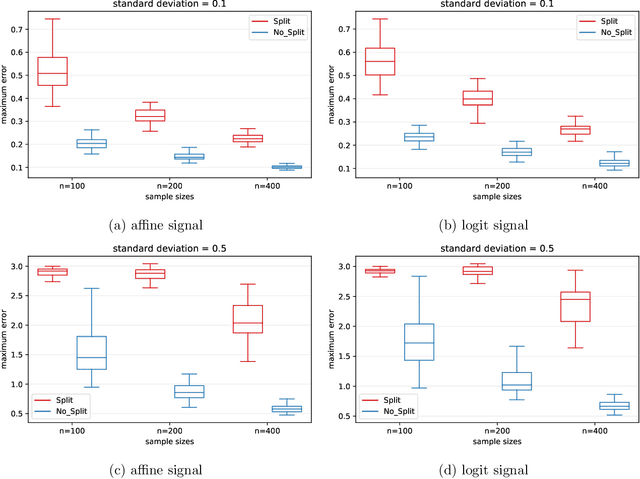
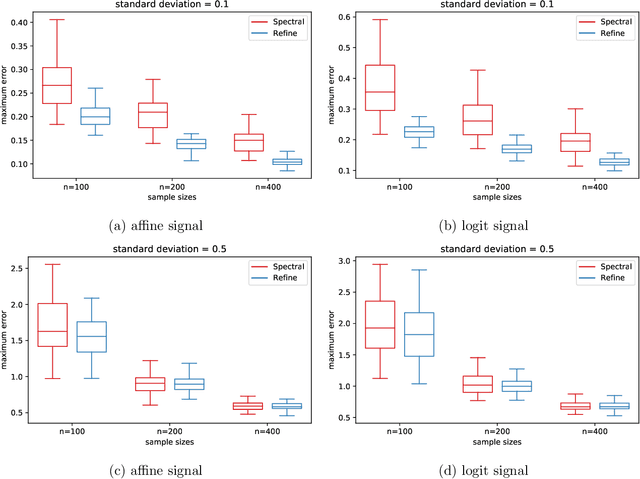
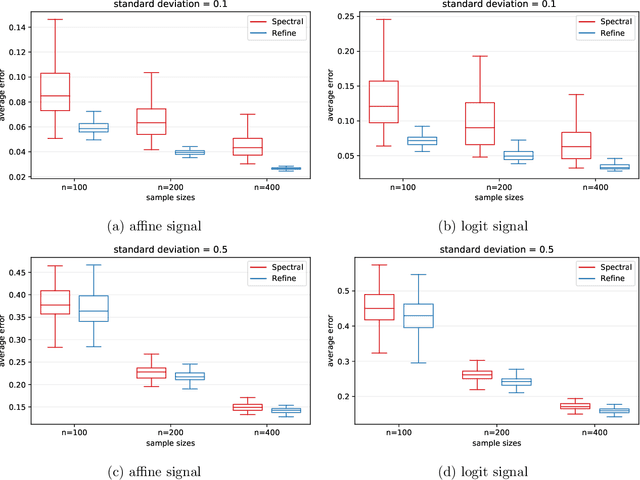
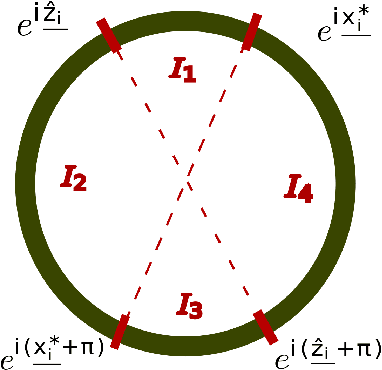
We consider the problem of estimating latent positions in a one-dimensional torus from pairwise affinities. The observed affinity between a pair of items is modeled as a noisy observation of a function $f(x^*_{i},x^*_{j})$ of the latent positions $x^*_{i},x^*_{j}$ of the two items on the torus. The affinity function $f$ is unknown, and it is only assumed to fulfill some shape constraints ensuring that $f(x,y)$ is large when the distance between $x$ and $y$ is small, and vice-versa. This non-parametric modeling offers a good flexibility to fit data. We introduce an estimation procedure that provably localizes all the latent positions with a maximum error of the order of $\sqrt{\log(n)/n}$, with high-probability. This rate is proven to be minimax optimal. A computationally efficient variant of the procedure is also analyzed under some more restrictive assumptions. Our general results can be instantiated to the problem of statistical seriation, leading to new bounds for the maximum error in the ordering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge