Robust Policy Gradient against Strong Data Corruption

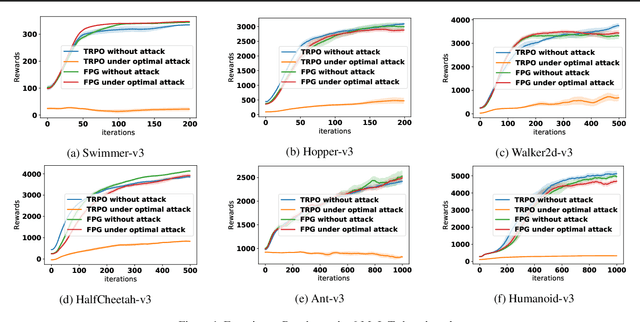
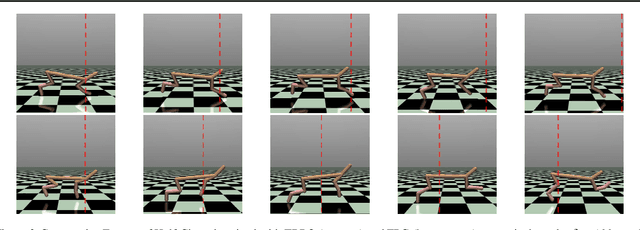
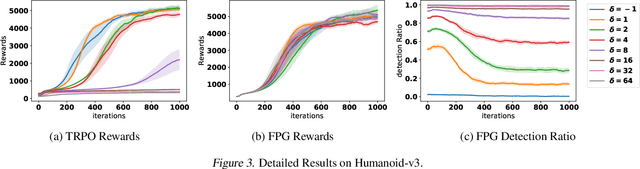
We study the problem of robust reinforcement learning under adversarial corruption on both rewards and transitions. Our attack model assumes an \textit{adaptive} adversary who can arbitrarily corrupt the reward and transition at every step within an episode, for at most $\epsilon$-fraction of the learning episodes. Our attack model is strictly stronger than those considered in prior works. Our first result shows that no algorithm can find a better than $O(\epsilon)$-optimal policy under our attack model. Next, we show that surprisingly the natural policy gradient (NPG) method retains a natural robustness property if the reward corruption is bounded, and can find an $O(\sqrt{\epsilon})$-optimal policy. Consequently, we develop a Filtered Policy Gradient (FPG) algorithm that can tolerate even unbounded reward corruption and can find an $O(\epsilon^{1/4})$-optimal policy. We emphasize that FPG is the first that can achieve a meaningful learning guarantee when a constant fraction of episodes are corrupted. Complimentary to the theoretical results, we show that a neural implementation of FPG achieves strong robust learning performance on the MuJoCo continuous control benchmarks.

Using Machine Teaching to Investigate Human Assumptions when Teaching Reinforcement Learners

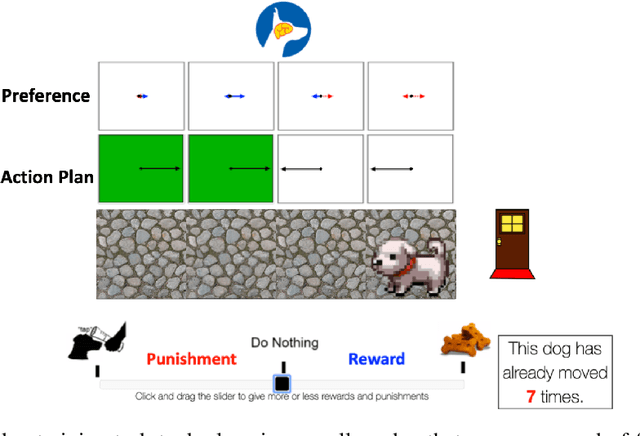
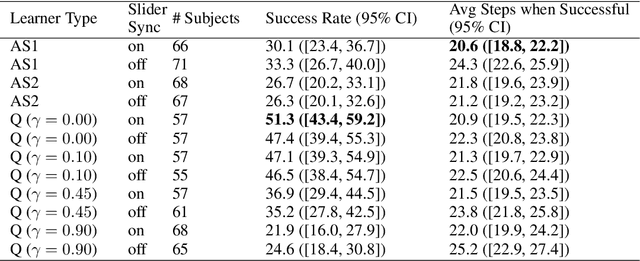
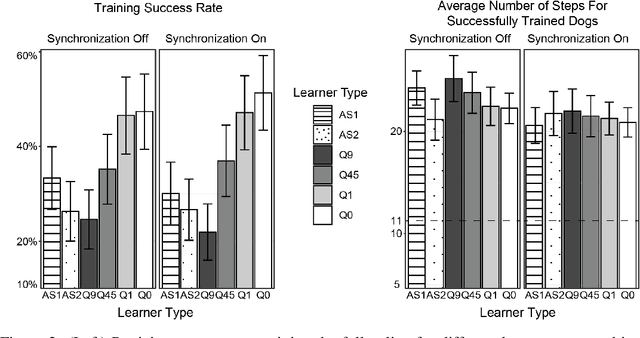
Successful teaching requires an assumption of how the learner learns - how the learner uses experiences from the world to update their internal states. We investigate what expectations people have about a learner when they teach them in an online manner using rewards and punishment. We focus on a common reinforcement learning method, Q-learning, and examine what assumptions people have using a behavioral experiment. To do so, we first establish a normative standard, by formulating the problem as a machine teaching optimization problem. To solve the machine teaching optimization problem, we use a deep learning approximation method which simulates learners in the environment and learns to predict how feedback affects the learner's internal states. What do people assume about a learner's learning and discount rates when they teach them an idealized exploration-exploitation task? In a behavioral experiment, we find that people can teach the task to Q-learners in a relatively efficient and effective manner when the learner uses a small value for its discounting rate and a large value for its learning rate. However, they still are suboptimal. We also find that providing people with real-time updates of how possible feedback would affect the Q-learner's internal states weakly helps them teach. Our results reveal how people teach using evaluative feedback and provide guidance for how engineers should design machine agents in a manner that is intuitive for people.

Task-agnostic Exploration in Reinforcement Learning

Efficient exploration is one of the main challenges in reinforcement learning (RL). Most existing sample-efficient algorithms assume the existence of a single reward function during exploration. In many practical scenarios, however, there is not a single underlying reward function to guide the exploration, for instance, when an agent needs to learn many skills simultaneously, or multiple conflicting objectives need to be balanced. To address these challenges, we propose the \textit{task-agnostic RL} framework: In the exploration phase, the agent first collects trajectories by exploring the MDP without the guidance of a reward function. After exploration, it aims at finding near-optimal policies for $N$ tasks, given the collected trajectories augmented with \textit{sampled rewards} for each task. We present an efficient task-agnostic RL algorithm, \textsc{UCBZero}, that finds $\epsilon$-optimal policies for $N$ arbitrary tasks after at most $\tilde O(\log(N)H^5SA/\epsilon^2)$ exploration episodes. We also provide an $\Omega(\log (N)H^2SA/\epsilon^2)$ lower bound, showing that the $\log$ dependency on $N$ is unavoidable. Furthermore, we provide an $N$-independent sample complexity bound of \textsc{UCBZero} in the statistically easier setting when the ground truth reward functions are known.

The Teaching Dimension of Q-learning

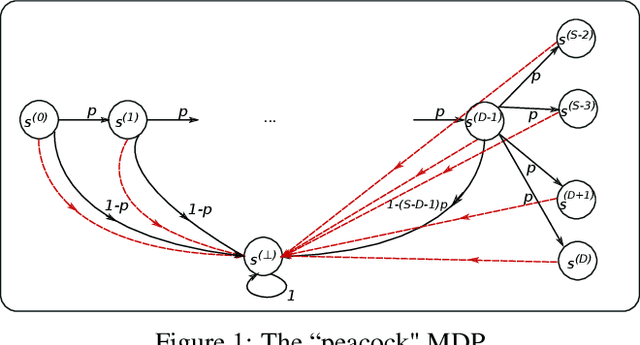
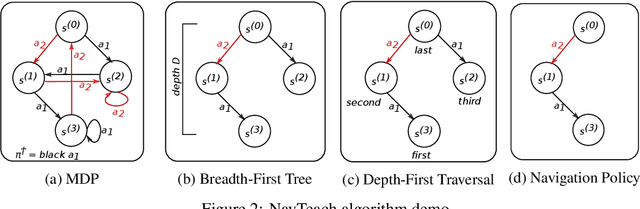
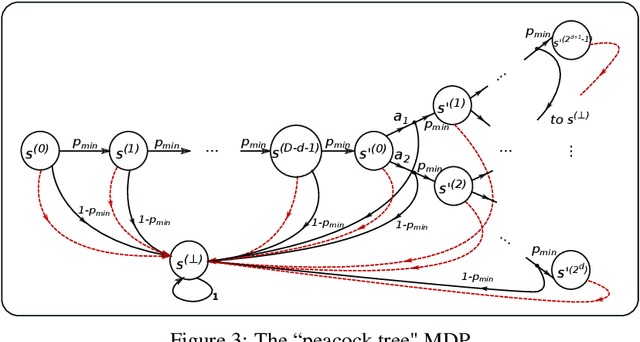
In this paper, we initiate the study of sample complexity of teaching, termed as "teaching dimension" (TDim) in the literature, for Q-learning. While the teaching dimension of supervised learning has been studied extensively, these results do not extend to reinforcement learning due to the temporal constraints posed by the underlying Markov Decision Process environment. We characterize the TDim of Q-learning under different teachers with varying control over the environment, and present matching optimal teaching algorithms. Our TDim results provide the minimum number of samples needed for reinforcement learning, thus complementing standard PAC-style RL sample complexity analysis. Our teaching algorithms have the potential to speed up RL agent learning in applications where a helpful teacher is available.

Neural Additive Models: Interpretable Machine Learning with Neural Nets

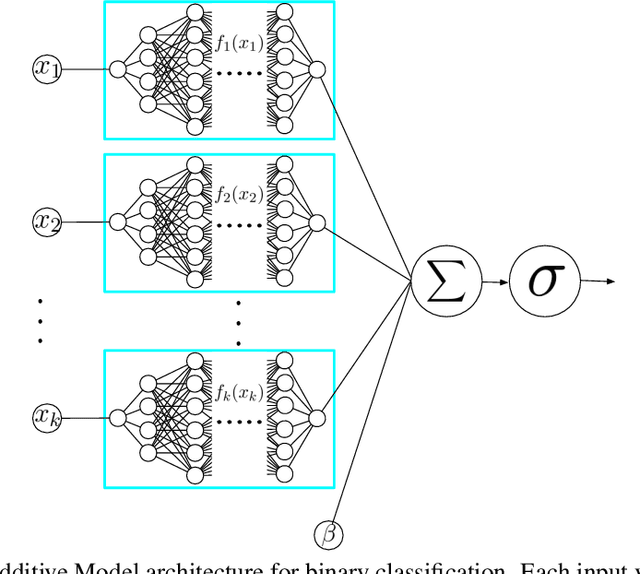
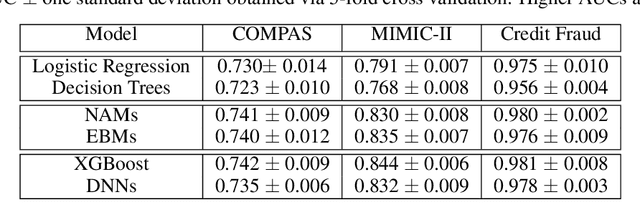
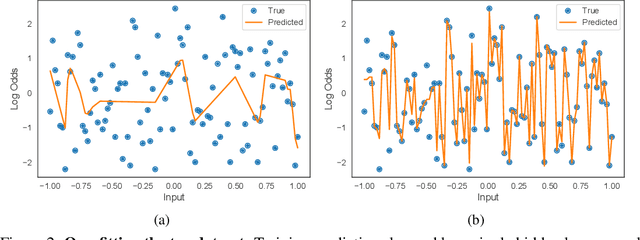
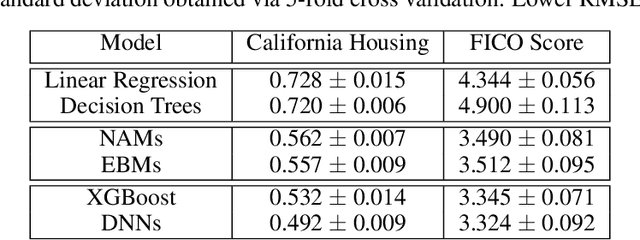
Deep neural networks (DNNs) are powerful black-box predictors that have achieved impressive performance on a wide variety of tasks. However, their accuracy comes at the cost of intelligibility: it is usually unclear how they make their decisions. This hinders their applicability to high stakes decision-making domains such as healthcare. We propose Neural Additive Models (NAMs) which combine some of the expressivity of DNNs with the inherent intelligibility of generalized additive models. NAMs learn a linear combination of neural networks that each attend to a single input feature. These networks are trained jointly and can learn arbitrarily complex relationships between their input feature and the output. Our experiments on regression and classification datasets show that NAMs are more accurate than widely used intelligible models such as logistic regression and shallow decision trees. They perform similarly to existing state-of-the-art generalized additive models in accuracy, but can be more easily applied to real-world problems.

Adaptive Reward-Poisoning Attacks against Reinforcement Learning

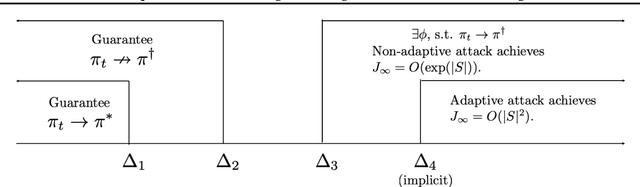
In reward-poisoning attacks against reinforcement learning (RL), an attacker can perturb the environment reward $r_t$ into $r_t+\delta_t$ at each step, with the goal of forcing the RL agent to learn a nefarious policy. We categorize such attacks by the infinity-norm constraint on $\delta_t$: We provide a lower threshold below which reward-poisoning attack is infeasible and RL is certified to be safe; we provide a corresponding upper threshold above which the attack is feasible. Feasible attacks can be further categorized as non-adaptive where $\delta_t$ depends only on $(s_t,a_t, s_{t+1})$, or adaptive where $\delta_t$ depends further on the RL agent's learning process at time $t$. Non-adaptive attacks have been the focus of prior works. However, we show that under mild conditions, adaptive attacks can achieve the nefarious policy in steps polynomial in state-space size $|S|$, whereas non-adaptive attacks require exponential steps. We provide a constructive proof that a Fast Adaptive Attack strategy achieves the polynomial rate. Finally, we show that empirically an attacker can find effective reward-poisoning attacks using state-of-the-art deep RL techniques.

Policy Poisoning in Batch Reinforcement Learning and Control

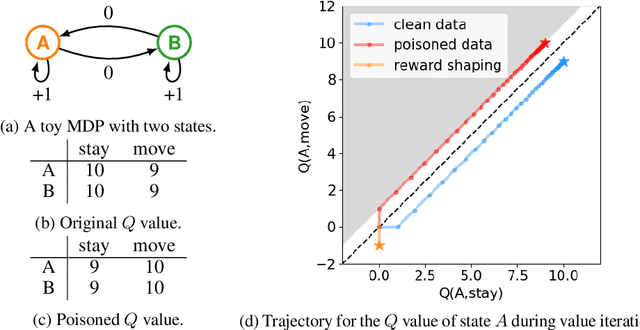
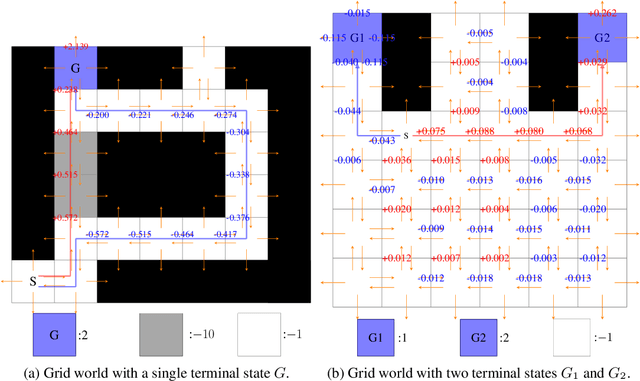
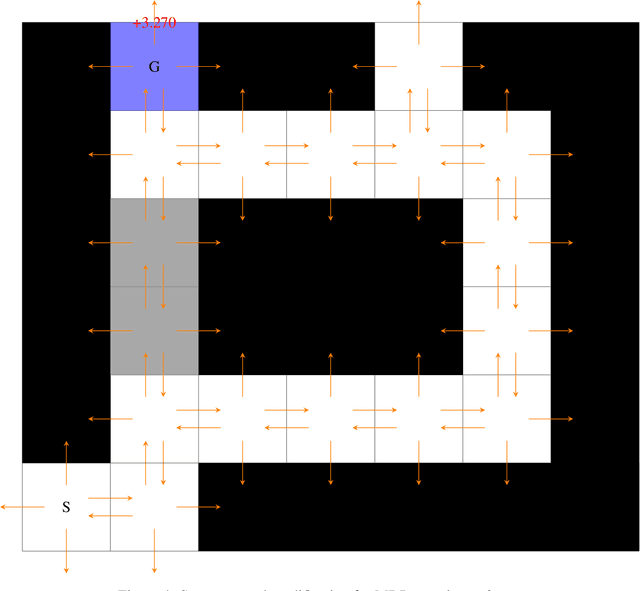
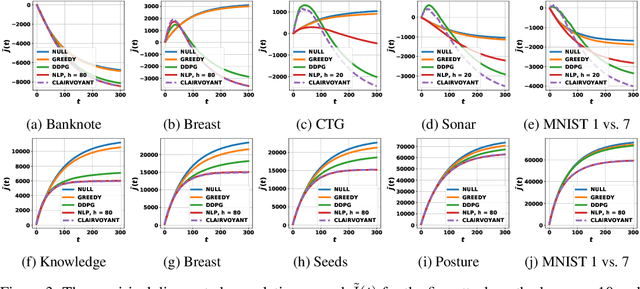
We study a security threat to batch reinforcement learning and control where the attacker aims to poison the learned policy. The victim is a reinforcement learner / controller which first estimates the dynamics and the rewards from a batch data set, and then solves for the optimal policy with respect to the estimates. The attacker can modify the data set slightly before learning happens, and wants to force the learner into learning a target policy chosen by the attacker. We present a unified framework for solving batch policy poisoning attacks, and instantiate the attack on two standard victims: tabular certainty equivalence learner in reinforcement learning and linear quadratic regulator in control. We show that both instantiation result in a convex optimization problem on which global optimality is guaranteed, and provide analysis on attack feasibility and attack cost. Experiments show the effectiveness of policy poisoning attacks.

Online Data Poisoning Attack

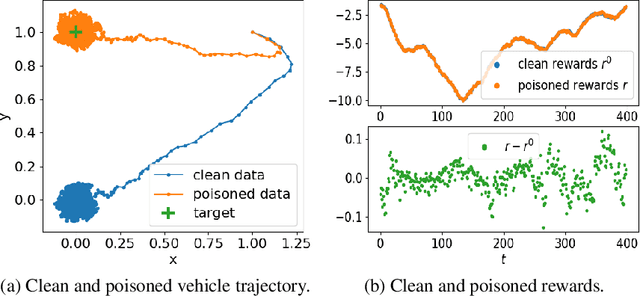
We study data poisoning attacks in the online learning setting where the training items stream in one at a time, and the adversary perturbs the current training item to manipulate present and future learning. In contrast, prior work on data poisoning attacks has focused on either batch learners in the offline setting, or online learners but with full knowledge of the whole training sequence. We show that online poisoning attack can be formulated as stochastic optimal control, and provide several practical attack algorithms based on control and deep reinforcement learning. Extensive experiments demonstrate the effectiveness of the attacks.

Interpretability is Harder in the Multiclass Setting: Axiomatic Interpretability for Multiclass Additive Models

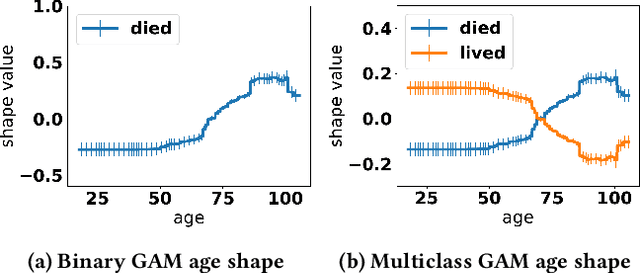
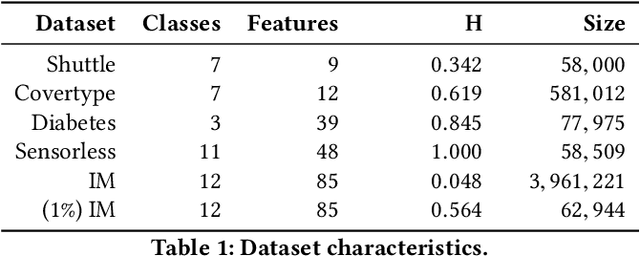
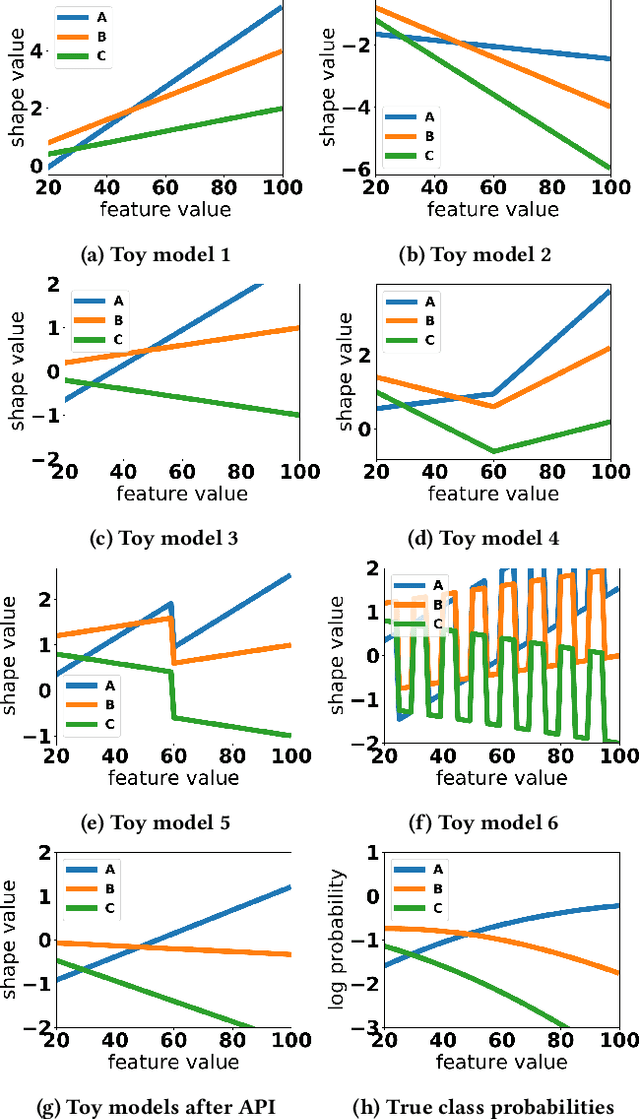
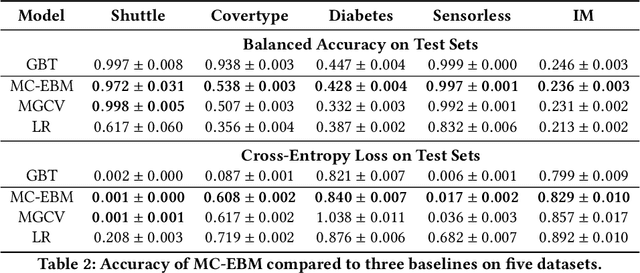
Generalized additive models (GAMs) are favored in many regression and binary classification problems because they are able to fit complex, nonlinear functions while still remaining interpretable. In the first part of this paper, we generalize a state-of-the-art GAM learning algorithm based on boosted trees to the multiclass setting, and show that this multiclass algorithm outperforms existing GAM fitting algorithms and sometimes matches the performance of full complex models. In the second part, we turn our attention to the interpretability of GAMs in the multiclass setting. Surprisingly, the natural interpretability of GAMs breaks down when there are more than two classes. Drawing inspiration from binary GAMs, we identify two axioms that any additive model must satisfy to not be visually misleading. We then develop a post-processing technique (API) that provably transforms pretrained additive models to satisfy the interpretability axioms without sacrificing accuracy. The technique works not just on models trained with our algorithm, but on any multiclass additive model. We demonstrate API on a 12-class infant-mortality dataset.

An Optimal Control Approach to Sequential Machine Teaching

Given a sequential learning algorithm and a target model, sequential machine teaching aims to find the shortest training sequence to drive the learning algorithm to the target model. We present the first principled way to find such shortest training sequences. Our key insight is to formulate sequential machine teaching as a time-optimal control problem. This allows us to solve sequential teaching by leveraging key theoretical and computational tools developed over the past 60 years in the optimal control community. Specifically, we study the Pontryagin Maximum Principle, which yields a necessary condition for optimality of a training sequence. We present analytic, structural, and numerical implications of this approach on a case study with a least-squares loss function and gradient descent learner. We compute optimal training sequences for this problem, and although the sequences seem circuitous, we find that they can vastly outperform the best available heuristics for generating training sequences.