Learning to Manipulate a Commitment Optimizer

It is shown in recent studies that in a Stackelberg game the follower can manipulate the leader by deviating from their true best-response behavior. Such manipulations are computationally tractable and can be highly beneficial for the follower. Meanwhile, they may result in significant payoff losses for the leader, sometimes completely defeating their first-mover advantage. A warning to commitment optimizers, the risk these findings indicate appears to be alleviated to some extent by a strict information advantage the manipulations rely on. That is, the follower knows the full information about both players' payoffs whereas the leader only knows their own payoffs. In this paper, we study the manipulation problem with this information advantage relaxed. We consider the scenario where the follower is not given any information about the leader's payoffs to begin with but has to learn to manipulate by interacting with the leader. The follower can gather necessary information by querying the leader's optimal commitments against contrived best-response behaviors. Our results indicate that the information advantage is not entirely indispensable to the follower's manipulations: the follower can learn the optimal way to manipulate in polynomial time with polynomially many queries of the leader's optimal commitment.

Are Equivariant Equilibrium Approximators Beneficial?

Recently, remarkable progress has been made by approximating Nash equilibrium (NE), correlated equilibrium (CE), and coarse correlated equilibrium (CCE) through function approximation that trains a neural network to predict equilibria from game representations. Furthermore, equivariant architectures are widely adopted in designing such equilibrium approximators in normal-form games. In this paper, we theoretically characterize benefits and limitations of equivariant equilibrium approximators. For the benefits, we show that they enjoy better generalizability than general ones and can achieve better approximations when the payoff distribution is permutation-invariant. For the limitations, we discuss their drawbacks in terms of equilibrium selection and social welfare. Together, our results help to understand the role of equivariance in equilibrium approximators.

On the Re-Solving Heuristic for Contextual Bandits with Knapsacks

In the problem of (binary) contextual bandits with knapsacks (CBwK), the agent receives an i.i.d. context in each of the $T$ rounds and chooses an action, resulting in a random reward and a random consumption of resources that are related to an i.i.d. external factor. The agent's goal is to maximize the accumulated reward under the initial resource constraints. In this work, we combine the re-solving heuristic, which proved successful in revenue management, with distribution estimation techniques to solve this problem. We consider two different information feedback models, with full and partial information, which vary in the difficulty of getting a sample of the external factor. Under both information feedback settings, we achieve two-way results: (1) For general problems, we show that our algorithm gets an $\widetilde O(T^{\alpha_u} + T^{\alpha_v} + T^{1/2})$ regret against the fluid benchmark. Here, $\alpha_u$ and $\alpha_v$ reflect the complexity of the context and external factor distributions, respectively. This result is comparable to existing results. (2) When the fluid problem is linear programming with a unique and non-degenerate optimal solution, our algorithm leads to an $\widetilde O(1)$ regret. To the best of our knowledge, this is the first $\widetilde O(1)$ regret result in the CBwK problem regardless of information feedback models. We further use numerical experiments to verify our results.

Sybil-Proof Diffusion Auction in Social Networks

A diffusion auction is a market to sell commodities over a social network, where the challenge is to incentivize existing buyers to invite their neighbors in the network to join the market. Existing mechanisms have been designed to solve the challenge in various settings, aiming at desirable properties such as non-deficiency, incentive compatibility and social welfare maximization. Since the mechanisms are employed in dynamic networks with ever-changing structures, buyers could easily generate fake nodes in the network to manipulate the mechanisms for their own benefits, which is commonly known as the Sybil attack. We observe that strategic agents may gain an unfair advantage in existing mechanisms through such attacks. To resist this potential attack, we propose two diffusion auction mechanisms, the Sybil tax mechanism (STM) and the Sybil cluster mechanism (SCM), to achieve both Sybil-proofness and incentive compatibility in the single-item setting. Our proposal provides the first mechanisms to protect the interests of buyers against Sybil attacks with a mild sacrifice of social welfare and revenue.

Dynamic Budget Throttling in Repeated Second-Price Auctions

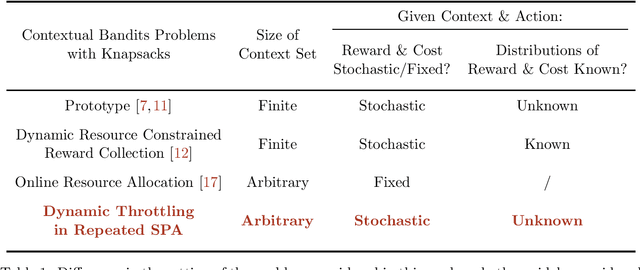
Throttling is one of the most popular budget control methods in today's online advertising markets. When a budget-constrained advertiser employs throttling, she can choose whether or not to participate in an auction after the advertising platform recommends a bid. This paper focuses on the dynamic budget throttling process in repeated second-price auctions from a theoretical view. An essential feature of the underlying problem is that the advertiser does not know the distribution of the highest competing bid upon entering the market. To model the difficulty of eliminating such uncertainty, we consider two different information structures. The advertiser could obtain the highest competing bid in each round with full-information feedback. Meanwhile, with partial information feedback, the advertiser could only have access to the highest competing bid in the auctions she participates in. We propose the OGD-CB algorithm, which involves simultaneous distribution learning and revenue optimization. In both settings, we demonstrate that this algorithm guarantees an $O(\sqrt{T\log T})$ regret with probability $1 - O(1/T)$ relative to the fluid adaptive throttling benchmark. By proving a lower bound of $\Omega(\sqrt{T})$ on the minimal regret for even the hindsight optimum, we establish the near optimality of our algorithm. Finally, we compare the fluid optimum of throttling to that of pacing, another widely adopted budget control method. The numerical relationship of these benchmarks sheds new light on the understanding of different online algorithms for revenue maximization under budget constraints.

Optimal Private Payoff Manipulation against Commitment in Extensive-form Games

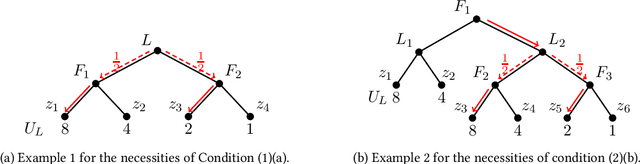
To take advantage of strategy commitment, a useful tactic of playing games, a leader must learn enough information about the follower's payoff function. However, this leaves the follower a chance to provide fake information and influence the final game outcome. Through a carefully contrived payoff function misreported to the learning leader, the follower may induce an outcome that benefits him more, compared to the ones when he truthfully behaves. We study the follower's optimal manipulation via such strategic behaviors in extensive-form games. Followers' different attitudes are taken into account. An optimistic follower maximizes his true utility among all game outcomes that can be induced by some payoff function. A pessimistic follower only considers misreporting payoff functions that induce a unique game outcome. For all the settings considered in this paper, we characterize all the possible game outcomes that can be induced successfully. We show that it is polynomial-time tractable for the follower to find the optimal way of misreporting his private payoff information. Our work completely resolves this follower's optimal manipulation problem on an extensive-form game tree.

No-regret Learning in Repeated First-Price Auctions with Budget Constraints

Recently the online advertising market has exhibited a gradual shift from second-price auctions to first-price auctions. Although there has been a line of works concerning online bidding strategies in first-price auctions, it still remains open how to handle budget constraints in the problem. In the present paper, we initiate the study for a buyer with budgets to learn online bidding strategies in repeated first-price auctions. We propose an RL-based bidding algorithm against the optimal non-anticipating strategy under stationary competition. Our algorithm obtains $\widetilde O(\sqrt T)$-regret if the bids are all revealed at the end of each round. With the restriction that the buyer only sees the winning bid after each round, our modified algorithm obtains $\widetilde O(T^{\frac{7}{12}})$-regret by techniques developed from survival analysis. Our analysis extends to the more general scenario where the buyer has any bounded instantaneous utility function with regrets of the same order.

On the Convergence of Fictitious Play: A Decomposition Approach

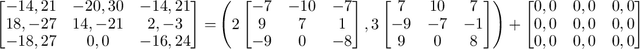
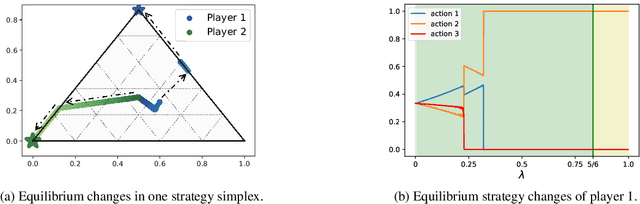
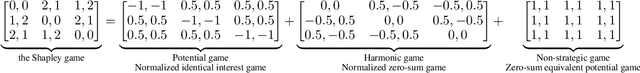
Fictitious play (FP) is one of the most fundamental game-theoretical learning frameworks for computing Nash equilibrium in $n$-player games, which builds the foundation for modern multi-agent learning algorithms. Although FP has provable convergence guarantees on zero-sum games and potential games, many real-world problems are often a mixture of both and the convergence property of FP has not been fully studied yet. In this paper, we extend the convergence results of FP to the combinations of such games and beyond. Specifically, we derive new conditions for FP to converge by leveraging game decomposition techniques. We further develop a linear relationship unifying cooperation and competition in the sense that these two classes of games are mutually transferable. Finally, we analyze a non-convergent example of FP, the Shapley game, and develop sufficient conditions for FP to converge.

Characterizing Parametric and Convergence Stability in Nonconvex and Nonsmooth Optimizations: A Geometric Approach

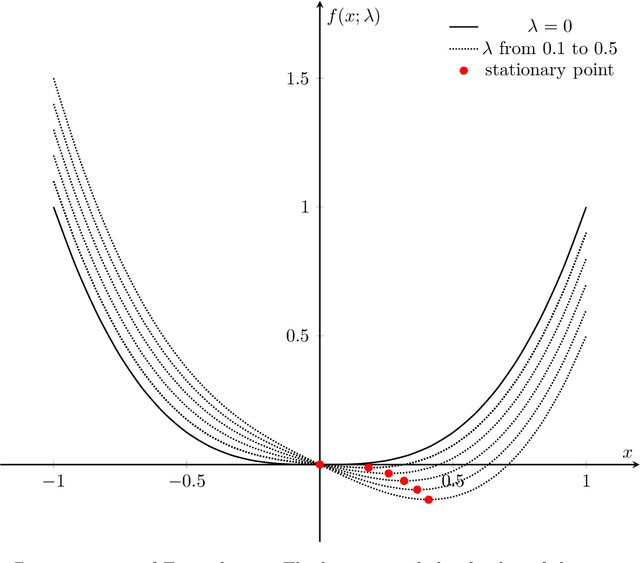
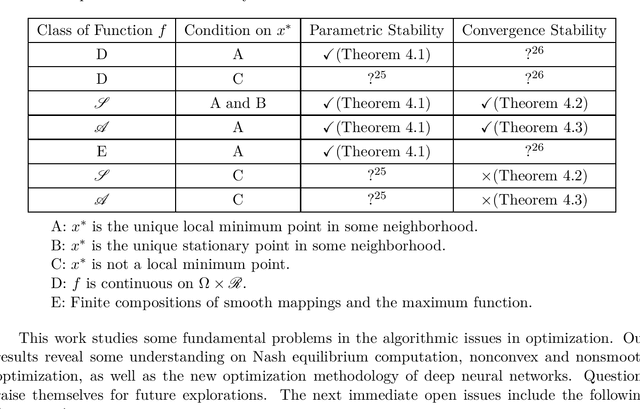
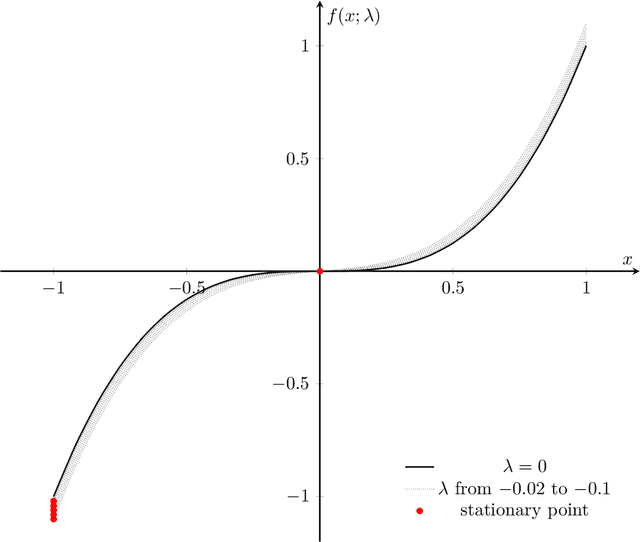
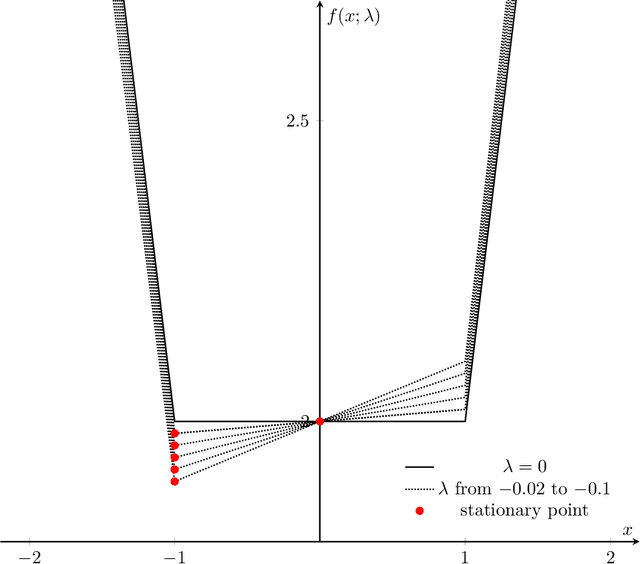
We consider stability issues in minimizing a continuous (probably parameterized, nonconvex and nonsmooth) real-valued function $f$. We call a point stationary if all its possible directional derivatives are nonnegative. In this work, we focus on two notions of stability on stationary points of $f$: parametric stability and convergence stability. Parametric considerations are widely studied in various fields, including smoothed analysis, numerical stability, condition numbers and sensitivity analysis for linear programming. Parametric stability asks whether minor perturbations on parameters lead to dramatic changes in the position and $f$ value of a stationary point. Meanwhile, convergence stability indicates a non-escapable solution: Any point sequence iteratively produced by an optimization algorithm cannot escape from a neighborhood of a stationary point but gets close to it in the sense that such stationary points are stable to the precision parameter and algorithmic numerical errors. It turns out that these notions have deep connections to geometry theory. We show that parametric stability is linked to deformations of graphs of functions. On the other hand, convergence stability is concerned with area partitioning of the function domain. Utilizing these connections, we prove quite tight conditions of these two stability notions for a wide range of functions and optimization algorithms with small enough step sizes and precision parameters. These conditions are subtle in the sense that a slightly weaker function requirement goes to the opposite of primitive intuitions and leads to wrong conclusions. We present three applications of this theory. These applications reveal some understanding on Nash equilibrium computation, nonconvex and nonsmooth optimization, as well as the new optimization methodology of deep neural networks.

A Context-Integrated Transformer-Based Neural Network for Auction Design

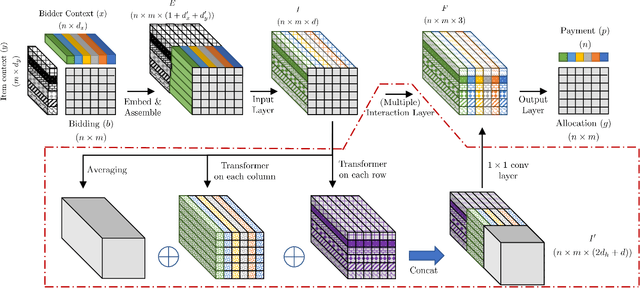
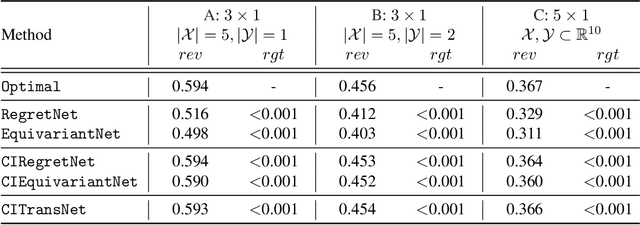
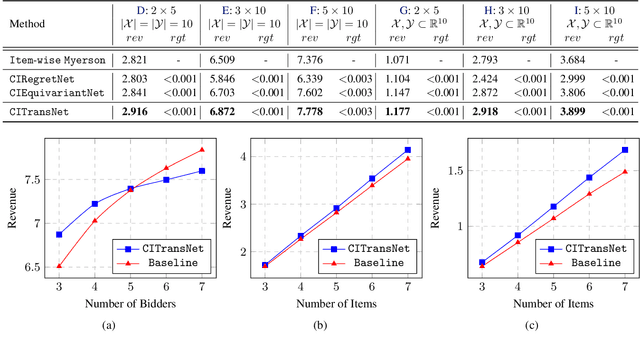
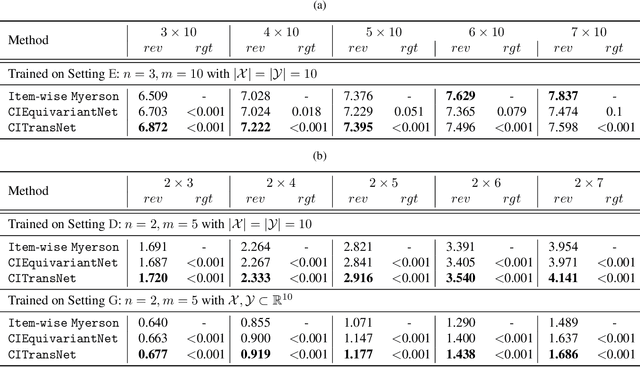
One of the central problems in auction design is developing an incentive-compatible mechanism that maximizes the auctioneer's expected revenue. While theoretical approaches have encountered bottlenecks in multi-item auctions, recently, there has been much progress on finding the optimal mechanism through deep learning. However, these works either focus on a fixed set of bidders and items, or restrict the auction to be symmetric. In this work, we overcome such limitations by factoring \emph{public} contextual information of bidders and items into the auction learning framework. We propose $\mathtt{CITransNet}$, a context-integrated transformer-based neural network for optimal auction design, which maintains permutation-equivariance over bids and contexts while being able to find asymmetric solutions. We show by extensive experiments that $\mathtt{CITransNet}$ can recover the known optimal solutions in single-item settings, outperform strong baselines in multi-item auctions, and generalize well to cases other than those in training.