Robust Categorical Data Clustering Guided by Multi-Granular Competitive Learning

Data set composed of categorical features is very common in big data analysis tasks. Since categorical features are usually with a limited number of qualitative possible values, the nested granular cluster effect is prevalent in the implicit discrete distance space of categorical data. That is, data objects frequently overlap in space or subspace to form small compact clusters, and similar small clusters often form larger clusters. However, the distance space cannot be well-defined like the Euclidean distance due to the qualitative categorical data values, which brings great challenges to the cluster analysis of categorical data. In view of this, we design a Multi-Granular Competitive Penalization Learning (MGCPL) algorithm to allow potential clusters to interactively tune themselves and converge in stages with different numbers of naturally compact clusters. To leverage MGCPL, we also propose a Cluster Aggregation strategy based on MGCPL Encoding (CAME) to first encode the data objects according to the learned multi-granular distributions, and then perform final clustering on the embeddings. It turns out that the proposed MGCPL-guided Categorical Data Clustering (MCDC) approach is competent in automatically exploring the nested distribution of multi-granular clusters and highly robust to categorical data sets from various domains. Benefiting from its linear time complexity, MCDC is scalable to large-scale data sets and promising in pre-partitioning data sets or compute nodes for boosting distributed computing. Extensive experiments with statistical evidence demonstrate its superiority compared to state-of-the-art counterparts on various real public data sets.

HMVI: Unifying Heterogeneous Attributes with Natural Neighbors for Missing Value Inference

Missing value imputation is a fundamental challenge in machine intelligence, heavily dependent on data completeness. Current imputation methods often handle numerical and categorical attributes independently, overlooking critical interdependencies among heterogeneous features. To address these limitations, we propose a novel imputation approach that explicitly models cross-type feature dependencies within a unified framework. Our method leverages both complete and incomplete instances to ensure accurate and consistent imputation in tabular data. Extensive experimental results demonstrate that the proposed approach achieves superior performance over existing techniques and significantly enhances downstream machine learning tasks, providing a robust solution for real-world systems with missing data.

A New Accelerated Stochastic Gradient Method with Momentum

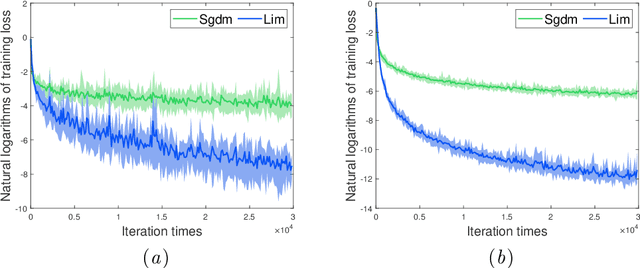
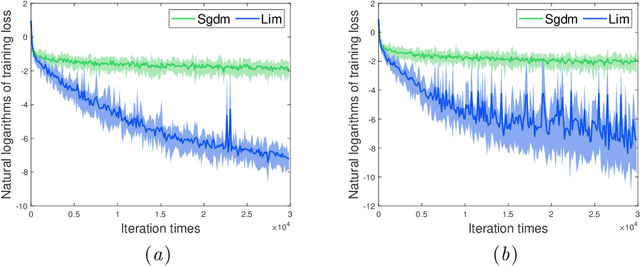
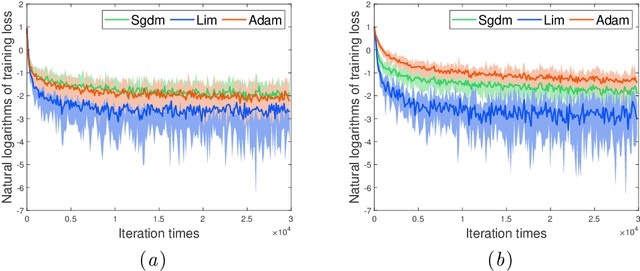
In this paper, we propose a novel accelerated stochastic gradient method with momentum, which momentum is the weighted average of previous gradients. The weights decays inverse proportionally with the iteration times. Stochastic gradient descent with momentum (Sgdm) use weights that decays exponentially with the iteration times to generate an momentum term. Using exponentially decaying weights, variants of Sgdm with well designed and complicated formats have been proposed to achieve better performance. The momentum update rules of our method is as simple as that of Sgdm. We provide theoretical convergence properties analyses for our method, which show both the exponentially decay weights and our inverse proportionally decay weights can limit the variance of the moving direction of parameters to be optimized to a region. Experimental results empirically show that our method works well with practical problems and outperforms Sgdm, and it outperforms Adam in convolutional neural networks.

Can speed up the convergence rate of stochastic gradient methods to $\mathcal{O}$ by a gradient averaging strategy?

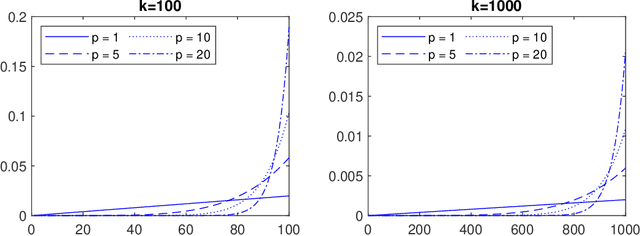
In this paper we consider the question of whether it is possible to apply a gradient averaging strategy to improve on the sublinear convergence rates without any increase in storage. Our analysis reveals that a positive answer requires an appropriate averaging strategy and iterations that satisfy the variance dominant condition. As an interesting fact, we show that if the iterative variance we defined is always dominant even a little bit in the stochastic gradient iterations, the proposed gradient averaging strategy can increase the convergence rate $\mathcal{O}(1/k)$ to $\mathcal{O}(1/k^2)$ in probability for the strongly convex objectives with Lipschitz gradients. This conclusion suggests how we should control the stochastic gradient iterations to improve the rate of convergence.

Stochastic gradient-free descents

In this paper we propose stochastic gradient-free methods and accelerated methods with momentum for solving stochastic optimization problems. All these methods rely on stochastic directions rather than stochastic gradients. We analyze the convergence behavior of these methods under the mean-variance framework, and also provide a theoretical analysis about the inclusion of momentum in stochastic settings which reveals that the momentum term we used adds a deviation of order $\mathcal{O}(1/k)$ but controls the variance at the order $\mathcal{O}(1/k)$ for the $k$th iteration. So it is shown that, when employing a decaying stepsize $\alpha_k=\mathcal{O}(1/k)$, the stochastic gradient-free methods can still maintain the sublinear convergence rate $\mathcal{O}(1/k)$ and the accelerated methods with momentum can achieve a convergence rate $\mathcal{O}(1/k^2)$ in probability for the strongly convex objectives with Lipschitz gradients; and all these methods converge to a solution with a zero expected gradient norm when the objective function is nonconvex, twice differentiable and bounded below.