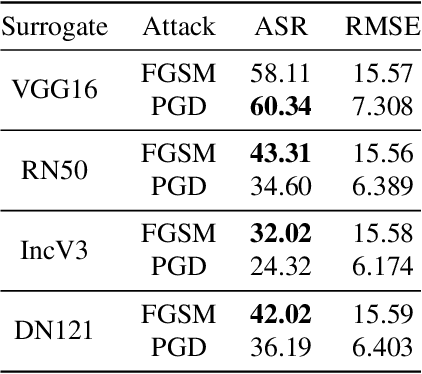
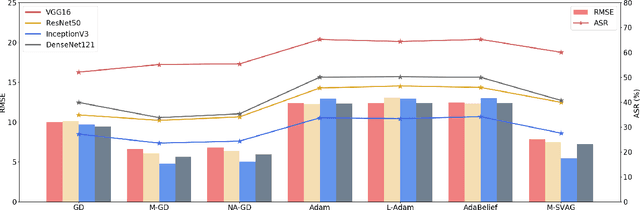
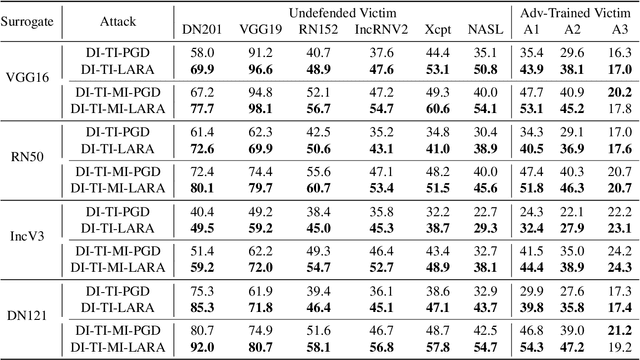
Going Far Boosts Attack Transferability, but Do Not Do It

Deep Neural Networks (DNNs) could be easily fooled by Adversarial Examples (AEs) with an imperceptible difference to original ones in human eyes. Also, the AEs from attacking one surrogate DNN tend to cheat other black-box DNNs as well, i.e., the attack transferability. Existing works reveal that adopting certain optimization algorithms in attack improves transferability, but the underlying reasons have not been thoroughly studied. In this paper, we investigate the impacts of optimization on attack transferability by comprehensive experiments concerning 7 optimization algorithms, 4 surrogates, and 9 black-box models. Through the thorough empirical analysis from three perspectives, we surprisingly find that the varied transferability of AEs from optimization algorithms is strongly related to the corresponding Root Mean Square Error (RMSE) from their original samples. On such a basis, one could simply approach high transferability by attacking until RMSE decreases, which motives us to propose a LArge RMSE Attack (LARA). Although LARA significantly improves transferability by 20%, it is insufficient to exploit the vulnerability of DNNs, leading to a natural urge that the strength of all attacks should be measured by both the widely used $\ell_\infty$ bound and the RMSE addressed in this paper, so that tricky enhancement of transferability would be avoided.

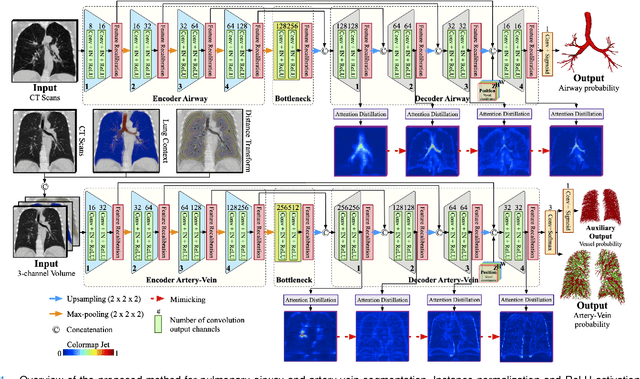
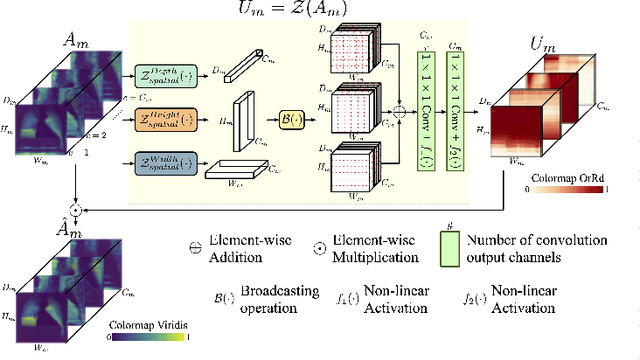
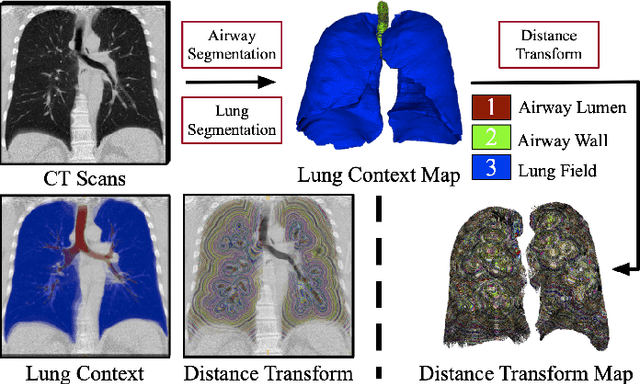
Learning Tubule-Sensitive CNNs for Pulmonary Airway and Artery-Vein Segmentation in CT

Training convolutional neural networks (CNNs) for segmentation of pulmonary airway, artery, and vein is challenging due to sparse supervisory signals caused by the severe class imbalance between tubular targets and background. We present a CNNs-based method for accurate airway and artery-vein segmentation in non-contrast computed tomography. It enjoys superior sensitivity to tenuous peripheral bronchioles, arterioles, and venules. The method first uses a feature recalibration module to make the best use of features learned from the neural networks. Spatial information of features is properly integrated to retain relative priority of activated regions, which benefits the subsequent channel-wise recalibration. Then, attention distillation module is introduced to reinforce representation learning of tubular objects. Fine-grained details in high-resolution attention maps are passing down from one layer to its previous layer recursively to enrich context. Anatomy prior of lung context map and distance transform map is designed and incorporated for better artery-vein differentiation capacity. Extensive experiments demonstrated considerable performance gains brought by these components. Compared with state-of-the-art methods, our method extracted much more branches while maintaining competitive overall segmentation performance. Codes and models will be available later at http://www.pami.sjtu.edu.cn.

Towards a Unified Quadrature Framework for Large-Scale Kernel Machines

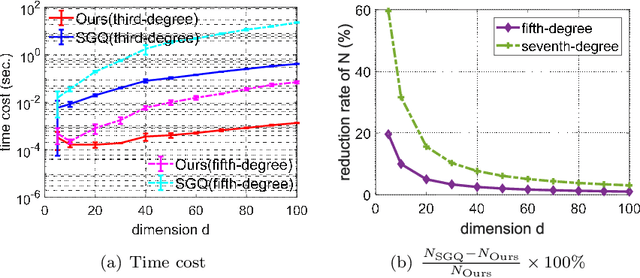
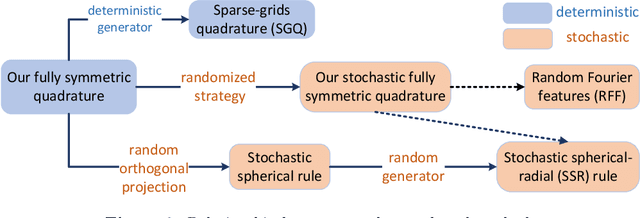
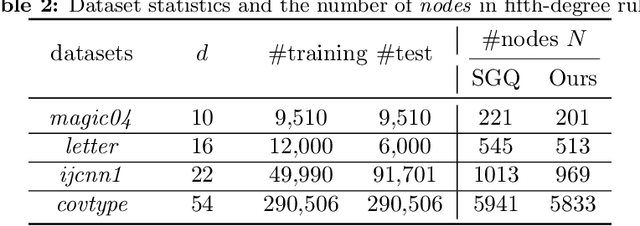
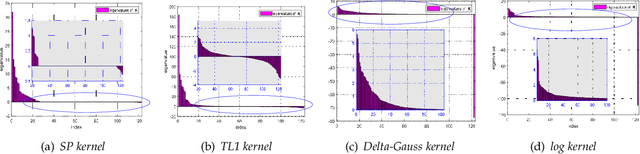
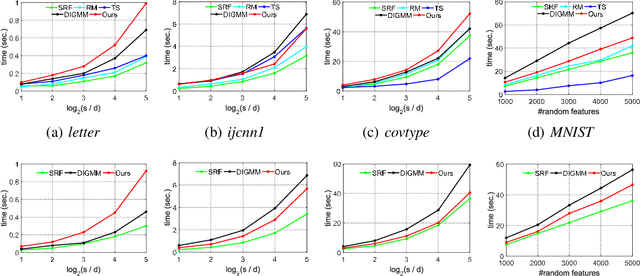
In this paper, we develop a quadrature framework for large-scale kernel machines via a numerical multiple integration representation. Leveraging the fact that the integration domain and measure of typical kernels, e.g., Gaussian kernels, arc-cosine kernels, are fully symmetric, we introduce a deterministic fully symmetric interpolatory rule to efficiently compute its quadrature nodes and associated weights to approximate such typical kernels. This interpolatory rule is able to reduce the number of needed nodes while retaining a high approximation accuracy. Further, we randomize the above deterministic rule such that the proposed stochastic version can generate dimension-adaptive feature mappings for kernel approximation. Our stochastic rule has the nice statistical properties of unbiasedness and variance reduction with fast convergence rate. In addition, we elucidate the relationship between our deterministic/stochastic interpolatory rules and current quadrature rules for kernel approximation, including the sparse grids quadrature and stochastic spherical-radial rule, thereby unifying these methods under our framework. Experimental results on several benchmark datasets show that our fully symmetric interpolatory rule compares favorably with other representative random features based methods.

Learn Robust Features via Orthogonal Multi-Path

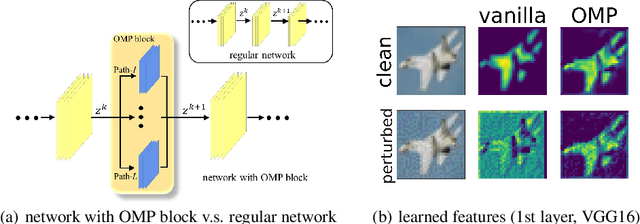
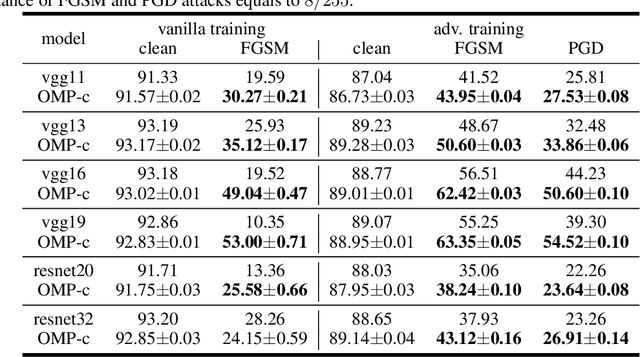
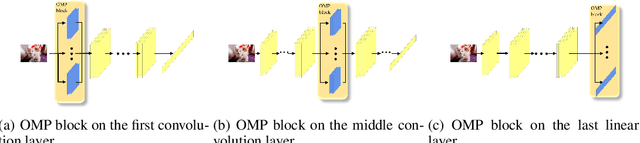
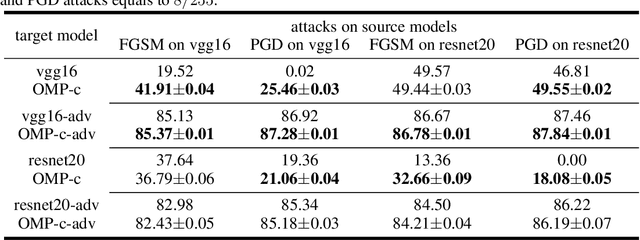
It is now widely known that by adversarial attacks, clean images with invisible perturbations can fool deep neural networks. To defend adversarial attacks, we design a block containing multiple paths to learn robust features and the parameters of these paths are required to be orthogonal with each other. The so-called Orthogonal Multi-Path (OMP) block could be posed in any layer of a neural network. Via forward learning and backward correction, one OMP block makes the neural networks learn features that are appropriate for all the paths and hence are expected to be robust. With careful design and thorough experiments on e.g., the positions of imposing orthogonality constraint, and the trade-off between the variety and accuracy, the robustness of the neural networks is significantly improved. For example, under white-box PGD attack with $l_\infty$ bound ${8}/{255}$ (this is a fierce attack that can make the accuracy of many vanilla neural networks drop to nearly $10\%$ on CIFAR10), VGG16 with the proposed OMP block could keep over $50\%$ accuracy. For black-box attacks, neural networks equipped with an OMP block have accuracy over $80\%$. The performance under both white-box and black-box attacks is much better than the existing state-of-the-art adversarial defenders.

One-shot Distributed Algorithm for Generalized Eigenvalue Problem

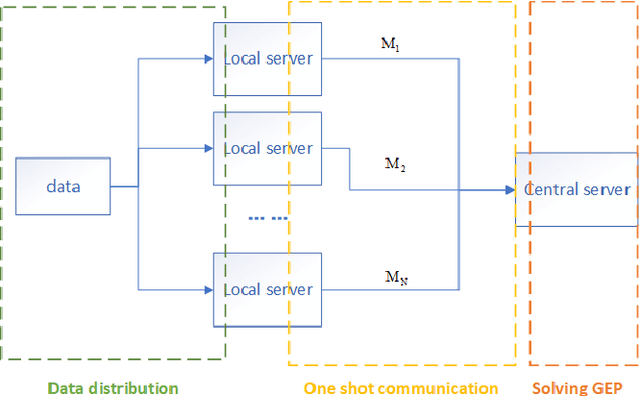
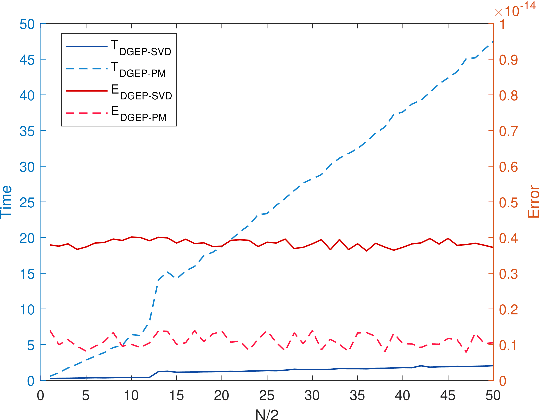
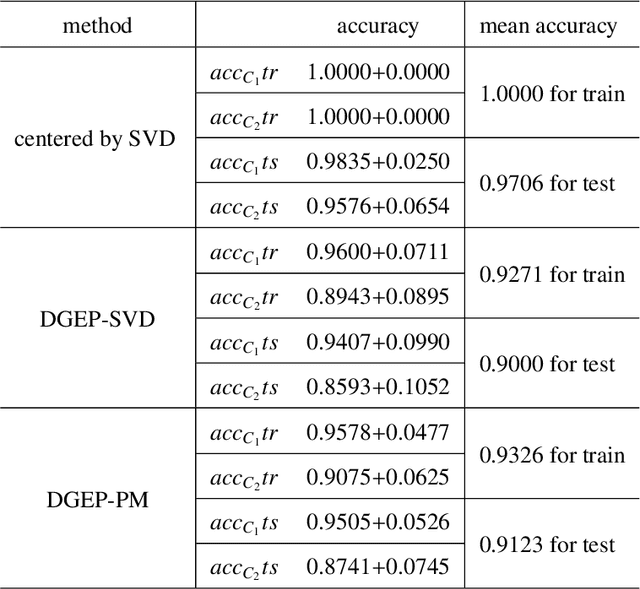
Nowadays, more and more datasets are stored in a distributed way for the sake of memory storage or data privacy. The generalized eigenvalue problem (GEP) plays a vital role in a large family of high-dimensional statistical models. However, the existing distributed method for eigenvalue decomposition cannot be applied in GEP for the divergence of the empirical covariance matrix. Here we propose a general distributed GEP framework with one-shot communication for GEP. If the symmetric data covariance has repeated eigenvalues, e.g., in canonical component analysis, we further modify the method for better convergence. The theoretical analysis on approximation error is conducted and the relation to the divergence of the data covariance, the eigenvalues of the empirical data covariance, and the number of local servers is analyzed. Numerical experiments also show the effectiveness of the proposed algorithms.

End-to-end Kernel Learning via Generative Random Fourier Features

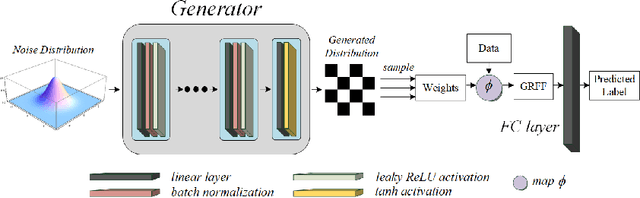
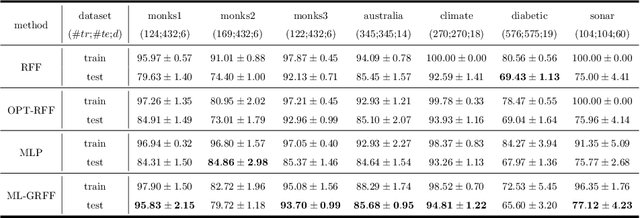
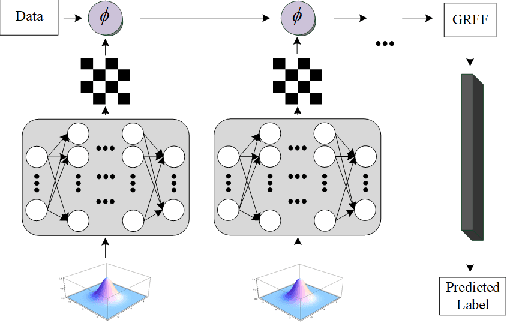
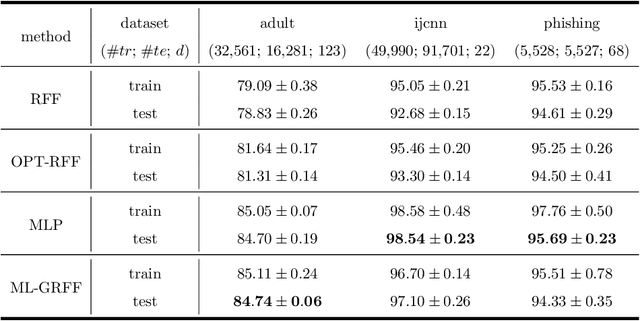
Random Fourier features enable researchers to build feature map to learn the spectral distribution of the underlying kernel. Current distribution-based methods follow a two-stage scheme: they first learn and optimize the feature map by solving the kernel alignment problem, then learn a linear classifier on the features. However, since the ideal kernel in kernel alignment problem is not necessarily optimal in classification tasks, the generalization performance of the random features learned in this two-stage manner can perhaps be further improved. To address this issue, we propose an end-to-end, one-stage kernel learning approach, called generative random Fourier features, which jointly learns the features and the classifier. A generative network is involved to implicitly learn and to sample from the distribution of the latent kernel. Random features are then built via the generative weights and followed by a linear classifier parameterized as a full-connected layer. We jointly train the generative network and the classifier by solving the empirical risk minimization problem for a one-stage solution. Straightly minimizing the loss between predictive and true labels brings better generalization performance. Besides, this end-to-end strategy allows us to increase the depth of features, resulting in multi-layer architecture and exhibiting strong linear-separable pattern. Empirical results demonstrate the superiority of our method in classification tasks over other two-stage kernel learning methods. Finally, we investigate the robustness of proposed method in defending adversarial attacks, which shows that the randomization and resampling mechanism associated with the learned distribution can alleviate the performance decrease brought by adversarial examples.

Attack on Multi-Node Attention for Object Detection

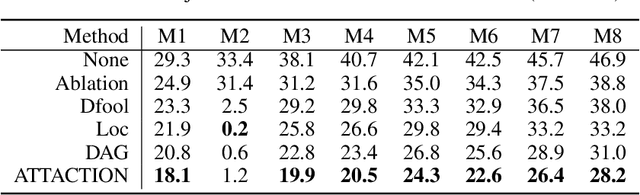
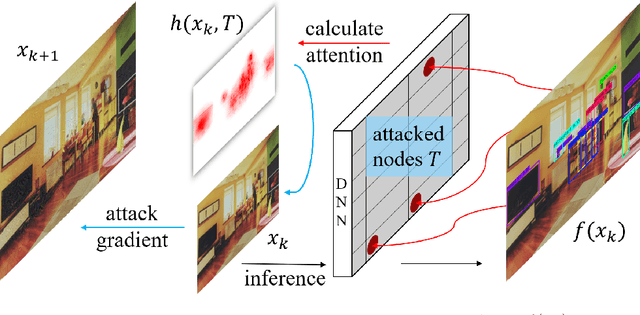
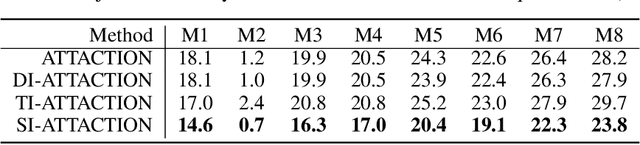
This paper focuses on high-transferable adversarial attacks on detection networks, which are crucial for life-concerning systems such as autonomous driving and security surveillance. Detection networks are hard to attack in a black-box manner, because of their multiple-output property and diversity across architectures. To pursue a high attacking transferability, one needs to find a common property shared by different models. Multi-node attention heat map obtained by our newly proposed method is such a property. Based on it, we design the ATTACk on multi-node attenTION for object detecTION (ATTACTION). ATTACTION achieves a state-of-the-art transferability in numerical experiments. On MS COCO, the detection mAP for all 7 tested black-box architectures is halved and the performance of semantic segmentation is greatly influenced. Given the great transferability of ATTACTION, we generate Adversarial Objects in COntext (AOCO), the first adversarial dataset on object detection networks, which could help designers to quickly evaluate and improve the robustness of detection networks.

Analysis of Least Squares Regularized Regression in Reproducing Kernel Krein Spaces

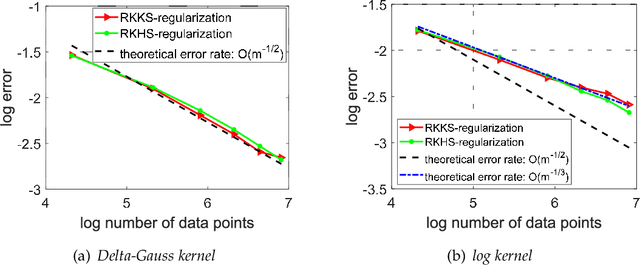
In this paper, we study the asymptotical properties of least squares regularized regression with indefinite kernels in reproducing kernel Kre\u{\i}n spaces (RKKS). The classical approximation analysis cannot be directly applied to study its asymptotical behavior under the framework of learning theory as this problem is in essence non-convex and outputs stationary points. By introducing a bounded hyper-sphere constraint to such non-convex regularized risk minimization problem, we theoretically demonstrate that this problem has a globally optimal solution with a closed form on the sphere, which makes our approximation analysis feasible in RKKS. Accordingly, we modify traditional error decomposition techniques, prove convergence results for the introduced hypothesis error based on matrix perturbation theory, and derive learning rates of such regularized regression problem in RKKS. Under some conditions, the derived learning rates in RKKS are the same as that in reproducing kernel Hilbert spaces (RKHS), which is actually the first work on approximation analysis of regularized learning algorithms in RKKS.

Generalizing Random Fourier Features via Generalized Measures

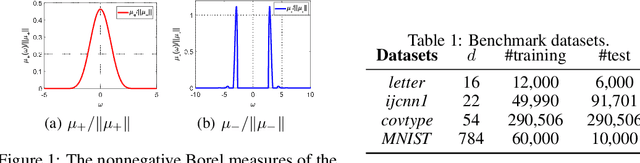
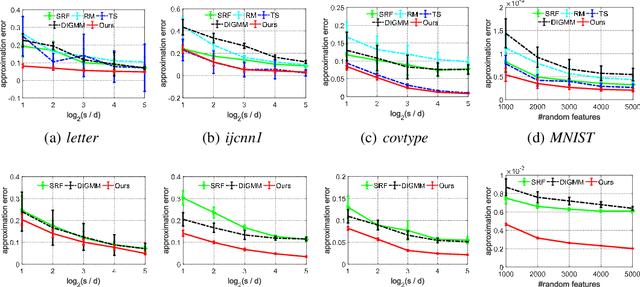
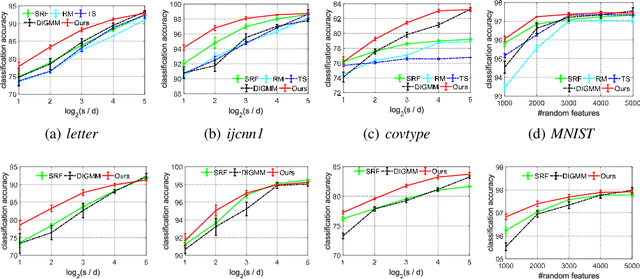
We generalize random Fourier features, that usually require kernel functions to be both stationary and positive definite (PD), to a more general range of non-stationary or/and non-PD kernels, e.g., dot-product kernels on the unit sphere and a linear combination of positive definite kernels. Specifically, we find that the popular neural tangent kernel in two-layer ReLU network, a typical dot-product kernel, is shift-invariant but not positive definite if we consider $\ell_2$-normalized data. By introducing the signed measure, we propose a general framework that covers the above kernels by associating them with specific finite Borel measures, i.e., probability distributions. In this manner, we are able to provide the first random features algorithm to obtain unbiased estimation of these kernels. Experiments on several benchmark datasets verify the effectiveness of our algorithm over the existing methods. Last but not least, our work provides a sufficient and necessary condition, which is also computationally implementable, to solve a long-lasting open question: does any indefinite kernel have a positive decomposition?

A Communication-Efficient Distributed Algorithm for Kernel Principal Component Analysis

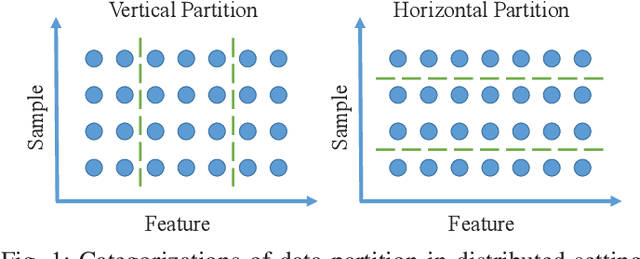
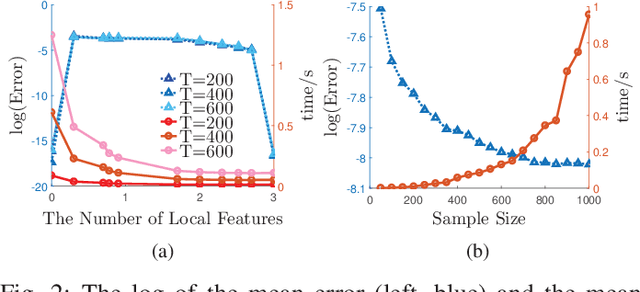
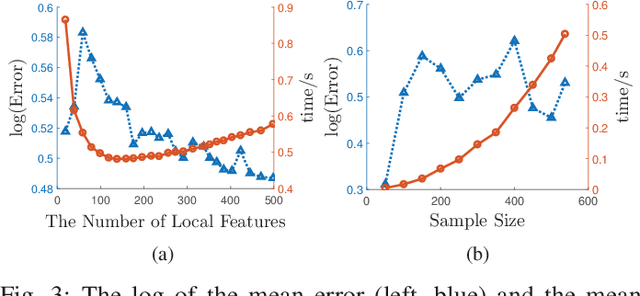
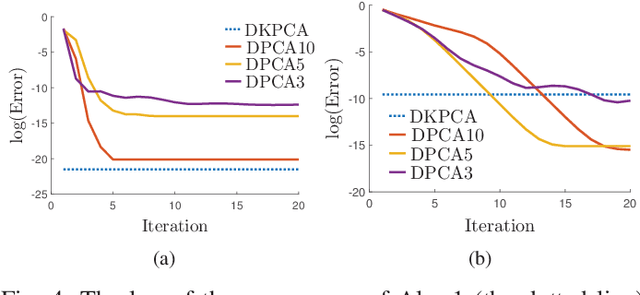
Principal Component Analysis (PCA) is a fundamental technology in machine learning. Nowadays many high-dimension large datasets are acquired in a distributed manner, which precludes the use of centralized PCA due to the high communication cost and privacy risk. Thus, many distributed PCA algorithms are proposed, most of which, however, focus on linear cases. To efficiently extract non-linear features, this brief proposes a communication-efficient distributed kernel PCA algorithm, where linear and RBF kernels are applied. The key is to estimate the global empirical kernel matrix from the eigenvectors of local kernel matrices. The approximate error of the estimators is theoretically analyzed for both linear and RBF kernels. The result suggests that when eigenvalues decay fast, which is common for RBF kernels, the proposed algorithm gives high quality results with low communication cost. Results of simulation experiments verify our theory analysis and experiments on GSE2187 dataset show the effectiveness of the proposed algorithm.