Gated Group Self-Attention for Answer Selection

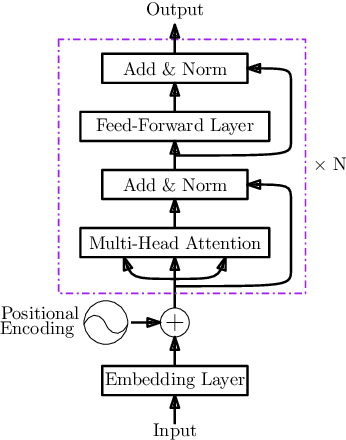
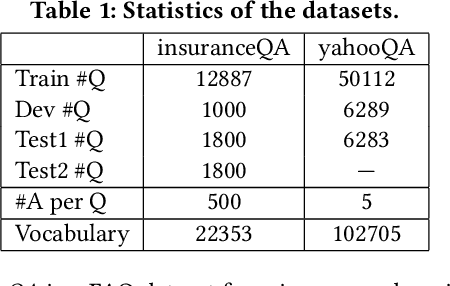
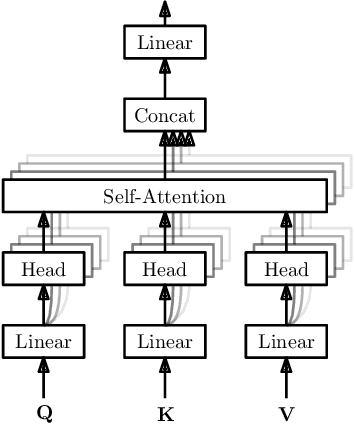
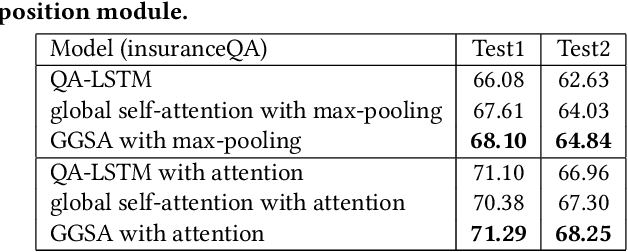
Answer selection (answer ranking) is one of the key steps in many kinds of question answering (QA) applications, where deep models have achieved state-of-the-art performance. Among these deep models, recurrent neural network (RNN) based models are most popular, typically with better performance than convolutional neural network (CNN) based models. Nevertheless, it is difficult for RNN based models to capture the information about long-range dependency among words in the sentences of questions and answers. In this paper, we propose a new deep model, called gated group self-attention (GGSA), for answer selection. GGSA is inspired by global self-attention which is originally proposed for machine translation and has not been explored in answer selection. GGSA tackles the problem of global self-attention that local and global information cannot be well distinguished. Furthermore, an interaction mechanism between questions and answers is also proposed to enhance GGSA by a residual structure. Experimental results on two popular QA datasets show that GGSA can outperform existing answer selection models to achieve state-of-the-art performance. Furthermore, GGSA can also achieve higher accuracy than global self-attention for the answer selection task, with a lower computation cost.

Hashing based Answer Selection

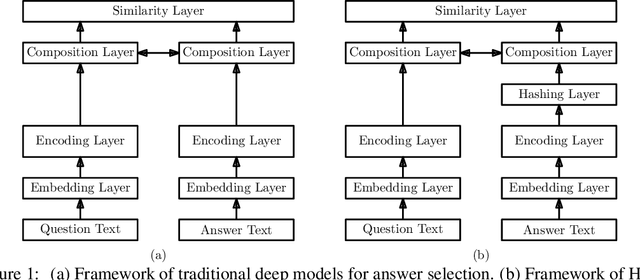
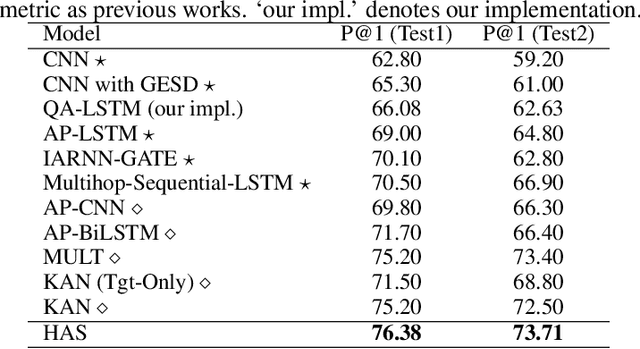
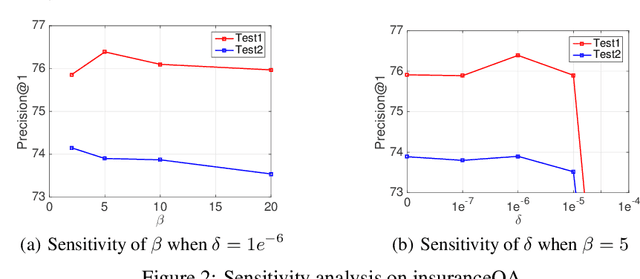
Answer selection is an important subtask of question answering (QA), where deep models usually achieve better performance. Most deep models adopt question-answer interaction mechanisms, such as attention, to get vector representations for answers. When these interaction based deep models are deployed for online prediction, the representations of all answers need to be recalculated for each question. This procedure is time-consuming for deep models with complex encoders like BERT which usually have better accuracy than simple encoders. One possible solution is to store the matrix representation (encoder output) of each answer in memory to avoid recalculation. But this will bring large memory cost. In this paper, we propose a novel method, called hashing based answer selection (HAS), to tackle this problem. HAS adopts a hashing strategy to learn a binary matrix representation for each answer, which can dramatically reduce the memory cost for storing the matrix representations of answers. Hence, HAS can adopt complex encoders like BERT in the model, but the online prediction of HAS is still fast with a low memory cost. Experimental results on three popular answer selection datasets show that HAS can outperform existing models to achieve state-of-the-art performance.

Quantized Epoch-SGD for Communication-Efficient Distributed Learning

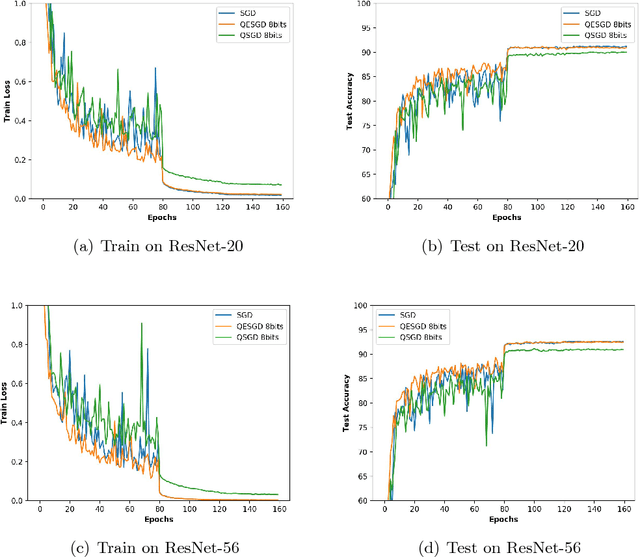
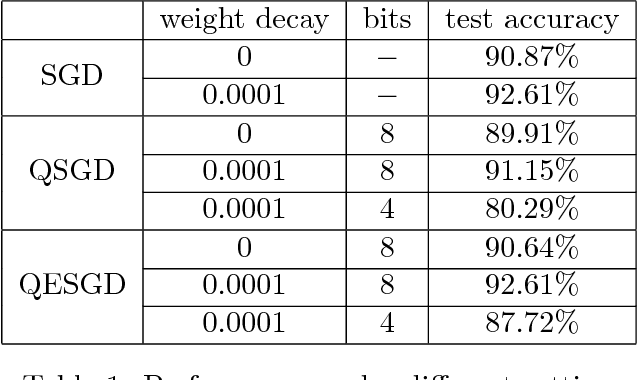
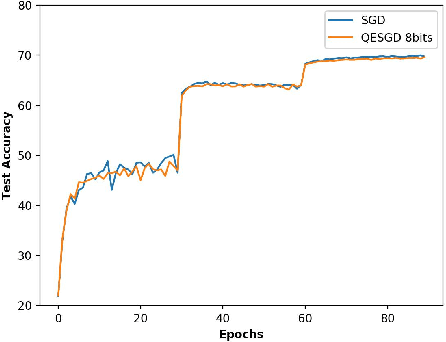
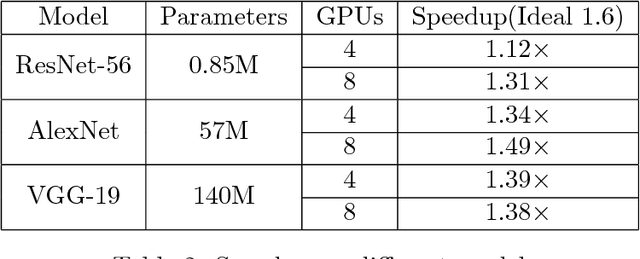
Due to its efficiency and ease to implement, stochastic gradient descent (SGD) has been widely used in machine learning. In particular, SGD is one of the most popular optimization methods for distributed learning. Recently, quantized SGD (QSGD), which adopts quantization to reduce the communication cost in SGD-based distributed learning, has attracted much attention. Although several QSGD methods have been proposed, some of them are heuristic without theoretical guarantee, and others have high quantization variance which makes the convergence become slow. In this paper, we propose a new method, called Quantized Epoch-SGD (QESGD), for communication-efficient distributed learning. QESGD compresses (quantizes) the parameter with variance reduction, so that it can get almost the same performance as that of SGD with less communication cost. QESGD is implemented on the Parameter Server framework, and empirical results on distributed deep learning show that QESGD can outperform other state-of-the-art quantization methods to achieve the best performance.

Proximal SCOPE for Distributed Sparse Learning: Better Data Partition Implies Faster Convergence Rate

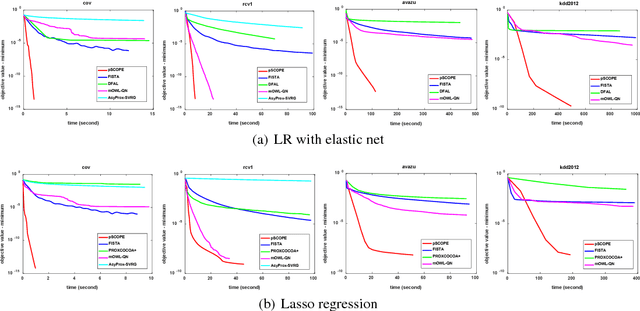
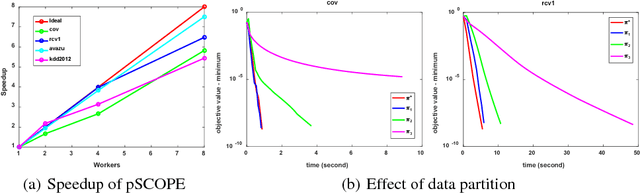
Distributed sparse learning with a cluster of multiple machines has attracted much attention in machine learning, especially for large-scale applications with high-dimensional data. One popular way to implement sparse learning is to use $L_1$ regularization. In this paper, we propose a novel method, called proximal \mbox{SCOPE}~(\mbox{pSCOPE}), for distributed sparse learning with $L_1$ regularization. pSCOPE is based on a \underline{c}ooperative \underline{a}utonomous \underline{l}ocal \underline{l}earning~(\mbox{CALL}) framework. In the \mbox{CALL} framework of \mbox{pSCOPE}, we find that the data partition affects the convergence of the learning procedure, and subsequently we define a metric to measure the goodness of a data partition. Based on the defined metric, we theoretically prove that pSCOPE is convergent with a linear convergence rate if the data partition is good enough. We also prove that better data partition implies faster convergence rate. Furthermore, pSCOPE is also communication efficient. Experimental results on real data sets show that pSCOPE can outperform other state-of-the-art distributed methods for sparse learning.

Convolutional Geometric Matrix Completion

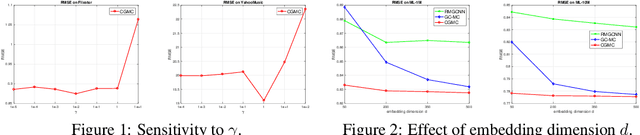
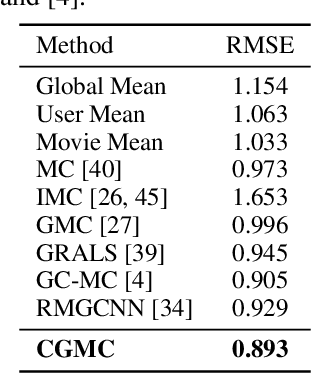
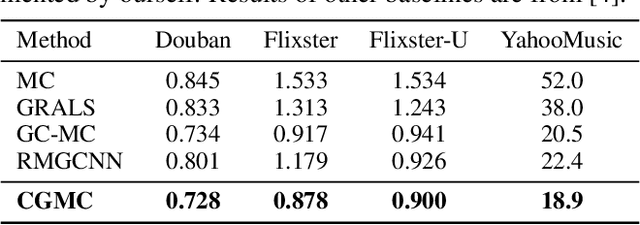
Geometric matrix completion~(GMC) has been proposed for recommendation by integrating the relationship~(link) graphs among users/items into matrix completion~(MC) . Traditional \mbox{GMC} methods typically adopt graph regularization to impose smoothness priors for \mbox{MC}. Recently, geometric deep learning on graphs~(\mbox{GDLG}) is proposed to solve the GMC problem, showing better performance than existing GMC methods including traditional graph regularization based methods. To the best of our knowledge, there exists only one GDLG method for GMC, which is called \mbox{RMGCNN}. RMGCNN combines graph convolutional network~(GCN) and recurrent neural network~(RNN) together for GMC. In the original work of RMGCNN, RMGCNN demonstrates better performance than pure GCN-based method. In this paper, we propose a new \mbox{GMC} method, called \underline{c}onvolutional \underline{g}eometric \underline{m}atrix \underline{c}ompletion~(CGMC), for recommendation with graphs among users/items. CGMC is a pure GCN-based method with a newly designed graph convolutional network. Experimental results on real datasets show that CGMC can outperform other state-of-the-art methods including RMGCNN.

Feature-Distributed SVRG for High-Dimensional Linear Classification

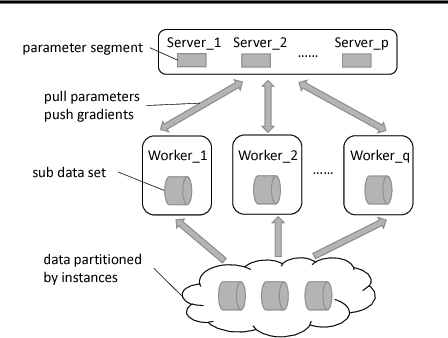
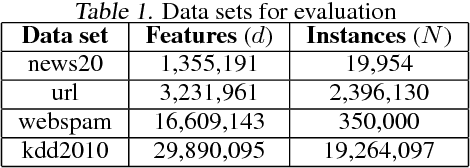
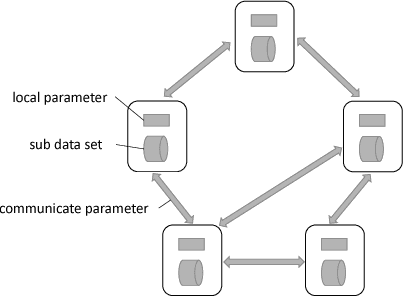
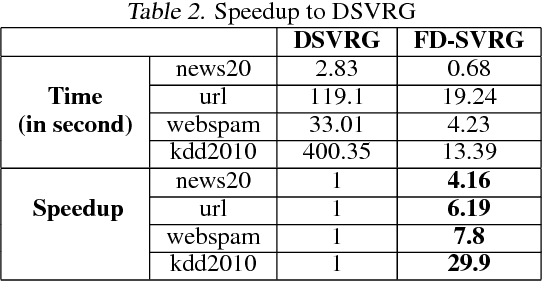
Linear classification has been widely used in many high-dimensional applications like text classification. To perform linear classification for large-scale tasks, we often need to design distributed learning methods on a cluster of multiple machines. In this paper, we propose a new distributed learning method, called feature-distributed stochastic variance reduced gradient (FD-SVRG) for high-dimensional linear classification. Unlike most existing distributed learning methods which are instance-distributed, FD-SVRG is feature-distributed. FD-SVRG has lower communication cost than other instance-distributed methods when the data dimensionality is larger than the number of data instances. Experimental results on real data demonstrate that FD-SVRG can outperform other state-of-the-art distributed methods for high-dimensional linear classification in terms of both communication cost and wall-clock time, when the dimensionality is larger than the number of instances in training data.

Robust Frequent Directions with Application in Online Learning

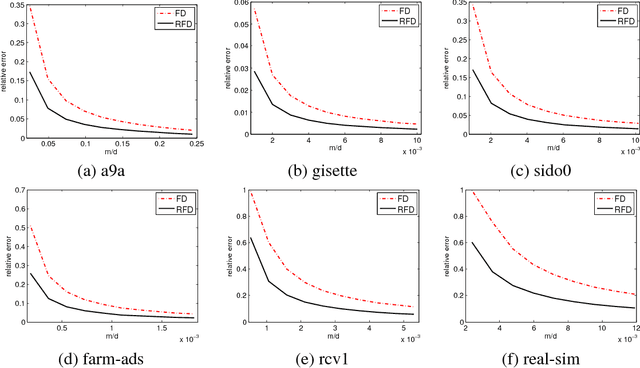
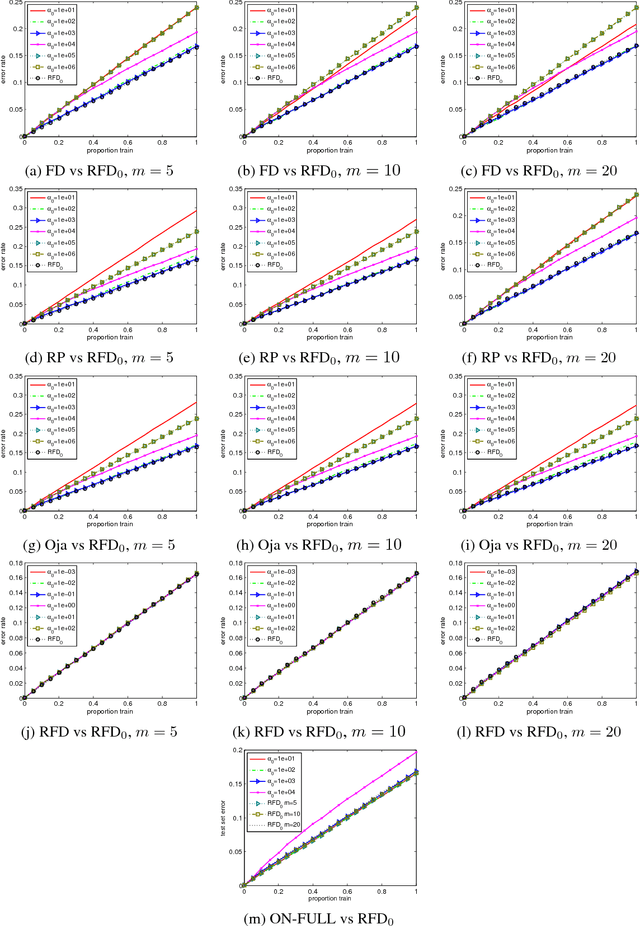
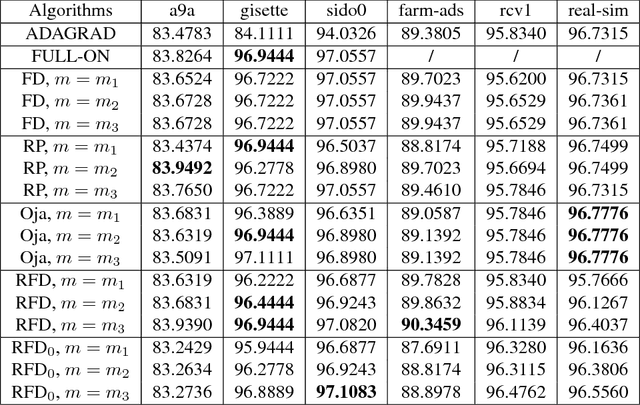
The frequent directions (FD) technique is a deterministic approach for online sketching that has many applications in machine learning. The conventional FD is a heuristic procedure that often generates rank deficient matrices. To overcome the rank deficiency problem, we propose a new sketching strategy called robust frequent directions (RFD) by introducing a regularization term. RFD can be derived from an optimization problem. It updates the sketch matrix and the regularization term adaptively and jointly. RFD reduces the approximation error of FD without changing the computational cost. We also apply RFD to online learning and propose an effective hyperparameter-free online Newton algorithm. We derive a regret bound for our online Newton algorithm based on RFD, which guarantees the robustness of the algorithm. The experimental studies demonstrate that the proposed method outperforms sate-of-the-art second order online learning algorithms.

Asymmetric Deep Supervised Hashing

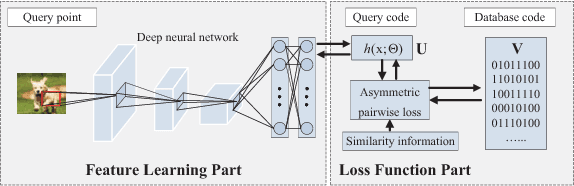
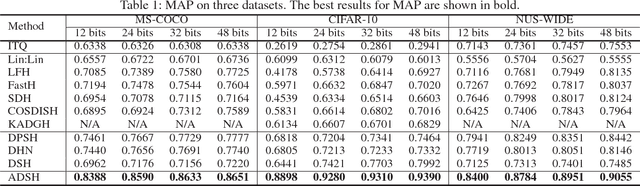
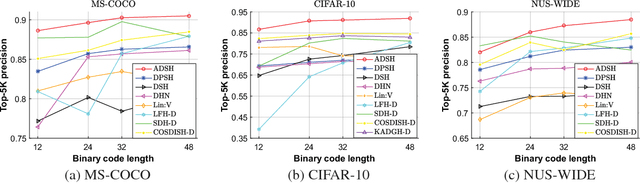
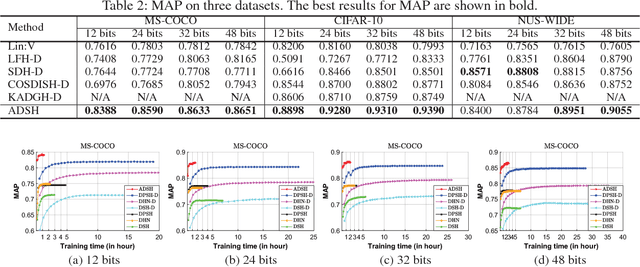
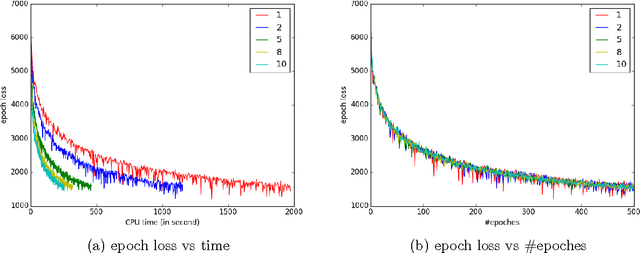
Hashing has been widely used for large-scale approximate nearest neighbor search because of its storage and search efficiency. Recent work has found that deep supervised hashing can significantly outperform non-deep supervised hashing in many applications. However, most existing deep supervised hashing methods adopt a symmetric strategy to learn one deep hash function for both query points and database (retrieval) points. The training of these symmetric deep supervised hashing methods is typically time-consuming, which makes them hard to effectively utilize the supervised information for cases with large-scale database. In this paper, we propose a novel deep supervised hashing method, called asymmetric deep supervised hashing (ADSH), for large-scale nearest neighbor search. ADSH treats the query points and database points in an asymmetric way. More specifically, ADSH learns a deep hash function only for query points, while the hash codes for database points are directly learned. The training of ADSH is much more efficient than that of traditional symmetric deep supervised hashing methods. Experiments show that ADSH can achieve state-of-the-art performance in real applications.

ParaGraphE: A Library for Parallel Knowledge Graph Embedding

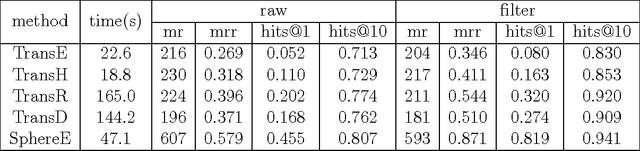
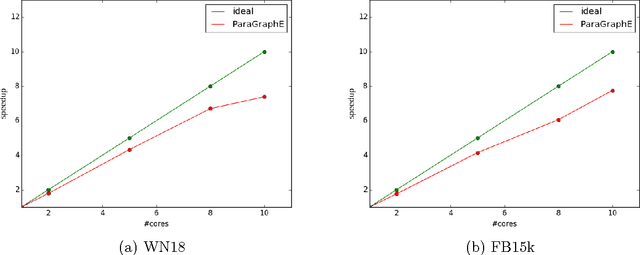
Knowledge graph embedding aims at translating the knowledge graph into numerical representations by transforming the entities and relations into continuous low-dimensional vectors. Recently, many methods [1, 5, 3, 2, 6] have been proposed to deal with this problem, but existing single-thread implementations of them are time-consuming for large-scale knowledge graphs. Here, we design a unified parallel framework to parallelize these methods, which achieves a significant time reduction without influencing the accuracy. We name our framework as ParaGraphE, which provides a library for parallel knowledge graph embedding. The source code can be downloaded from https://github.com/LIBBLE/LIBBLE-MultiThread/tree/master/ParaGraphE .

Lock-Free Optimization for Non-Convex Problems

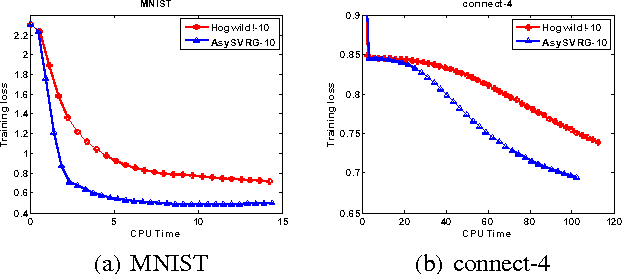
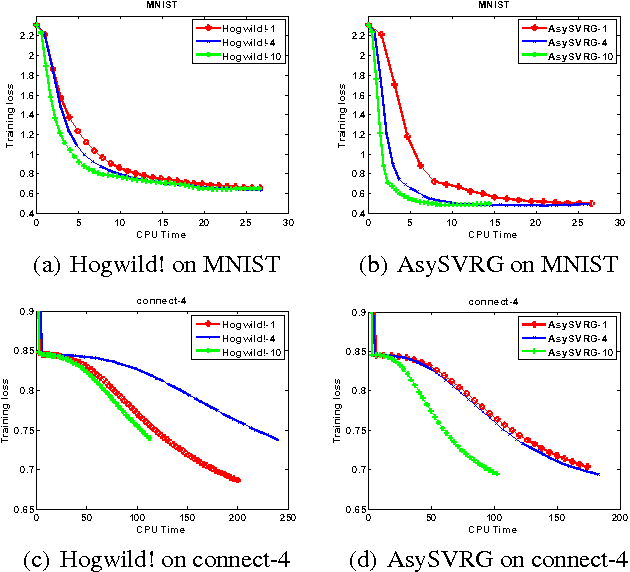
Stochastic gradient descent~(SGD) and its variants have attracted much attention in machine learning due to their efficiency and effectiveness for optimization. To handle large-scale problems, researchers have recently proposed several lock-free strategy based parallel SGD~(LF-PSGD) methods for multi-core systems. However, existing works have only proved the convergence of these LF-PSGD methods for convex problems. To the best of our knowledge, no work has proved the convergence of the LF-PSGD methods for non-convex problems. In this paper, we provide the theoretical proof about the convergence of two representative LF-PSGD methods, Hogwild! and AsySVRG, for non-convex problems. Empirical results also show that both Hogwild! and AsySVRG are convergent on non-convex problems, which successfully verifies our theoretical results.