Parallel and Proximal Linear-Quadratic Methods for Real-Time Constrained Model-Predictive Control

-Recent strides in model predictive control (MPC)underscore a dependence on numerical advancements to efficientlyand accurately solve large-scale problems. Given the substantialnumber of variables characterizing typical whole-body optimalcontrol (OC) problems -often numbering in the thousands-exploiting the sparse structure of the numerical problem becomescrucial to meet computational demands, typically in the range ofa few milliseconds. A fundamental building block for computingNewton or Sequential Quadratic Programming (SQP) steps indirect optimal control methods involves addressing the linearquadratic regulator (LQR) problem. This paper concentrateson equality-constrained problems featuring implicit systemdynamics and dual regularization, a characteristic found inadvanced interior-point or augmented Lagrangian solvers. Here,we introduce a parallel algorithm designed for solving an LQRproblem with dual regularization. Leveraging a rewriting of theLQR recursion through block elimination, we first enhanced theefficiency of the serial algorithm, then subsequently generalized itto handle parametric problems. This extension enables us to splitdecision variables and solve multiple subproblems concurrently.Our algorithm is implemented in our nonlinear numerical optimalcontrol library ALIGATOR. It showcases improved performanceover previous serial formulations and we validate its efficacy bydeploying it in the model predictive control of a real quadrupedrobot. This paper follows up from our prior work on augmentedLagrangian methods for numerical optimal control with implicitdynamics and constraints.

Contact Models in Robotics: a Comparative Analysis

Physics simulation is ubiquitous in robotics. Whether in model-based approaches (e.g., trajectory optimization), or model-free algorithms (e.g., reinforcement learning), physics simulators are a central component of modern control pipelines in robotics. Over the past decades, several robotic simulators have been developed, each with dedicated contact modeling assumptions and algorithmic solutions. In this article, we survey the main contact models and the associated numerical methods commonly used in robotics for simulating advanced robot motions involving contact interactions. In particular, we recall the physical laws underlying contacts and friction (i.e., Signorini condition, Coulomb's law, and the maximum dissipation principle), and how they are transcribed in current simulators. For each physics engine, we expose their inherent physical relaxations along with their limitations due to the numerical techniques employed. Based on our study, we propose theoretically grounded quantitative criteria on which we build benchmarks assessing both the physical and computational aspects of simulation. We support our work with an open-source and efficient C++ implementation of the existing algorithmic variations. Our results demonstrate that some approximations or algorithms commonly used in robotics can severely widen the reality gap and impact target applications. We hope this work will help motivate the development of new contact models, contact solvers, and robotic simulators in general, at the root of recent progress in motion generation in robotics.

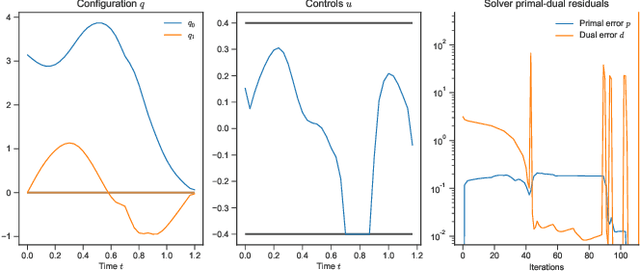
Constrained Differential Dynamic Programming: A primal-dual augmented Lagrangian approach

Trajectory optimization is an efficient approach for solving optimal control problems for complex robotic systems. It relies on two key components: first the transcription into a sparse nonlinear program, and second the corresponding solver to iteratively compute its solution. On one hand, differential dynamic programming (DDP) provides an efficient approach to transcribe the optimal control problem into a finite-dimensional problem while optimally exploiting the sparsity induced by time. On the other hand, augmented Lagrangian methods make it possible to formulate efficient algorithms with advanced constraint-satisfaction strategies. In this paper, we propose to combine these two approaches into an efficient optimal control algorithm accepting both equality and inequality constraints. Based on the augmented Lagrangian literature, we first derive a generic primal-dual augmented Lagrangian strategy for nonlinear problems with equality and inequality constraints. We then apply it to the dynamic programming principle to solve the value-greedy optimization problems inherent to the backward pass of DDP, which we combine with a dedicated globalization strategy, resulting in a Newton-like algorithm for solving constrained trajectory optimization problems. Contrary to previous attempts of formulating an augmented Lagrangian version of DDP, our approach exhibits adequate convergence properties without any switch in strategies. We empirically demonstrate its interest with several case-studies from the robotics literature.

ProxNLP: a primal-dual augmented Lagrangian solver for nonlinear programming in Robotics and beyond

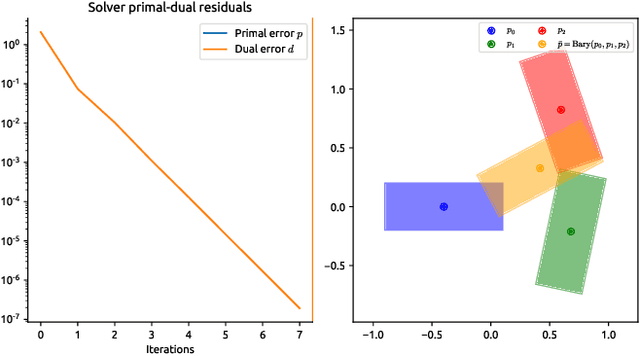
Mathematical optimization is the workhorse behind several aspects of modern robotics and control. In these applications, the focus is on constrained optimization, and the ability to work on manifolds (such as the classical matrix Lie groups), along with a specific requirement for robustness and speed. In recent years, augmented Lagrangian methods have seen a resurgence due to their robustness and flexibility, their connections to (inexact) proximal-point methods, and their interoperability with Newton or semismooth Newton methods. In the sequel, we present primal-dual augmented Lagrangian method for inequality-constrained problems on manifolds, which we introduced in our recent work, as well as an efficient C++ implementation suitable for use in robotics applications and beyond.

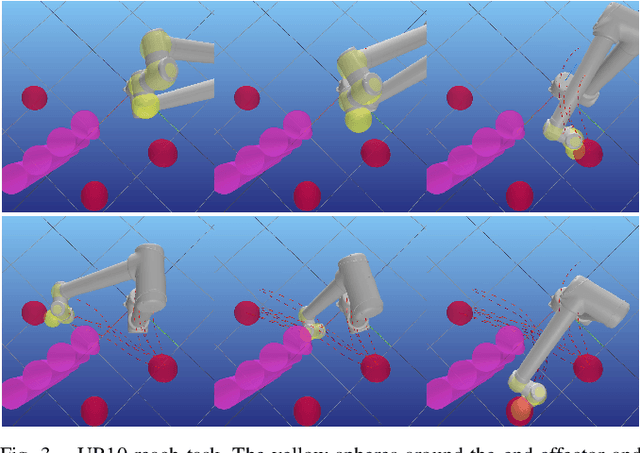
Enforcing the consensus between Trajectory Optimization and Policy Learning for precise robot control

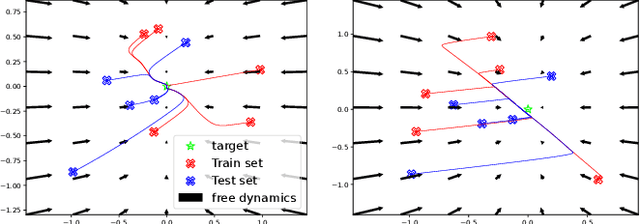
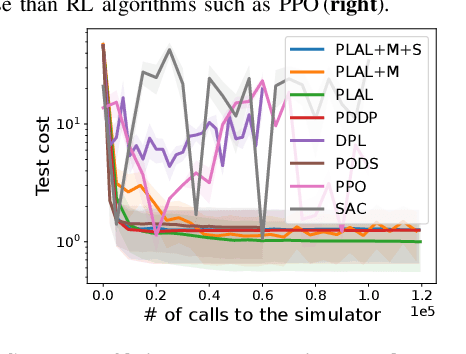
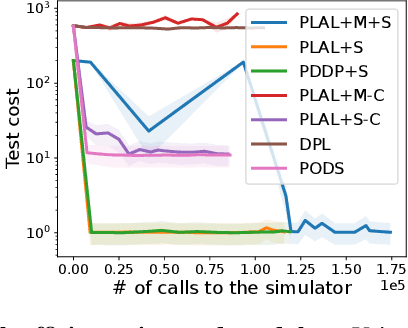
Reinforcement learning (RL) and trajectory optimization (TO) present strong complementary advantages. On one hand, RL approaches are able to learn global control policies directly from data, but generally require large sample sizes to properly converge towards feasible policies. On the other hand, TO methods are able to exploit gradient-based information extracted from simulators to quickly converge towards a locally optimal control trajectory which is only valid within the vicinity of the solution. Over the past decade, several approaches have aimed to adequately combine the two classes of methods in order to obtain the best of both worlds. Following on from this line of research, we propose several improvements on top of these approaches to learn global control policies quicker, notably by leveraging sensitivity information stemming from TO methods via Sobolev learning, and augmented Lagrangian techniques to enforce the consensus between TO and policy learning. We evaluate the benefits of these improvements on various classical tasks in robotics through comparison with existing approaches in the literature.