A Differentiable Programming System to Bridge Machine Learning and Scientific Computing

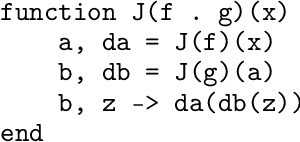
Scientific computing is increasingly incorporating the advancements in machine learning and the ability to work with large amounts of data. At the same time, machine learning models are becoming increasingly sophisticated and exhibit many features often seen in scientific computing, stressing the capabilities of machine learning frameworks. Just as the disciplines of scientific computing and machine learning have shared common underlying infrastructure in the form of numerical linear algebra, we now have the opportunity to further share new computational infrastructure, and thus ideas, in the form of Differentiable Programming. We describe Zygote, a Differentiable Programming system that is able to take gradients of general program structures. We implement this system in the Julia programming language. Our system supports almost all language constructs (control flow, recursion, mutation, etc.) and compiles high-performance code without requiring any user intervention or refactoring to stage computations. This enables an expressive programming model for deep learning, but more importantly, it enables us to incorporate a large ecosystem of libraries in our models in a straightforward way. We discuss our approach to automatic differentiation, including its support for advanced techniques such as mixed-mode, complex and checkpointed differentiation, and present several examples of differentiating programs.

DiffEqFlux.jl - A Julia Library for Neural Differential Equations

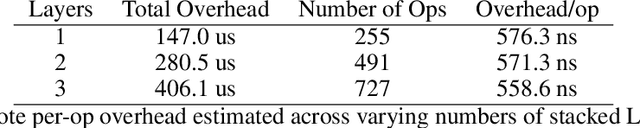
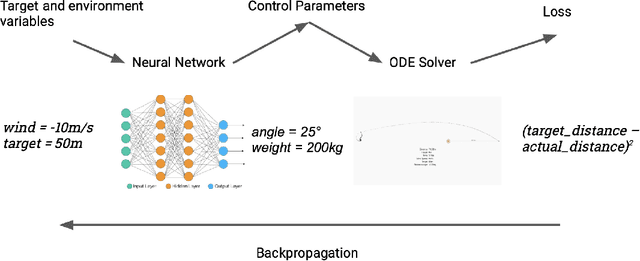
DiffEqFlux.jl is a library for fusing neural networks and differential equations. In this work we describe differential equations from the viewpoint of data science and discuss the complementary nature between machine learning models and differential equations. We demonstrate the ability to incorporate DifferentialEquations.jl-defined differential equation problems into a Flux-defined neural network, and vice versa. The advantages of being able to use the entire DifferentialEquations.jl suite for this purpose is demonstrated by counter examples where simple integration strategies fail, but the sophisticated integration strategies provided by the DifferentialEquations.jl library succeed. This is followed by a demonstration of delay differential equations and stochastic differential equations inside of neural networks. We show high-level functionality for defining neural ordinary differential equations (neural networks embedded into the differential equation) and describe the extra models in the Flux model zoo which includes neural stochastic differential equations. We conclude by discussing the various adjoint methods used for backpropogation of the differential equation solvers. DiffEqFlux.jl is an important contribution to the area, as it allows the full weight of the differential equation solvers developed from decades of research in the scientific computing field to be readily applied to the challenges posed by machine learning and data science.