Elign: Equivariant Diffusion Model Alignment from Foundational Machine Learning Force Fields

Generative models for 3D molecular conformations must respect Euclidean symmetries and concentrate probability mass on thermodynamically favorable, mechanically stable structures. However, E(3)-equivariant diffusion models often reproduce biases from semi-empirical training data rather than capturing the equilibrium distribution of a high-fidelity Hamiltonian. While physics-based guidance can correct this, it faces two computational bottlenecks: expensive quantum-chemical evaluations (e.g., DFT) and the need to repeat such queries at every sampling step. We present Elign, a post-training framework that amortizes both costs. First, we replace expensive DFT evaluations with a faster, pretrained foundational machine-learning force field (MLFF) to provide physical signals. Second, we eliminate repeated run-time queries by shifting physical steering to the training phase. To achieve the second amortization, we formulate reverse diffusion as a reinforcement learning problem and introduce Force--Energy Disentangled Group Relative Policy Optimization (FED-GRPO) to fine-tune the denoising policy. FED-GRPO includes a potential-based energy reward and a force-based stability reward, which are optimized and group-normalized independently. Experiments show that Elign generates conformations with lower gold-standard DFT energies and forces, while improving stability. Crucially, inference remains as fast as unguided sampling, since no energy evaluations are required during generation.

Machine Number Sense: A Dataset of Visual Arithmetic Problems for Abstract and Relational Reasoning

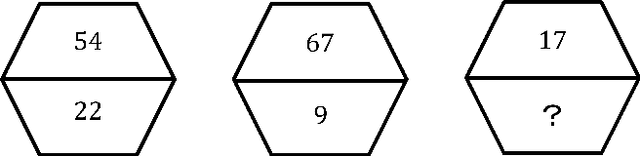
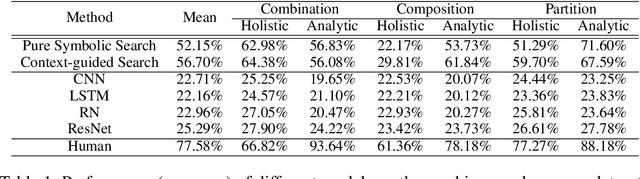
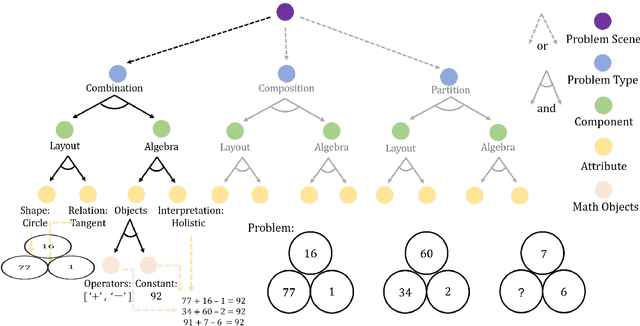
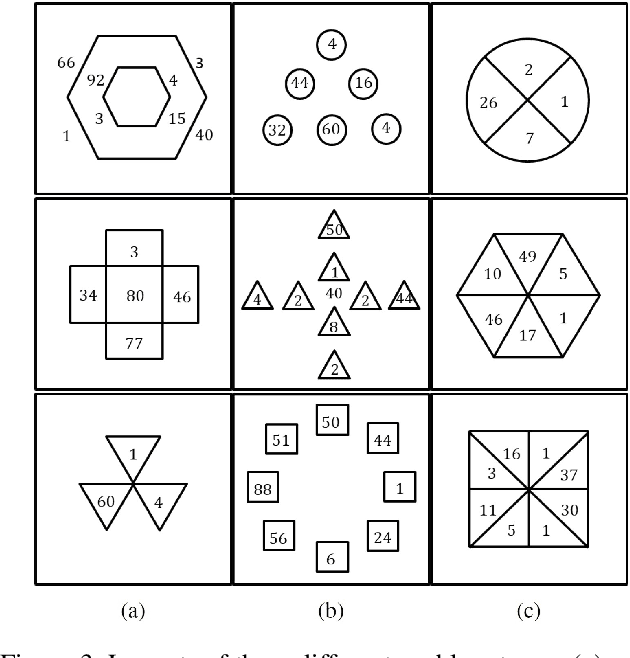
As a comprehensive indicator of mathematical thinking and intelligence, the number sense (Dehaene 2011) bridges the induction of symbolic concepts and the competence of problem-solving. To endow such a crucial cognitive ability to machine intelligence, we propose a dataset, Machine Number Sense (MNS), consisting of visual arithmetic problems automatically generated using a grammar model--And-Or Graph (AOG). These visual arithmetic problems are in the form of geometric figures: each problem has a set of geometric shapes as its context and embedded number symbols. Solving such problems is not trivial; the machine not only has to recognize the number, but also to interpret the number with its contexts, shapes, and relations (e.g., symmetry) together with proper operations. We benchmark the MNS dataset using four predominant neural network models as baselines in this visual reasoning task. Comprehensive experiments show that current neural-network-based models still struggle to understand number concepts and relational operations. We show that a simple brute-force search algorithm could work out some of the problems without context information. Crucially, taking geometric context into account by an additional perception module would provide a sharp performance gain with fewer search steps. Altogether, we call for attention in fusing the classic search-based algorithms with modern neural networks to discover the essential number concepts in future research.