Nonparametric Teaching for Graph Property Learners

Inferring properties of graph-structured data, e.g., the solubility of molecules, essentially involves learning the implicit mapping from graphs to their properties. This learning process is often costly for graph property learners like Graph Convolutional Networks (GCNs). To address this, we propose a paradigm called Graph Neural Teaching (GraNT) that reinterprets the learning process through a novel nonparametric teaching perspective. Specifically, the latter offers a theoretical framework for teaching implicitly defined (i.e., nonparametric) mappings via example selection. Such an implicit mapping is realized by a dense set of graph-property pairs, with the GraNT teacher selecting a subset of them to promote faster convergence in GCN training. By analytically examining the impact of graph structure on parameter-based gradient descent during training, and recasting the evolution of GCNs--shaped by parameter updates--through functional gradient descent in nonparametric teaching, we show for the first time that teaching graph property learners (i.e., GCNs) is consistent with teaching structure-aware nonparametric learners. These new findings readily commit GraNT to enhancing learning efficiency of the graph property learner, showing significant reductions in training time for graph-level regression (-36.62%), graph-level classification (-38.19%), node-level regression (-30.97%) and node-level classification (-47.30%), all while maintaining its generalization performance.

A Survey of Learning on Small Data

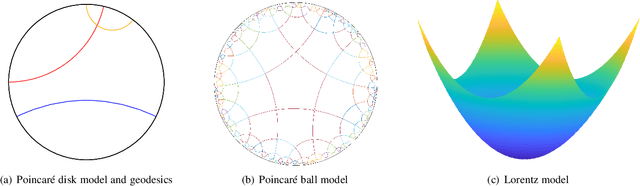
Learning on big data brings success for artificial intelligence (AI), but the annotation and training costs are expensive. In future, learning on small data is one of the ultimate purposes of AI, which requires machines to recognize objectives and scenarios relying on small data as humans. A series of machine learning models is going on this way such as active learning, few-shot learning, deep clustering. However, there are few theoretical guarantees for their generalization performance. Moreover, most of their settings are passive, that is, the label distribution is explicitly controlled by one specified sampling scenario. This survey follows the agnostic active sampling under a PAC (Probably Approximately Correct) framework to analyze the generalization error and label complexity of learning on small data using a supervised and unsupervised fashion. With these theoretical analyses, we categorize the small data learning models from two geometric perspectives: the Euclidean and non-Euclidean (hyperbolic) mean representation, where their optimization solutions are also presented and discussed. Later, some potential learning scenarios that may benefit from small data learning are then summarized, and their potential learning scenarios are also analyzed. Finally, some challenging applications such as computer vision, natural language processing that may benefit from learning on small data are also surveyed.