Geometric Learning Dynamics

We present a unified geometric framework for modeling learning dynamics in physical, biological, and machine learning systems. The theory reveals three fundamental regimes, each emerging from the power-law relationship $g \propto \kappa^a$ between the metric tensor $g$ in the space of trainable variables and the noise covariance matrix $\kappa$. The quantum regime corresponds to $a = 1$ and describes Schr\"odinger-like dynamics that emerges from a discrete shift symmetry. The efficient learning regime corresponds to $a = \tfrac{1}{2}$ and describes very fast machine learning algorithms. The equilibration regime corresponds to $a = 0$ and describes classical models of biological evolution. We argue that the emergence of the intermediate regime $a = \tfrac{1}{2}$ is a key mechanism underlying the emergence of biological complexity.

Molecular Learning Dynamics

We apply the physics-learning duality to molecular systems by complementing the physical description of interacting particles with a dual learning description, where each particle is modeled as an agent minimizing a loss function. In the traditional physics framework, the equations of motion are derived from the Lagrangian function, while in the learning framework, the same equations emerge from learning dynamics driven by the agent loss function. The loss function depends on scalar quantities that describe invariant properties of all other agents or particles. To demonstrate this approach, we first infer the loss functions of oxygen and hydrogen directly from a dataset generated by the CP2K physics-based simulation of water molecules. We then employ the loss functions to develop a learning-based simulation of water molecules, which achieves comparable accuracy while being significantly more computationally efficient than standard physics-based simulations.

Covariant Gradient Descent

We present a manifestly covariant formulation of the gradient descent method, ensuring consistency across arbitrary coordinate systems and general curved trainable spaces. The optimization dynamics is defined using a covariant force vector and a covariant metric tensor, both computed from the first and second statistical moments of the gradients. These moments are estimated through time-averaging with an exponential weight function, which preserves linear computational complexity. We show that commonly used optimization methods such as RMSProp, Adam and AdaBelief correspond to special limits of the covariant gradient descent (CGD) and demonstrate how these methods can be further generalized and improved.

Emergent field theories from neural networks

We establish a duality relation between Hamiltonian systems and neural network-based learning systems. We show that the Hamilton-Jacobi equations for position and momentum variables correspond to the equations governing the activation dynamics of non-trainable variables and the learning dynamics of trainable variables. The duality is then applied to model various field theories using the activation and learning dynamics of neural networks. For Klein-Gordon fields, the corresponding weight tensor is symmetric, while for Dirac fields, the weight tensor must contain an anti-symmetric tensor factor. The dynamical components of the weight and bias tensors correspond, respectively, to the temporal and spatial components of the gauge field.

Dataset-learning duality and emergent criticality

In artificial neural networks, the activation dynamics of non-trainable variables is strongly coupled to the learning dynamics of trainable variables. During the activation pass, the boundary neurons (e.g., input neurons) are mapped to the bulk neurons (e.g., hidden neurons), and during the learning pass, both bulk and boundary neurons are mapped to changes in trainable variables (e.g., weights and biases). For example, in feed-forward neural networks, forward propagation is the activation pass and backward propagation is the learning pass. We show that a composition of the two maps establishes a duality map between a subspace of non-trainable boundary variables (e.g., dataset) and a tangent subspace of trainable variables (i.e., learning). In general, the dataset-learning duality is a complex non-linear map between high-dimensional spaces, but in a learning equilibrium, the problem can be linearized and reduced to many weakly coupled one-dimensional problems. We use the duality to study the emergence of criticality, or the power-law distributions of fluctuations of the trainable variables. In particular, we show that criticality can emerge in the learning system even from the dataset in a non-critical state, and that the power-law distribution can be modified by changing either the activation function or the loss function.

Autonomous particles

Consider a reinforcement learning problem where an agent has access to a very large amount of information about the environment, but it can only take very few actions to accomplish its task and to maximize its reward. Evidently, the main problem for the agent is to learn a map from a very high-dimensional space (which represents its environment) to a very low-dimensional space (which represents its actions). The high-to-low dimensional map implies that most of the information about the environment is irrelevant for the actions to be taken, and only a small fraction of information is relevant. In this paper we argue that the relevant information need not be learned by brute force (which is the standard approach), but can be identified from the intrinsic symmetries of the system. We analyze in details a reinforcement learning problem of autonomous driving, where the corresponding symmetry is the Galilean symmetry, and argue that the learning task can be accomplished with very few relevant parameters, or, more precisely, invariants. For a numerical demonstration, we show that the autonomous vehicles (which we call autonomous particles since they describe very primitive vehicles) need only four relevant invariants to learn how to drive very well without colliding with other particles. The simple model can be easily generalized to include different types of particles (e.g. for cars, for pedestrians, for buildings, for road signs, etc.) with different types of relevant invariants describing interactions between them. We also argue that there must exist a field theory description of the learning system where autonomous particles would be described by fermionic degrees of freedom and interactions mediated by the relevant invariants would be described by bosonic degrees of freedom.

Bio-inspired Machine Learning: programmed death and replication

We analyze algorithmic and computational aspects of biological phenomena, such as replication and programmed death, in the context of machine learning. We use two different measures of neuron efficiency to develop machine learning algorithms for adding neurons to the system (i.e. replication algorithm) and removing neurons from the system (i.e. programmed death algorithm). We argue that the programmed death algorithm can be used for compression of neural networks and the replication algorithm can be used for improving performance of the already trained neural networks. We also show that a combined algorithm of programmed death and replication can improve the learning efficiency of arbitrary machine learning systems. The computational advantages of the bio-inspired algorithms are demonstrated by training feedforward neural networks on the MNIST dataset of handwritten images.

Towards a theory of quantum gravity from neural networks

Neural network is a dynamical system described by two different types of degrees of freedom: fast-changing non-trainable variables (e.g. state of neurons) and slow-changing trainable variables (e.g. weights and biases). We show that the non-equilibrium dynamics of trainable variables can be described by the Madelung equations, if the number of neurons is fixed, and by the Schrodinger equation, if the learning system is capable of adjusting its own parameters such as the number of neurons, step size and mini-batch size. We argue that the Lorentz symmetries and curved space-time can emerge from the interplay between stochastic entropy production and entropy destruction due to learning. We show that the non-equilibrium dynamics of non-trainable variables can be described by the geodesic equation (in the emergent space-time) for localized states of neurons, and by the Einstein equations (with cosmological constant) for the entire network. We conclude that the quantum description of trainable variables and the gravitational description of non-trainable variables are dual in the sense that they provide alternative macroscopic descriptions of the same learning system, defined microscopically as a neural network.

Thermodynamics of Evolution and the Origin of Life

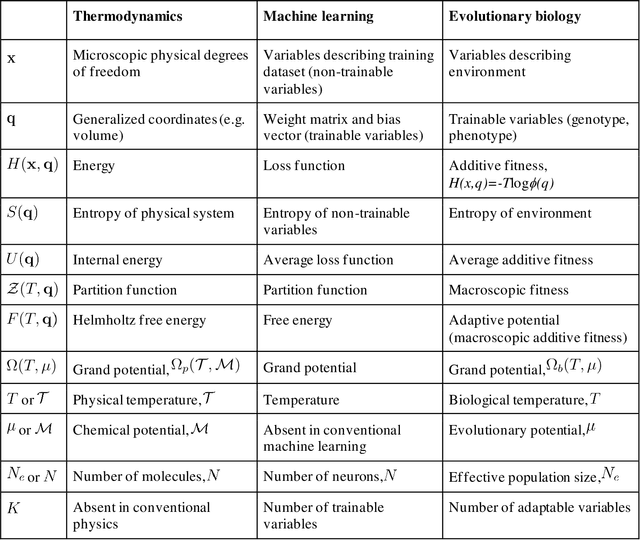
We outline a phenomenological theory of evolution and origin of life by combining the formalism of classical thermodynamics with a statistical description of learning. The maximum entropy principle constrained by the requirement for minimization of the loss function is employed to derive a canonical ensemble of organisms (population), the corresponding partition function (macroscopic counterpart of fitness) and free energy (macroscopic counterpart of additive fitness). We further define the biological counterparts of temperature (biological temperature) as the measure of stochasticity of the evolutionary process and of chemical potential (evolutionary potential) as the amount of evolutionary work required to add a new trainable variable (such as an additional gene) to the evolving system. We then develop a phenomenological approach to the description of evolution, which involves modeling the grand potential as a function of the biological temperature and evolutionary potential. We demonstrate how this phenomenological approach can be used to study the "ideal mutation" model of evolution and its generalizations. Finally, we show that, within this thermodynamics framework, major transitions in evolution, such as the transition from an ensemble of molecules to an ensemble of organisms, that is, the origin of life, can be modeled as a special case of bona fide physical phase transitions that are associated with the emergence of a new type of grand canonical ensemble and the corresponding new level of description

Towards a Theory of Evolution as Multilevel Learning

We apply the theory of learning to physically renormalizable systems in an attempt to develop a theory of biological evolution, including the origin of life, as multilevel learning. We formulate seven fundamental principles of evolution that appear to be necessary and sufficient to render a universe observable and show that they entail the major features of biological evolution, including replication and natural selection. These principles also follow naturally from the theory of learning. We formulate the theory of evolution using the mathematical framework of neural networks, which provides for detailed analysis of evolutionary phenomena. To demonstrate the potential of the proposed theoretical framework, we derive a generalized version of the Central Dogma of molecular biology by analyzing the flow of information during learning (back-propagation) and predicting (forward-propagation) the environment by evolving organisms. The more complex evolutionary phenomena, such as major transitions in evolution, in particular, the origin of life, have to be analyzed in the thermodynamic limit, which is described in detail in the accompanying paper.