Multi-scale structural complexity as a quantitative measure of visual complexity

While intuitive for humans, the concept of visual complexity is hard to define and quantify formally. We suggest adopting the multi-scale structural complexity (MSSC) measure, an approach that defines structural complexity of an object as the amount of dissimilarities between distinct scales in its hierarchical organization. In this work, we apply MSSC to the case of visual stimuli, using an open dataset of images with subjective complexity scores obtained from human participants (SAVOIAS). We demonstrate that MSSC correlates with subjective complexity on par with other computational complexity measures, while being more intuitive by definition, consistent across categories of images, and easier to compute. We discuss objective and subjective elements inherently present in human perception of complexity and the domains where the two are more likely to diverge. We show how the multi-scale nature of MSSC allows further investigation of complexity as it is perceived by humans.

Thermodynamics of Evolution and the Origin of Life

We outline a phenomenological theory of evolution and origin of life by combining the formalism of classical thermodynamics with a statistical description of learning. The maximum entropy principle constrained by the requirement for minimization of the loss function is employed to derive a canonical ensemble of organisms (population), the corresponding partition function (macroscopic counterpart of fitness) and free energy (macroscopic counterpart of additive fitness). We further define the biological counterparts of temperature (biological temperature) as the measure of stochasticity of the evolutionary process and of chemical potential (evolutionary potential) as the amount of evolutionary work required to add a new trainable variable (such as an additional gene) to the evolving system. We then develop a phenomenological approach to the description of evolution, which involves modeling the grand potential as a function of the biological temperature and evolutionary potential. We demonstrate how this phenomenological approach can be used to study the "ideal mutation" model of evolution and its generalizations. Finally, we show that, within this thermodynamics framework, major transitions in evolution, such as the transition from an ensemble of molecules to an ensemble of organisms, that is, the origin of life, can be modeled as a special case of bona fide physical phase transitions that are associated with the emergence of a new type of grand canonical ensemble and the corresponding new level of description

Towards a Theory of Evolution as Multilevel Learning

We apply the theory of learning to physically renormalizable systems in an attempt to develop a theory of biological evolution, including the origin of life, as multilevel learning. We formulate seven fundamental principles of evolution that appear to be necessary and sufficient to render a universe observable and show that they entail the major features of biological evolution, including replication and natural selection. These principles also follow naturally from the theory of learning. We formulate the theory of evolution using the mathematical framework of neural networks, which provides for detailed analysis of evolutionary phenomena. To demonstrate the potential of the proposed theoretical framework, we derive a generalized version of the Central Dogma of molecular biology by analyzing the flow of information during learning (back-propagation) and predicting (forward-propagation) the environment by evolving organisms. The more complex evolutionary phenomena, such as major transitions in evolution, in particular, the origin of life, have to be analyzed in the thermodynamic limit, which is described in detail in the accompanying paper.

Self-organized criticality in neural networks

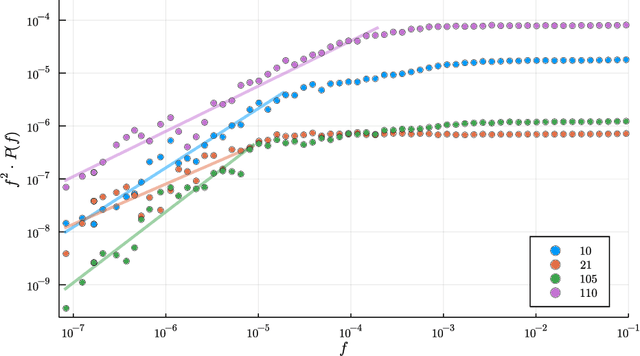
We demonstrate, both analytically and numerically, that learning dynamics of neural networks is generically attracted towards a self-organized critical state. The effect can be modeled with quartic interactions between non-trainable variables (e.g. states of neurons) and trainable variables (e.g. weight matrix). Non-trainable variables are rapidly driven towards stochastic equilibrium and trainable variables are slowly driven towards learning equilibrium described by a scale-invariant distribution on a wide range of scales. Our results suggest that the scale invariance observed in many physical and biological systems might be due to some kind of learning dynamics and support the claim that the universe might be a neural network.

Emergent Quantumness in Neural Networks

It was recently shown that the Madelung equations, that is, a hydrodynamic form of the Schr\"odinger equation, can be derived from a canonical ensemble of neural networks where the quantum phase was identified with the free energy of hidden variables. We consider instead a grand canonical ensemble of neural networks, by allowing an exchange of neurons with an auxiliary subsystem, to show that the free energy must also be multivalued. By imposing the multivaluedness condition on the free energy we derive the Schr\"odinger equation with "Planck's constant" determined by the chemical potential of hidden variables. This shows that quantum mechanics provides a correct statistical description of the dynamics of the grand canonical ensemble of neural networks at the learning equilibrium. We also discuss implications of the results for machine learning, fundamental physics and, in a more speculative way, evolutionary biology.