Thermodynamics of Evolution and the Origin of Life

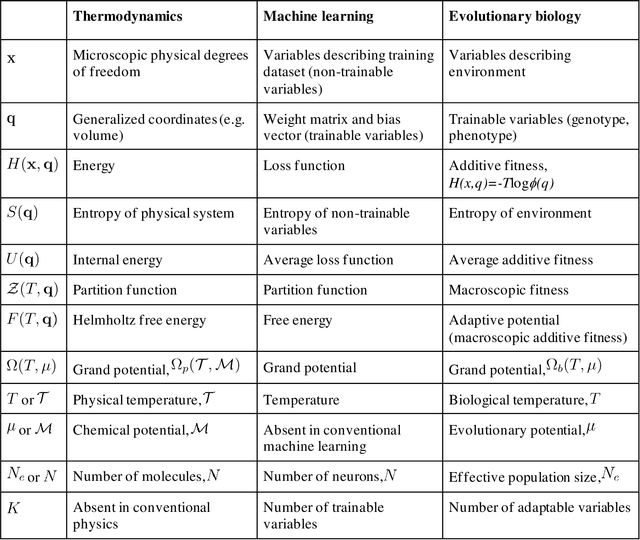
We outline a phenomenological theory of evolution and origin of life by combining the formalism of classical thermodynamics with a statistical description of learning. The maximum entropy principle constrained by the requirement for minimization of the loss function is employed to derive a canonical ensemble of organisms (population), the corresponding partition function (macroscopic counterpart of fitness) and free energy (macroscopic counterpart of additive fitness). We further define the biological counterparts of temperature (biological temperature) as the measure of stochasticity of the evolutionary process and of chemical potential (evolutionary potential) as the amount of evolutionary work required to add a new trainable variable (such as an additional gene) to the evolving system. We then develop a phenomenological approach to the description of evolution, which involves modeling the grand potential as a function of the biological temperature and evolutionary potential. We demonstrate how this phenomenological approach can be used to study the "ideal mutation" model of evolution and its generalizations. Finally, we show that, within this thermodynamics framework, major transitions in evolution, such as the transition from an ensemble of molecules to an ensemble of organisms, that is, the origin of life, can be modeled as a special case of bona fide physical phase transitions that are associated with the emergence of a new type of grand canonical ensemble and the corresponding new level of description

Towards a Theory of Evolution as Multilevel Learning

We apply the theory of learning to physically renormalizable systems in an attempt to develop a theory of biological evolution, including the origin of life, as multilevel learning. We formulate seven fundamental principles of evolution that appear to be necessary and sufficient to render a universe observable and show that they entail the major features of biological evolution, including replication and natural selection. These principles also follow naturally from the theory of learning. We formulate the theory of evolution using the mathematical framework of neural networks, which provides for detailed analysis of evolutionary phenomena. To demonstrate the potential of the proposed theoretical framework, we derive a generalized version of the Central Dogma of molecular biology by analyzing the flow of information during learning (back-propagation) and predicting (forward-propagation) the environment by evolving organisms. The more complex evolutionary phenomena, such as major transitions in evolution, in particular, the origin of life, have to be analyzed in the thermodynamic limit, which is described in detail in the accompanying paper.