Towards Quantum Advantage on Noisy Quantum Computers

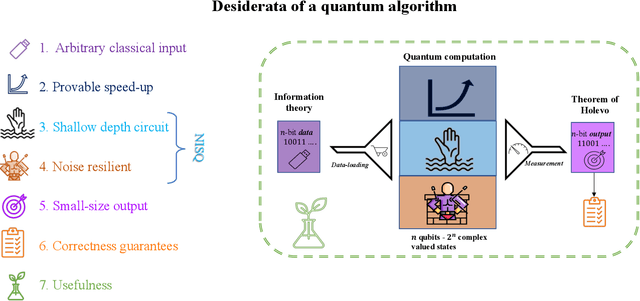
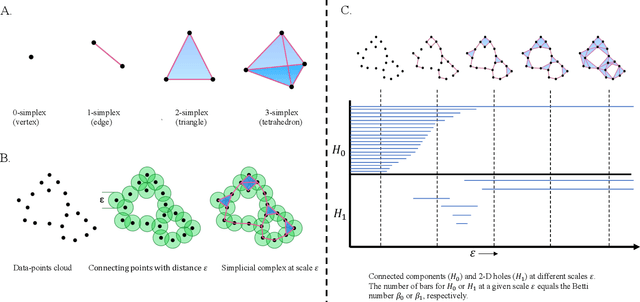
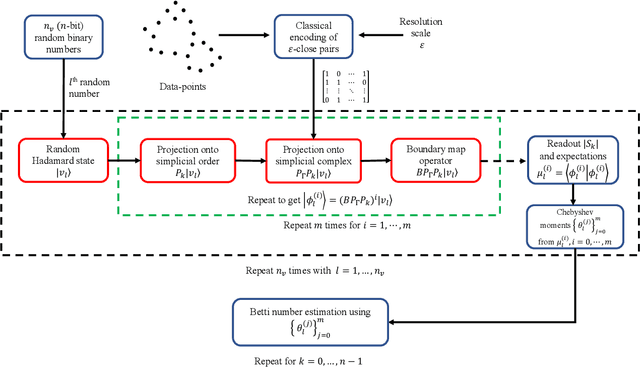
Topological data analysis (TDA) is a powerful technique for extracting complex and valuable shape-related summaries of high-dimensional data. However, the computational demands of classical TDA algorithms are exorbitant, and quickly become impractical for high-order characteristics. Quantum computing promises exponential speedup for certain problems. Yet, many existing quantum algorithms with notable asymptotic speedups require a degree of fault tolerance that is currently unavailable. In this paper, we present NISQ-TDA, the first fully implemented end-to-end quantum machine learning algorithm needing only a linear circuit-depth, that is applicable to non-handcrafted high-dimensional classical data, with potential speedup under stringent conditions. The algorithm neither suffers from the data-loading problem nor does it need to store the input data on the quantum computer explicitly. Our approach includes three key innovations: (a) an efficient realization of the full boundary operator as a sum of Pauli operators; (b) a quantum rejection sampling and projection approach to restrict a uniform superposition to the simplices of the desired order in the complex; and (c) a stochastic rank estimation method to estimate the topological features in the form of approximate Betti numbers. We present theoretical results that establish additive error guarantees for NISQ-TDA, and the circuit and computational time and depth complexities for exponentially scaled output estimates, up to the error tolerance. The algorithm was successfully executed on quantum computing devices, as well as on noisy quantum simulators, applied to small datasets. Preliminary empirical results suggest that the algorithm is robust to noise.

Quantum Topological Data Analysis with Linear Depth and Exponential Speedup

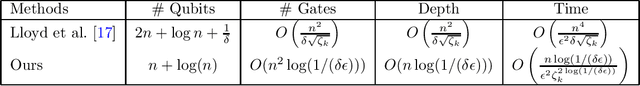
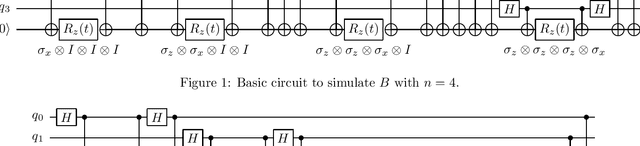
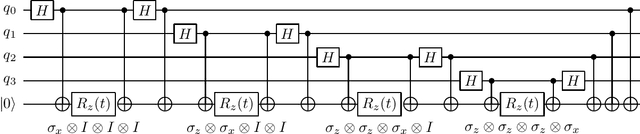
Quantum computing offers the potential of exponential speedups for certain classical computations. Over the last decade, many quantum machine learning (QML) algorithms have been proposed as candidates for such exponential improvements. However, two issues unravel the hope of exponential speedup for some of these QML algorithms: the data-loading problem and, more recently, the stunning dequantization results of Tang et al. A third issue, namely the fault-tolerance requirements of most QML algorithms, has further hindered their practical realization. The quantum topological data analysis (QTDA) algorithm of Lloyd, Garnerone and Zanardi was one of the first QML algorithms that convincingly offered an expected exponential speedup. From the outset, it did not suffer from the data-loading problem. A recent result has also shown that the generalized problem solved by this algorithm is likely classically intractable, and would therefore be immune to any dequantization efforts. However, the QTDA algorithm of Lloyd et~al. has a time complexity of $O(n^4/(\epsilon^2 \delta))$ (where $n$ is the number of data points, $\epsilon$ is the error tolerance, and $\delta$ is the smallest nonzero eigenvalue of the restricted Laplacian) and requires fault-tolerant quantum computing, which has not yet been achieved. In this paper, we completely overhaul the QTDA algorithm to achieve an improved exponential speedup and depth complexity of $O(n\log(1/(\delta\epsilon)))$. Our approach includes three key innovations: (a) an efficient realization of the combinatorial Laplacian as a sum of Pauli operators; (b) a quantum rejection sampling approach to restrict the superposition to the simplices in the complex; and (c) a stochastic rank estimation method to estimate the Betti numbers. We present a theoretical error analysis, and the circuit and computational time and depth complexities for Betti number estimation.

Logical Neural Networks

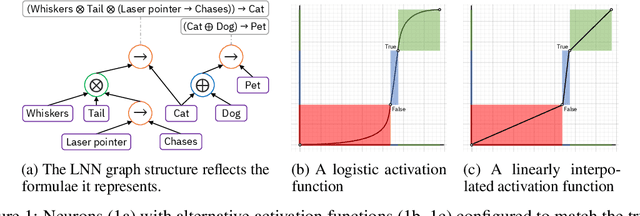
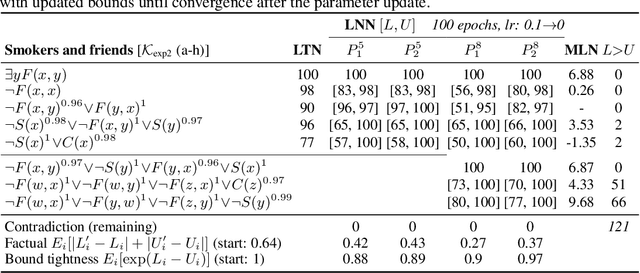
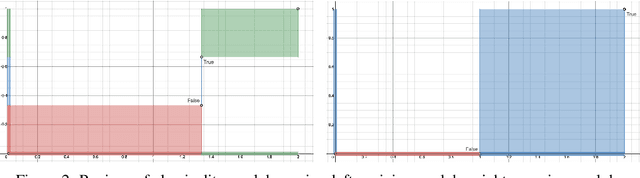
We propose a novel framework seamlessly providing key properties of both neural nets (learning) and symbolic logic (knowledge and reasoning). Every neuron has a meaning as a component of a formula in a weighted real-valued logic, yielding a highly intepretable disentangled representation. Inference is omnidirectional rather than focused on predefined target variables, and corresponds to logical reasoning, including classical first-order logic theorem proving as a special case. The model is end-to-end differentiable, and learning minimizes a novel loss function capturing logical contradiction, yielding resilience to inconsistent knowledge. It also enables the open-world assumption by maintaining bounds on truth values which can have probabilistic semantics, yielding resilience to incomplete knowledge.