Breaking the waves: asymmetric random periodic features for low-bitrate kernel machines

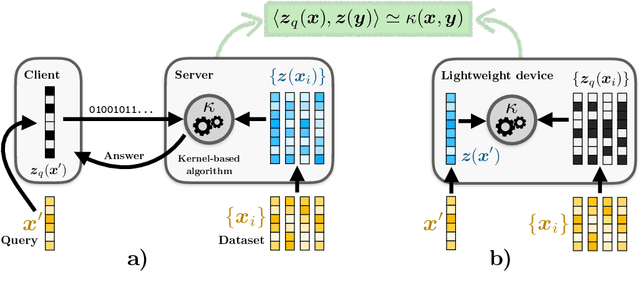
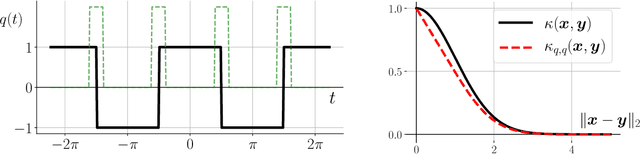
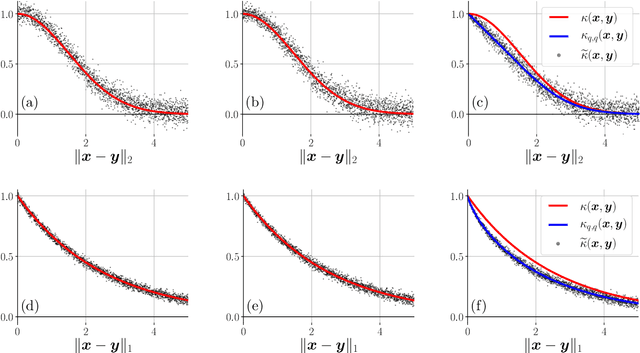
Many signal processing and machine learning applications are built from evaluating a kernel on pairs of signals, e.g. to assess the similarity of an incoming query to a database of known signals. This nonlinear evaluation can be simplified to a linear inner product of the random Fourier features of those signals: random projections followed by a periodic map, the complex exponential. It is known that a simple quantization of those features (corresponding to replacing the complex exponential by a different periodic map that takes binary values, which is appealing for their transmission and storage), distorts the approximated kernel, which may be undesirable in practice. Our take-home message is that when the features of only one of the two signals are quantized, the original kernel is recovered without distortion; its practical interest appears in several cases where the kernel evaluations are asymmetric by nature, such as a client-server scheme. Concretely, we introduce the general framework of asymmetric random periodic features, where the two signals of interest are observed through random periodic features: random projections followed by a general periodic map, which is allowed to be different for both signals. We derive the influence of those periodic maps on the approximated kernel, and prove uniform probabilistic error bounds holding for all signal pairs from an infinite low-complexity set. Interestingly, our results allow the periodic maps to be discontinuous, thanks to a new mathematical tool, i.e. the mean Lipschitz continuity. We then apply this generic framework to semi-quantized kernel machines (where only one signal has quantized features and the other has classical random Fourier features), for which we show theoretically that the approximated kernel remains unchanged (with the associated error bound), and confirm the power of the approach with numerical simulations.