Random features for Grassmannian kernel approximation with bounded rank-one projections

We propose a family of random feature maps for scalable kernel machines on low-dimensional subspaces, ie on the Grassmannian manifold. Such representations are useful when data classes or clusters are well described by the span of a few samples. Classical Grassmannian kernels, including the projection and Binet-Cauchy kernels, require full Gram matrices, which leads to prohibitive computational and memory costs for large high-dimensional subspace datasets. We address this limitation using random features based on rank-one projections of subspace projection matrices followed by bounded non-linear transforms, either periodic or binary, to control the resulting distributions. We show that inner products in the random feature space approximate well-defined rotation-invariant Grassmannian kernels that depend only on the principal angles between subspaces. When the number of features is sufficiently large relative to the intrinsic subspace dimension, the approximation holds uniformly over all fixed-dimensional subspaces with high probability. For periodic transforms, the approximated kernel has a closed-form expression with tunable behaviour between inverse Binet-Cauchy and Gaussian-type regimes. Binary transforms yield compact one-bit subspace features, although no closed-form kernel is known. Structured rank-one projections based on randomised fast Fourier transforms further reduce computation without sacrificing practical accuracy. Experiments on synthetic data and ETH-80 classification tasks show that these features accurately preserve Grassmannian geometry while reducing computation, memory, and storage. Rank-one embeddings therefore provide a practical and scalable alternative to classical Grassmannian kernels.

Random Features for Grassmannian Kernels

The Grassmannian manifold G(k, n) serves as a fundamental tool in signal processing, computer vision, and machine learning, where problems often involve classifying, clustering, or comparing subspaces. In this work, we propose a sketching-based approach to approximate Grassmannian kernels using random projections. We introduce three variations of kernel approximation, including two that rely on binarised sketches, offering substantial memory gains. We establish theoretical properties of our method in the special case of G(1, n) and extend it to general G(k, n). Experimental validation demonstrates that our sketched kernels closely match the performance of standard Grassmannian kernels while avoiding the need to compute or store the full kernel matrix. Our approach enables scalable Grassmannian-based methods for large-scale applications in machine learning and pattern recognition.

Signal processing after quadratic random sketching with optical units

Random data sketching (or projection) is now a classical technique enabling, for instance, approximate numerical linear algebra and machine learning algorithms with reduced computational complexity and memory. In this context, the possibility of performing data processing (such as pattern detection or classification) directly in the sketched domain without accessing the original data was previously achieved for linear random sketching methods and compressive sensing. In this work, we show how to estimate simple signal processing tasks (such as deducing local variations in a image) directly using random quadratic projections achieved by an optical processing unit. The same approach allows for naive data classification methods directly operated in the sketched domain. We report several experiments confirming the power of our approach.

Signal processing with optical quadratic random sketches

Random data sketching (or projection) is now a classical technique enabling, for instance, approximate numerical linear algebra and machine learning algorithms with reduced computational complexity and memory. In this context, the possibility of performing data processing (such as pattern detection or classification) directly in the sketched domain without accessing the original data was previously achieved for linear random sketching methods and compressive sensing. In this work, we show how to estimate simple signal processing tasks (such as deducing local variations in a image) directly using random quadratic projections achieved by an optical processing unit. The same approach allows for naive data classification methods directly operated in the sketched domain. We report several experiments confirming the power of our approach.

ROP inception: signal estimation with quadratic random sketching

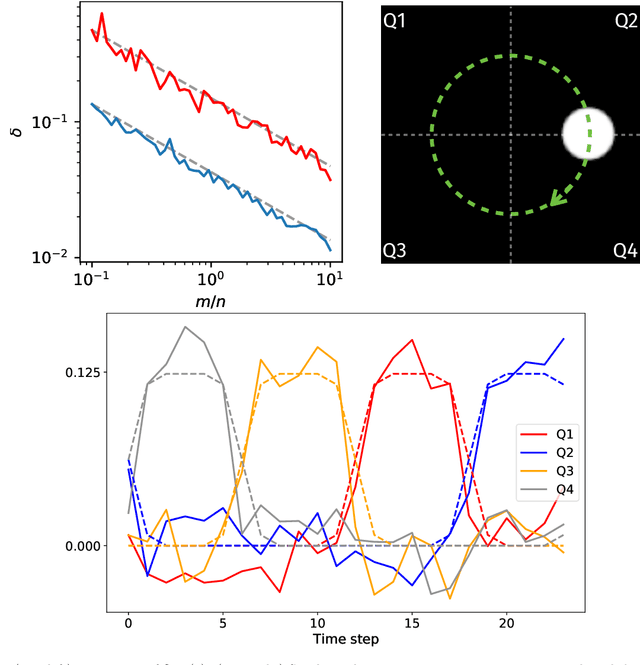
Rank-one projections (ROP) of matrices and quadratic random sketching of signals support several data processing and machine learning methods, as well as recent imaging applications, such as phase retrieval or optical processing units. In this paper, we demonstrate how signal estimation can be operated directly through such quadratic sketches--equivalent to the ROPs of the "lifted signal" obtained as its outer product with itself--without explicitly reconstructing that signal. Our analysis relies on showing that, up to a minor debiasing trick, the ROP measurement operator satisfies a generalised sign product embedding (SPE) property. In a nutshell, the SPE shows that the scalar product of a signal sketch with the "sign" of the sketch of a given pattern approximates the square of the projection of that signal on this pattern. This thus amounts to an insertion (an "inception") of a ROP model inside a ROP sketch. The effectiveness of our approach is evaluated in several synthetic experiments.