The potential role of AI agents in transforming nuclear medicine research and cancer management in India

India faces a significant cancer burden, with an incidence-to-mortality ratio indicating that nearly three out of five individuals diagnosed with cancer succumb to the disease. While the limitations of physical healthcare infrastructure are widely acknowledged as a primary challenge, concerted efforts by government and healthcare agencies are underway to mitigate these constraints. However, given the country's vast geography and high population density, it is imperative to explore alternative soft infrastructure solutions to complement existing frameworks. Artificial Intelligence agents are increasingly transforming problem-solving approaches across various domains, with their application in medicine proving particularly transformative. In this perspective, we examine the potential role of AI agents in advancing nuclear medicine for cancer research, diagnosis, and management in India. We begin with a brief overview of AI agents and their capabilities, followed by a proposed agent-based ecosystem that can address prevailing sustainability challenges in India nuclear medicine.

NeuroMorphix: A Novel Brain MRI Asymmetry-specific Feature Construction Approach For Seizure Recurrence Prediction

Seizure recurrence is an important concern after an initial unprovoked seizure; without drug treatment, it occurs within 2 years in 40-50% of cases. The decision to treat currently relies on predictors of seizure recurrence risk that are inaccurate, resulting in unnecessary, possibly harmful, treatment in some patients and potentially preventable seizures in others. Because of the link between brain lesions and seizure recurrence, we developed a recurrence prediction tool using machine learning and clinical 3T brain MRI. We developed NeuroMorphix, a feature construction approach based on MRI brain anatomy. Each of seven NeuroMorphix features measures the absolute or relative difference between corresponding regions in each cerebral hemisphere. FreeSurfer was used to segment brain regions and to generate values for morphometric parameters (8 for each cortical region and 5 for each subcortical region). The parameters were then mapped to whole brain NeuroMorphix features, yielding a total of 91 features per subject. Features were generated for a first seizure patient cohort (n = 169) categorised into seizure recurrence and non-recurrence subgroups. State-of-the-art classification algorithms were trained and tested using NeuroMorphix features to predict seizure recurrence. Classification models using the top 5 features, ranked by sequential forward selection, demonstrated excellent performance in predicting seizure recurrence, with area under the ROC curve of 88-93%, accuracy of 83-89%, and F1 score of 83-90%. Highly ranked features aligned with structural alterations known to be associated with epilepsy. This study highlights the potential for targeted, data-driven approaches to aid clinical decision-making in brain disorders.

Machine Learning Applications in Traumatic Brain Injury: A Spotlight on Mild TBI

Traumatic Brain Injury (TBI) poses a significant global public health challenge, contributing to high morbidity and mortality rates and placing a substantial economic burden on healthcare systems worldwide. The diagnosis of TBI relies on clinical information along with Computed Tomography (CT) scans. Addressing the multifaceted challenges posed by TBI has seen the development of innovative, data-driven approaches, for this complex condition. Particularly noteworthy is the prevalence of mild TBI (mTBI), which constitutes the majority of TBI cases where conventional methods often fall short. As such, we review the state-of-the-art Machine Learning (ML) techniques applied to clinical information and CT scans in TBI, with a particular focus on mTBI. We categorize ML applications based on their data sources, and there is a spectrum of ML techniques used to date. Most of these techniques have primarily focused on diagnosis, with relatively few attempts at predicting the prognosis. This review may serve as a source of inspiration for future research studies aimed at improving the diagnosis of TBI using data-driven approaches and standard diagnostic data.

Enhancing mTBI Diagnosis with Residual Triplet Convolutional Neural Network Using 3D CT

Mild Traumatic Brain Injury (mTBI) is a common and challenging condition to diagnose accurately. Timely and precise diagnosis is essential for effective treatment and improved patient outcomes. Traditional diagnostic methods for mTBI often have limitations in terms of accuracy and sensitivity. In this study, we introduce an innovative approach to enhance mTBI diagnosis using 3D Computed Tomography (CT) images and a metric learning technique trained with triplet loss. To address these challenges, we propose a Residual Triplet Convolutional Neural Network (RTCNN) model to distinguish between mTBI cases and healthy ones by embedding 3D CT scans into a feature space. The triplet loss function maximizes the margin between similar and dissimilar image pairs, optimizing feature representations. This facilitates better context placement of individual cases, aids informed decision-making, and has the potential to improve patient outcomes. Our RTCNN model shows promising performance in mTBI diagnosis, achieving an average accuracy of 94.3%, a sensitivity of 94.1%, and a specificity of 95.2%, as confirmed through a five-fold cross-validation. Importantly, when compared to the conventional Residual Convolutional Neural Network (RCNN) model, the RTCNN exhibits a significant improvement, showcasing a remarkable 22.5% increase in specificity, a notable 16.2% boost in accuracy, and an 11.3% enhancement in sensitivity. Moreover, RTCNN requires lower memory resources, making it not only highly effective but also resource-efficient in minimizing false positives while maximizing its diagnostic accuracy in distinguishing normal CT scans from mTBI cases. The quantitative performance metrics provided and utilization of occlusion sensitivity maps to visually explain the model's decision-making process further enhance the interpretability and transparency of our approach.

Interpretable 3D Multi-Modal Residual Convolutional Neural Network for Mild Traumatic Brain Injury Diagnosis

Mild Traumatic Brain Injury (mTBI) is a significant public health challenge due to its high prevalence and potential for long-term health effects. Despite Computed Tomography (CT) being the standard diagnostic tool for mTBI, it often yields normal results in mTBI patients despite symptomatic evidence. This fact underscores the complexity of accurate diagnosis. In this study, we introduce an interpretable 3D Multi-Modal Residual Convolutional Neural Network (MRCNN) for mTBI diagnostic model enhanced with Occlusion Sensitivity Maps (OSM). Our MRCNN model exhibits promising performance in mTBI diagnosis, demonstrating an average accuracy of 82.4%, sensitivity of 82.6%, and specificity of 81.6%, as validated by a five-fold cross-validation process. Notably, in comparison to the CT-based Residual Convolutional Neural Network (RCNN) model, the MRCNN shows an improvement of 4.4% in specificity and 9.0% in accuracy. We show that the OSM offers superior data-driven insights into CT images compared to the Grad-CAM approach. These results highlight the efficacy of the proposed multi-modal model in enhancing the diagnostic precision of mTBI.

Robust, fast and accurate mapping of diffusional mean kurtosis

Diffusion weighted magnetic resonance imaging produces data encoded with the random motion of water molecules in biological tissues. The collection and extraction of information from such data have become critical to modern imaging studies, and particularly those focusing on neuroimaging. A range of mathematical models are routinely applied to infer tissue microstructure properties. Diffusional kurtosis imaging entails a model for measuring the extent of non-Gaussian diffusion in biological tissues. The method has seen wide assimilation across a range of clinical applications, and promises to be an increasingly important tool for clinical diagnosis, treatment planning and monitoring. However, accurate and robust estimation of kurtosis from clinically feasible data acquisitions remains a challenge. We outline a fast and robust way of estimating mean kurtosis via the sub-diffusion mathematical framework. Our kurtosis mapping method is evaluated using simulations and the Connectome 1.0 human brain data. Results show that fitting the sub-diffusion model to multiple diffusion time data and then directly calculating the mean kurtosis greatly improves the quality of the estimation. Suggestions for diffusion encoding sampling, the number of diffusion times to be acquired and the separation between them are provided. Exquisite tissue contrast is achieved even when the diffusion encoded data is collected in only minutes. Our findings suggest robust estimation of mean kurtosis can be realised within a clinically feasible diffusion weighted magnetic resonance imaging data acquisition time.

Instant tissue field and magnetic susceptibility mapping from MR raw phase using Laplacian enabled deep neural networks

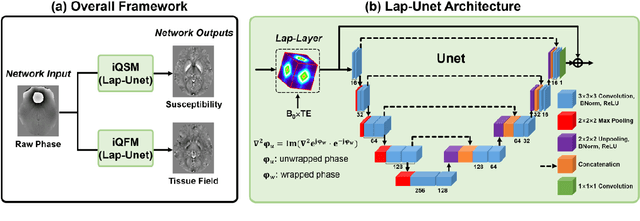
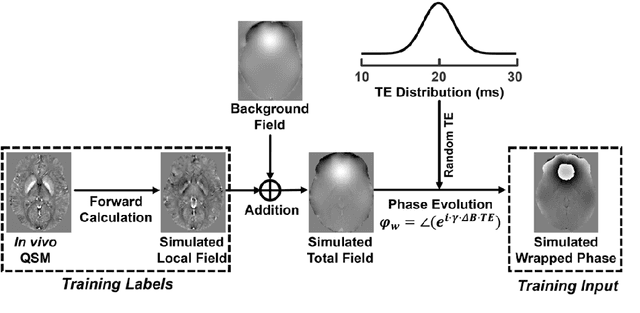
Quantitative susceptibility mapping (QSM) is a valuable MRI post-processing technique that quantifies the magnetic susceptibility of body tissue from phase data. However, the traditional QSM reconstruction pipeline involves multiple non-trivial steps, including phase unwrapping, background field removal, and dipole inversion. These intermediate steps not only increase the reconstruction time but amplify noise and errors. This study develops a large-stencil Laplacian preprocessed deep learning-based neural network for near instant quantitative field and susceptibility mapping (i.e., iQFM and iQSM) from raw MR phase data. The proposed iQFM and iQSM methods were compared with established reconstruction pipelines on simulated and in vivo datasets. In addition, experiments on patients with intracranial hemorrhage and multiple sclerosis were also performed to test the generalization of the novel neural networks. The proposed iQFM and iQSM methods yielded comparable results to multi-step methods in healthy subjects while dramatically improving reconstruction accuracies on intracranial hemorrhages with large susceptibilities. The reconstruction time was also substantially shortened from minutes using multi-step methods to only 30 milliseconds using the trained iQFM and iQSM neural networks.

Fractional order magnetic resonance fingerprinting in the human cerebral cortex

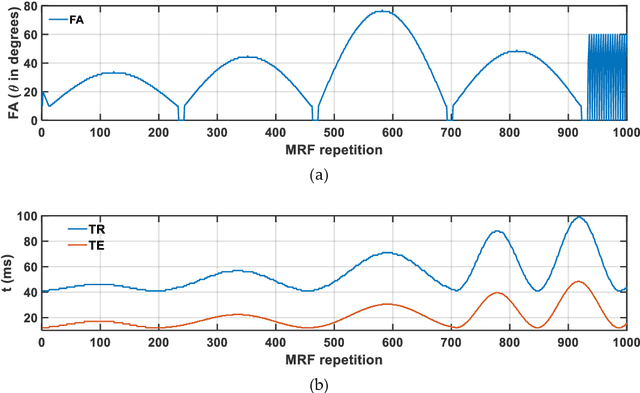
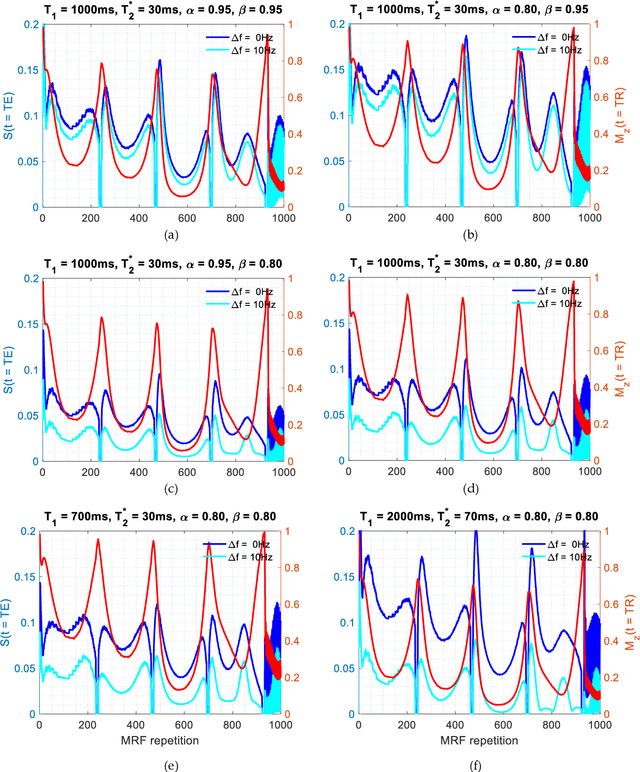
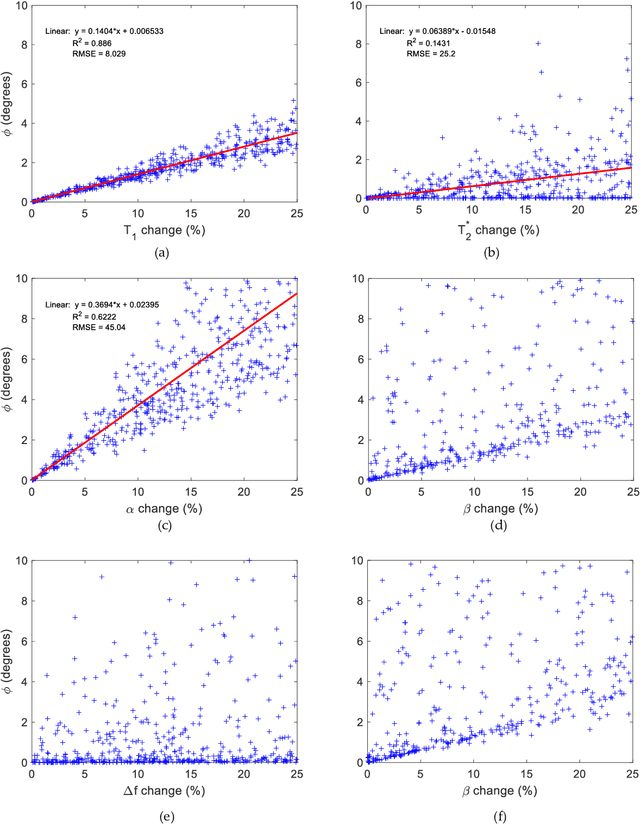
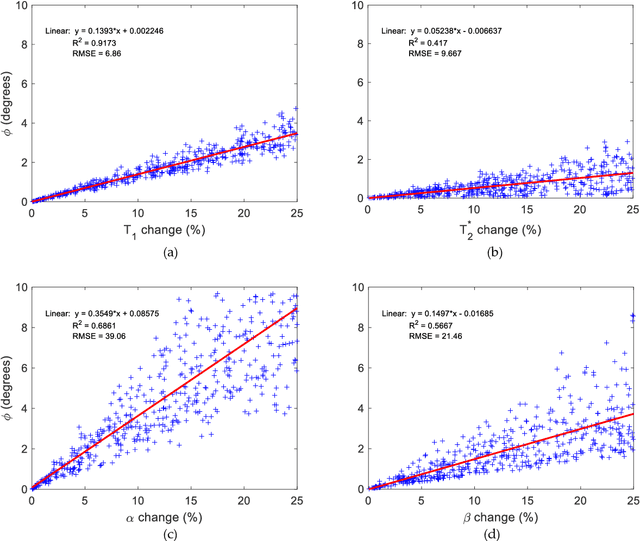
Mathematical models are becoming increasingly important in magnetic resonance imaging (MRI), as they provide a mechanistic approach for making a link between tissue microstructure and signals acquired using the medical imaging instrument. The Bloch equations, which describes spin and relaxation in a magnetic field, is a set of integer order differential equations with a solution exhibiting mono-exponential behaviour in time. Parameters of the model may be estimated using a non-linear solver, or by creating a dictionary of model parameters from which MRI signals are simulated and then matched with experiment. We have previously shown the potential efficacy of a magnetic resonance fingerprinting (MRF) approach, i.e. dictionary matching based on the classical Bloch equations, for parcellating the human cerebral cortex. However, this classical model is unable to describe in full the mm-scale MRI signal generated based on an heterogenous and complex tissue micro-environment. The time-fractional order Bloch equations has been shown to provide, as a function of time, a good fit of brain MRI signals. We replaced the integer order Bloch equations with the previously reported time-fractional counterpart within the MRF framework and performed experiments to parcellate human gray matter, which is cortical brain tissue with different cyto-architecture at different spatial locations. Our findings suggest that the time-fractional order parameters, {\alpha} and {\beta}, potentially associate with the effect of interareal architectonic variability, hypothetically leading to more accurate cortical parcellation.

CNNs and GANs in MRI-based cross-modality medical image estimation

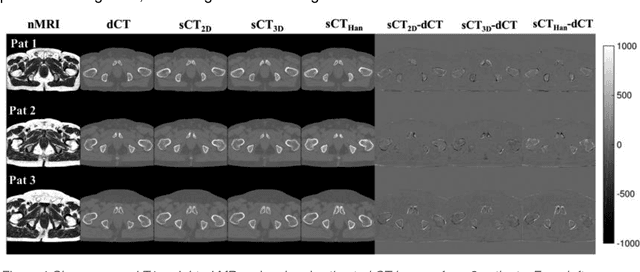
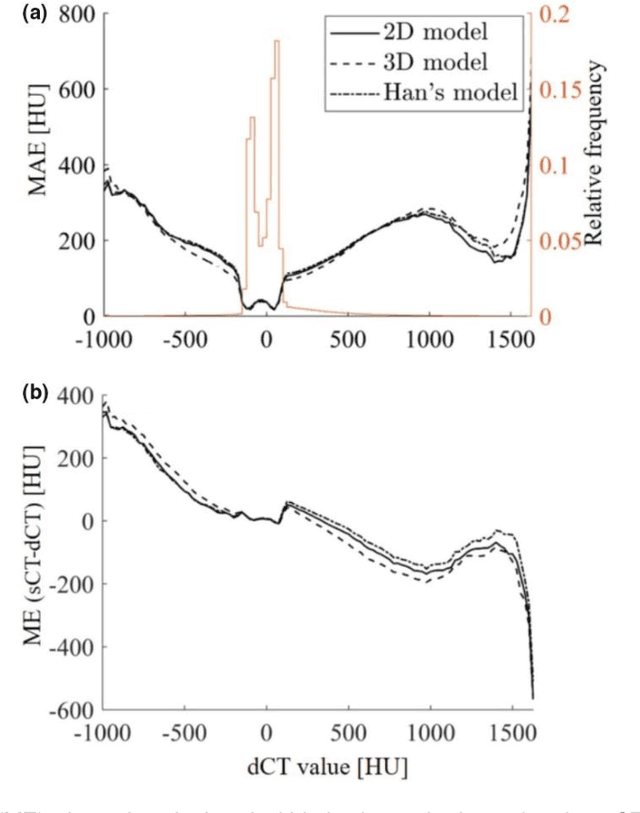
Cross-modality image estimation involves the generation of images of one medical imaging modality from that of another modality. Convolutional neural networks (CNNs) have been shown to be useful in identifying, characterising and extracting image patterns. Generative adversarial networks (GANs) use CNNs as generators and estimated images are discriminated as true or false based on an additional network. CNNs and GANs within the image estimation framework may be considered more generally as deep learning approaches, since imaging data tends to be large, leading to a larger number of network weights. Almost all research in the CNN/GAN image estimation literature has involved the use of MRI data with the other modality primarily being PET or CT. This review provides an overview of the use of CNNs and GANs for MRI-based cross-modality medical image estimation. We outline the neural networks implemented, and detail network constructs employed for CNN and GAN image-to-image estimators. Motivations behind cross-modality image estimation are provided as well. GANs appear to provide better utility in cross-modality image estimation in comparison with CNNs, a finding drawn based on our analysis involving metrics comparing estimated and actual images. Our final remarks highlight key challenges faced by the cross-modality medical image estimation field, and suggestions for future research are outlined.

Linear centralization classifier

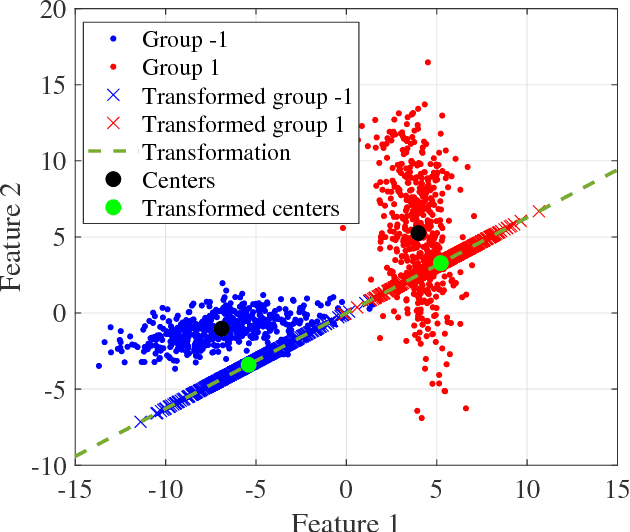
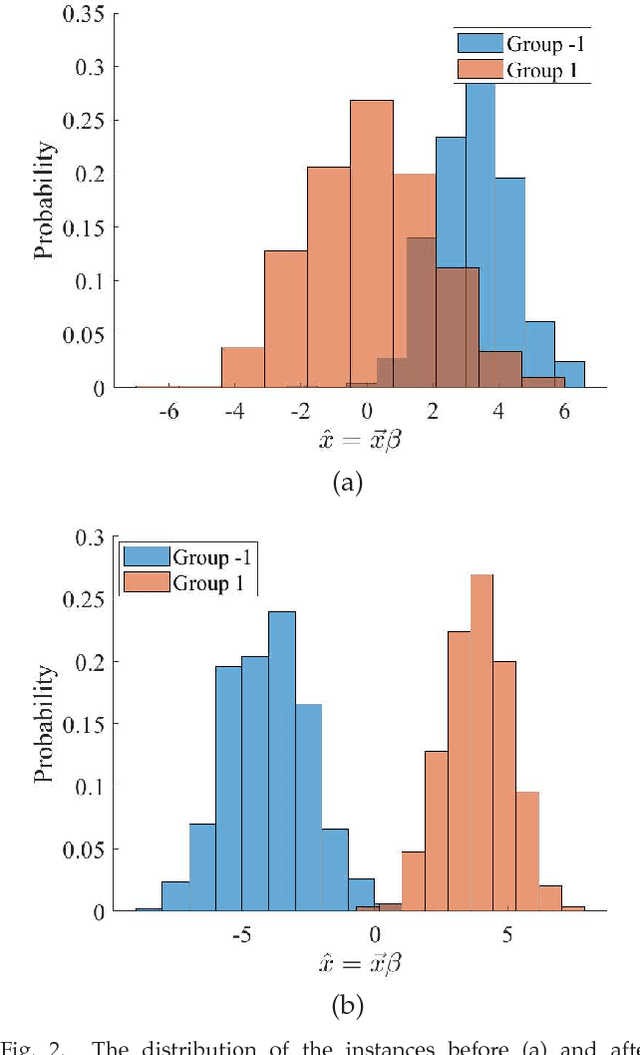
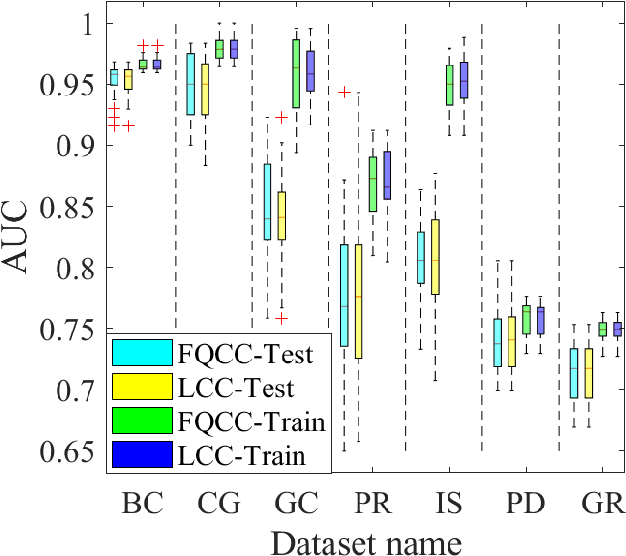
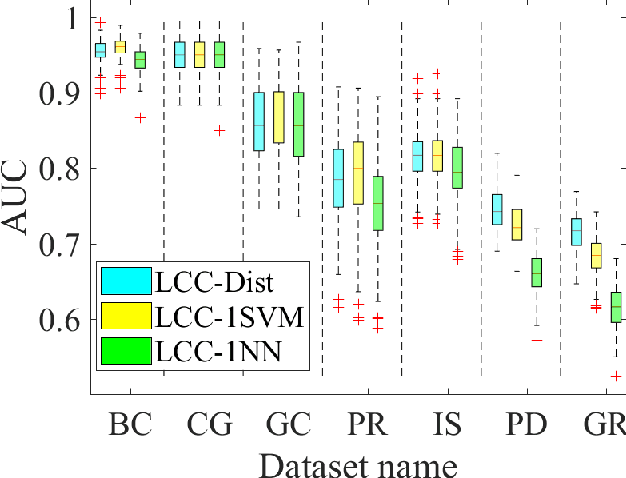
A classification algorithm, called the Linear Centralization Classifier (LCC), is introduced. The algorithm seeks to find a transformation that best maps instances from the feature space to a space where they concentrate towards the center of their own classes, while maximimizing the distance between class centers. We formulate the classifier as a quadratic program with quadratic constraints. We then simplify this formulation to a linear program that can be solved effectively using a linear programming solver (e.g., simplex-dual). We extend the formulation for LCC to enable the use of kernel functions for non-linear classification applications. We compare our method with two standard classification methods (support vector machine and linear discriminant analysis) and four state-of-the-art classification methods when they are applied to eight standard classification datasets. Our experimental results show that LCC is able to classify instances more accurately (based on the area under the receiver operating characteristic) in comparison to other tested methods on the chosen datasets. We also report the results for LCC with a particular kernel to solve for synthetic non-linear classification problems.