Quantum policy gradient algorithms

Understanding the power and limitations of quantum access to data in machine learning tasks is primordial to assess the potential of quantum computing in artificial intelligence. Previous works have already shown that speed-ups in learning are possible when given quantum access to reinforcement learning environments. Yet, the applicability of quantum algorithms in this setting remains very limited, notably in environments with large state and action spaces. In this work, we design quantum algorithms to train state-of-the-art reinforcement learning policies by exploiting quantum interactions with an environment. However, these algorithms only offer full quadratic speed-ups in sample complexity over their classical analogs when the trained policies satisfy some regularity conditions. Interestingly, we find that reinforcement learning policies derived from parametrized quantum circuits are well-behaved with respect to these conditions, which showcases the benefit of a fully-quantum reinforcement learning framework.

On establishing learning separations between classical and quantum machine learning with classical data

Despite years of effort, the quantum machine learning community has only been able to show quantum learning advantages for certain contrived cryptography-inspired datasets in the case of classical data. In this note, we discuss the challenges of finding learning problems that quantum learning algorithms can learn much faster than any classical learning algorithm, and we study how to identify such learning problems. Specifically, we reflect on the main concepts in computational learning theory pertaining to this question, and we discuss how subtle changes in definitions can mean conceptually significantly different tasks, which can either lead to a separation or no separation at all. Moreover, we study existing learning problems with a provable quantum speedup to distill sets of more general and sufficient conditions (i.e., ``checklists'') for a learning problem to exhibit a separation between classical and quantum learners. These checklists are intended to streamline one's approach to proving quantum speedups for learning problems, or to elucidate bottlenecks. Finally, to illustrate its application, we analyze examples of potential separations (i.e., when the learning problem is build from computational separations, or when the data comes from a quantum experiment) through the lens of our approach.

Reinforcement Learning Assisted Recursive QAOA

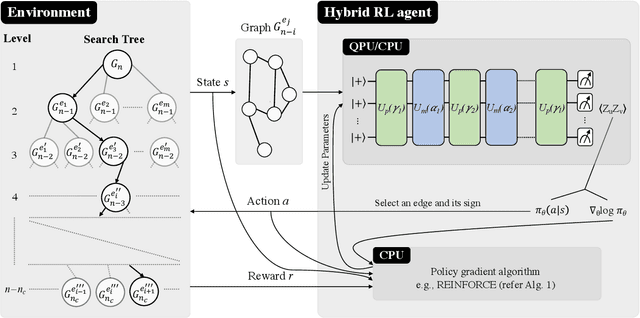
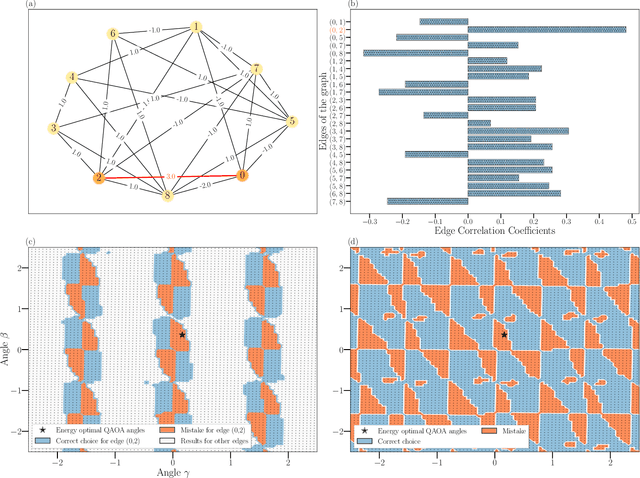
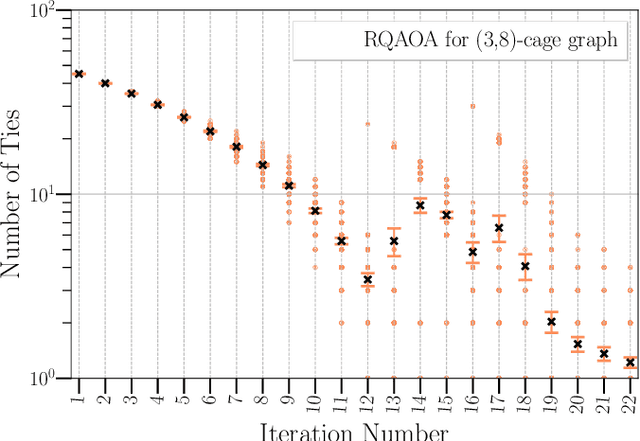
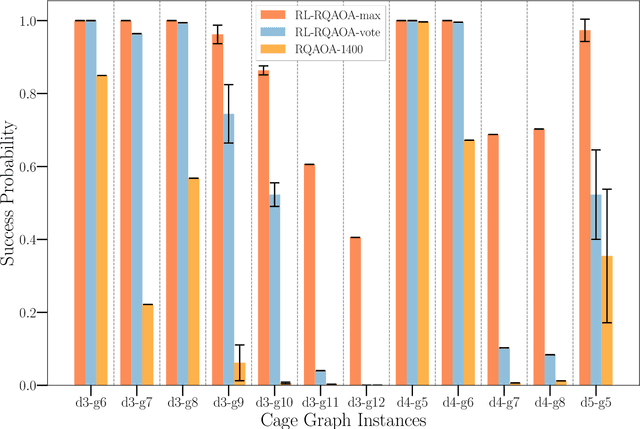
Variational quantum algorithms such as the Quantum Approximation Optimization Algorithm (QAOA) in recent years have gained popularity as they provide the hope of using NISQ devices to tackle hard combinatorial optimization problems. It is, however, known that at low depth, certain locality constraints of QAOA limit its performance. To go beyond these limitations, a non-local variant of QAOA, namely recursive QAOA (RQAOA), was proposed to improve the quality of approximate solutions. The RQAOA has been studied comparatively less than QAOA, and it is less understood, for instance, for what family of instances it may fail to provide high quality solutions. However, as we are tackling $\mathsf{NP}$-hard problems (specifically, the Ising spin model), it is expected that RQAOA does fail, raising the question of designing even better quantum algorithms for combinatorial optimization. In this spirit, we identify and analyze cases where RQAOA fails and, based on this, propose a reinforcement learning enhanced RQAOA variant (RL-RQAOA) that improves upon RQAOA. We show that the performance of RL-RQAOA improves over RQAOA: RL-RQAOA is strictly better on these identified instances where RQAOA underperforms, and is similarly performing on instances where RQAOA is near-optimal. Our work exemplifies the potentially beneficial synergy between reinforcement learning and quantum (inspired) optimization in the design of new, even better heuristics for hard problems.

Hyperparameter Importance of Quantum Neural Networks Across Small Datasets

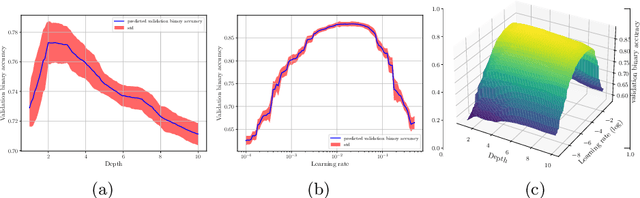
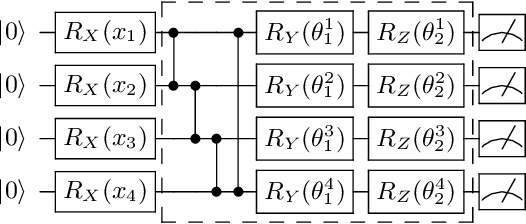
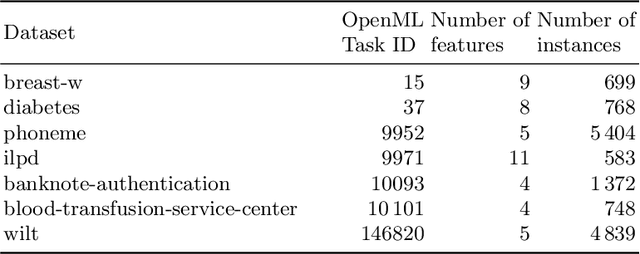
As restricted quantum computers are slowly becoming a reality, the search for meaningful first applications intensifies. In this domain, one of the more investigated approaches is the use of a special type of quantum circuit - a so-called quantum neural network -- to serve as a basis for a machine learning model. Roughly speaking, as the name suggests, a quantum neural network can play a similar role to a neural network. However, specifically for applications in machine learning contexts, very little is known about suitable circuit architectures, or model hyperparameters one should use to achieve good learning performance. In this work, we apply the functional ANOVA framework to quantum neural networks to analyze which of the hyperparameters were most influential for their predictive performance. We analyze one of the most typically used quantum neural network architectures. We then apply this to $7$ open-source datasets from the OpenML-CC18 classification benchmark whose number of features is small enough to fit on quantum hardware with less than $20$ qubits. Three main levels of importance were detected from the ranking of hyperparameters obtained with functional ANOVA. Our experiment both confirmed expected patterns and revealed new insights. For instance, setting well the learning rate is deemed the most critical hyperparameter in terms of marginal contribution on all datasets, whereas the particular choice of entangling gates used is considered the least important except on one dataset. This work introduces new methodologies to study quantum machine learning models and provides new insights toward quantum model selection.

Equivariant quantum circuits for learning on weighted graphs

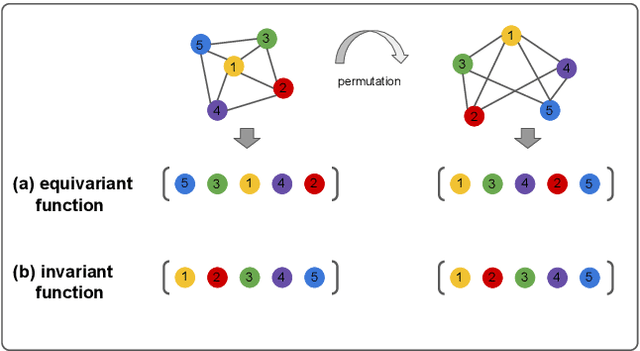
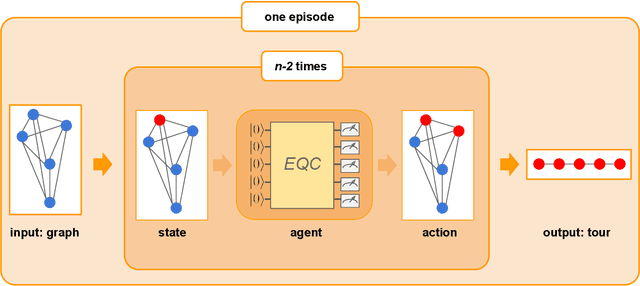
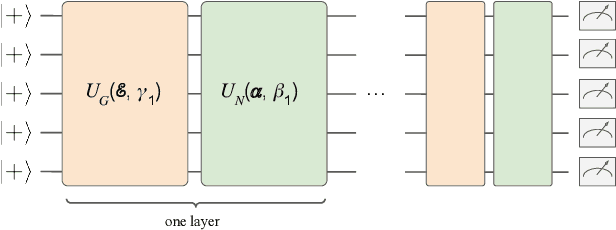
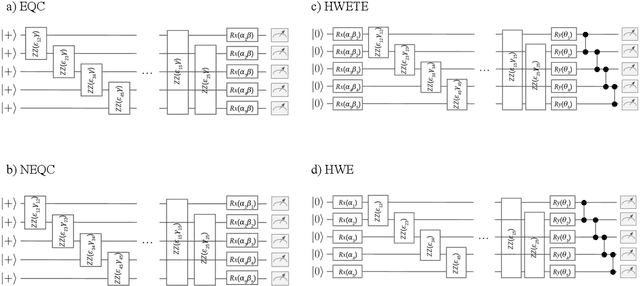
Variational quantum algorithms are the leading candidate for near-term advantage on noisy quantum hardware. When training a parametrized quantum circuit to solve a specific task, the choice of ansatz is one of the most important factors that determines the trainability and performance of the algorithm. Problem-tailored ansatzes have become the standard for tasks in optimization or quantum chemistry, and yield more efficient algorithms with better performance than unstructured approaches. In quantum machine learning (QML), however, the literature on ansatzes that are motivated by the training data structure is scarce. Considering that it is widely known that unstructured ansatzes can become untrainable with increasing system size and circuit depth, it is of key importance to also study problem-tailored circuit architectures in a QML context. In this work, we introduce an ansatz for learning tasks on weighted graphs that respects an important graph symmetry, namely equivariance under node permutations. We evaluate the performance of this ansatz on a complex learning task on weighted graphs, where a ML model is used to implement a heuristic for a combinatorial optimization problem. We analytically study the expressivity of our ansatz at depth one, and numerically compare the performance of our model on instances with up to 20 qubits to ansatzes where the equivariance property is gradually broken. We show that our ansatz outperforms all others even in the small-instance regime. Our results strengthen the notion that symmetry-preserving ansatzes are a key to success in QML and should be an active area of research in order to enable near-term advantages in this field.

High Dimensional Quantum Learning With Small Quantum Computers

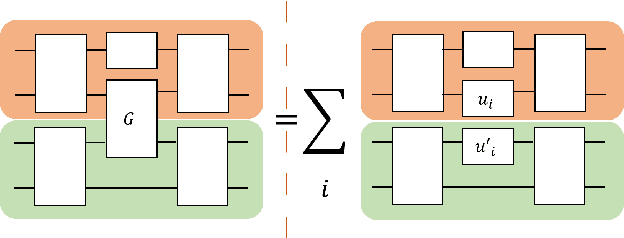
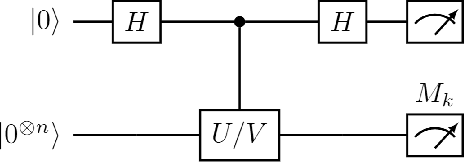
Quantum computers hold great promise to enhance machine learning, but their current qubit counts restrict the realisation of this promise. In an attempt to placate this limitation techniques can be applied for evaluating a quantum circuit using a machine with fewer qubits than the circuit naively requires. These techniques work by evaluating many smaller circuits on the smaller machine, that are then combined in a polynomial to replicate the output of the larger machine. This scheme requires more circuit evaluations than are practical for general circuits. However, we investigate the possibility that for certain applications many of these subcircuits are superfluous, and that a much smaller sum is sufficient to estimate the full circuit. We construct a machine learning model that may be capable of approximating the outputs of the larger circuit with much fewer circuit evaluations. We successfully apply our model to the task of digit recognition, using simulated quantum computers much smaller than the data dimension. The model is also applied to the task of approximating a random 10 qubit PQC with simulated access to a 5 qubit computer, even with only relatively modest number of circuits our model provides an accurate approximation of the 10 qubit PQCs output, superior to a neural network attempt. The developed method might be useful for implementing quantum models on larger data throughout the NISQ era.

Quantum machine learning beyond kernel methods

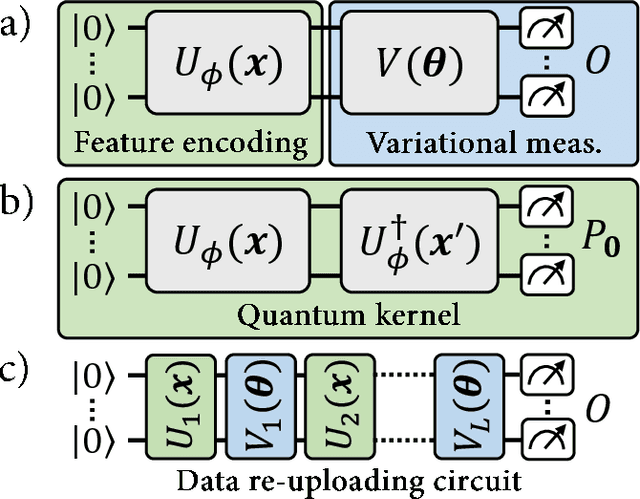
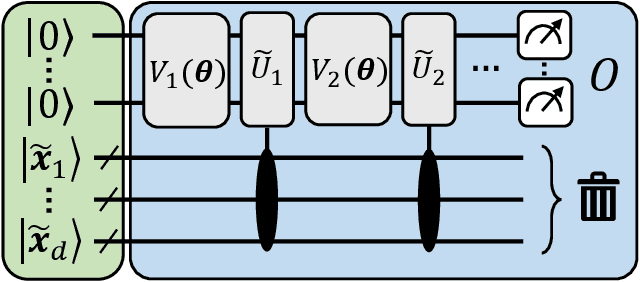
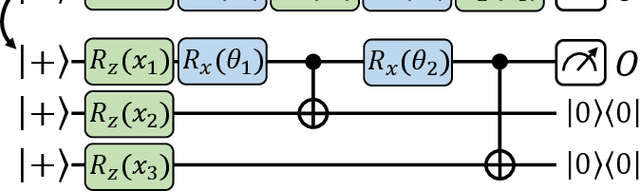
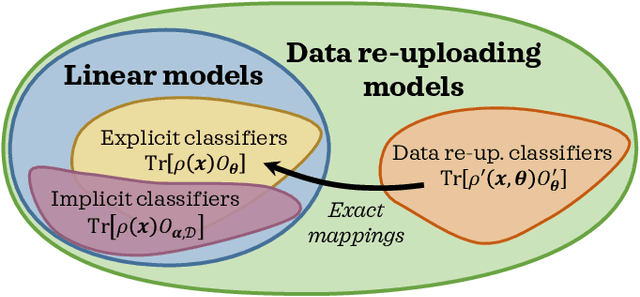
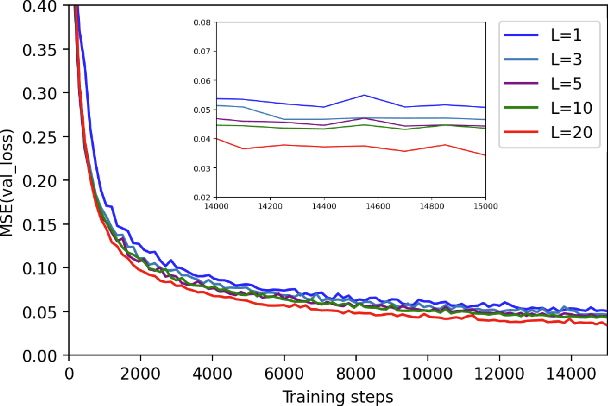
With noisy intermediate-scale quantum computers showing great promise for near-term applications, a number of machine learning algorithms based on parametrized quantum circuits have been suggested as possible means to achieve learning advantages. Yet, our understanding of how these quantum machine learning models compare, both to existing classical models and to each other, remains limited. A big step in this direction has been made by relating them to so-called kernel methods from classical machine learning. By building on this connection, previous works have shown that a systematic reformulation of many quantum machine learning models as kernel models was guaranteed to improve their training performance. In this work, we first extend the applicability of this result to a more general family of parametrized quantum circuit models called data re-uploading circuits. Secondly, we show, through simple constructions and numerical simulations, that models defined and trained variationally can exhibit a critically better generalization performance than their kernel formulations, which is the true figure of merit of machine learning tasks. Our results constitute another step towards a more comprehensive theory of quantum machine learning models next to kernel formulations.

Structural risk minimization for quantum linear classifiers

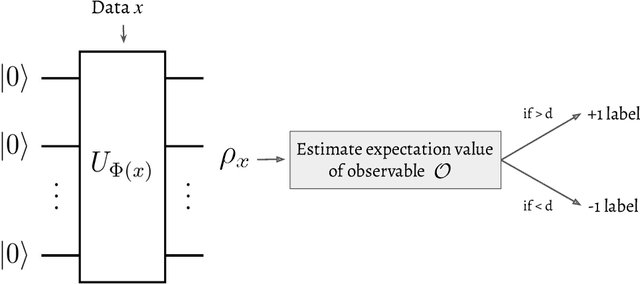
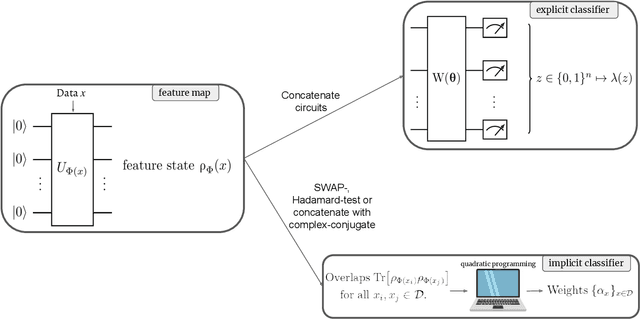
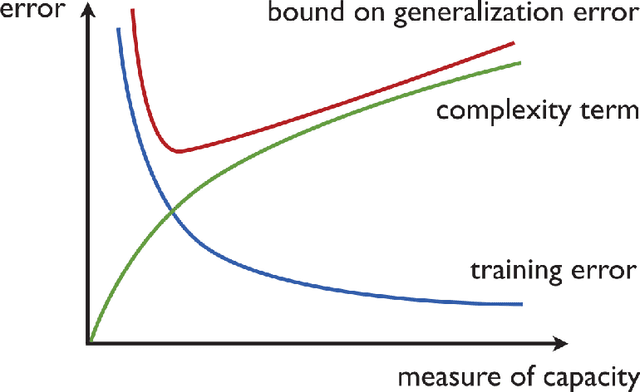
Quantum machine learning (QML) stands out as one of the typically highlighted candidates for quantum computing's near-term "killer application". In this context, QML models based on parameterized quantum circuits comprise a family of machine learning models that are well suited for implementations on near-term devices and that can potentially harness computational powers beyond what is efficiently achievable on a classical computer. However, how to best use these models -- e.g., how to control their expressivity to best balance between training accuracy and generalization performance -- is far from understood. In this paper we investigate capacity measures of two closely related QML models called explicit and implicit quantum linear classifiers (also called the quantum variational method and quantum kernel estimator) with the objective of identifying new ways to implement structural risk minimization -- i.e., how to balance between training accuracy and generalization performance. In particular, we identify that the rank and Frobenius norm of the observables used in the QML model closely control the model's capacity. Additionally, we theoretically investigate the effect that these model parameters have on the training accuracy of the QML model. Specifically, we show that there exists datasets that require a high-rank observable for correct classification, and that there exists datasets that can only be classified with a given margin using an observable of at least a certain Frobenius norm. Our results provide new options for performing structural risk minimization for QML models.

Reinforcement learning for optimization of variational quantum circuit architectures

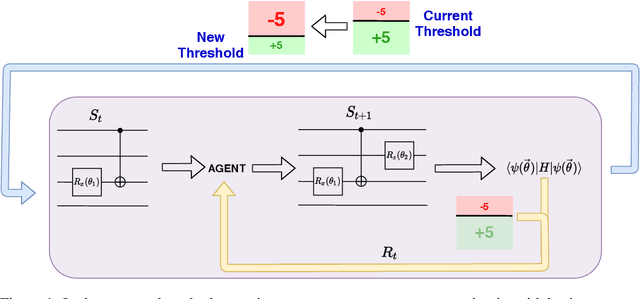
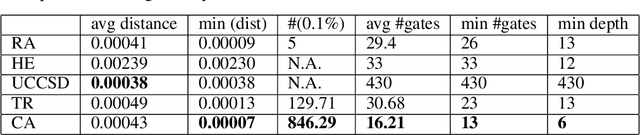
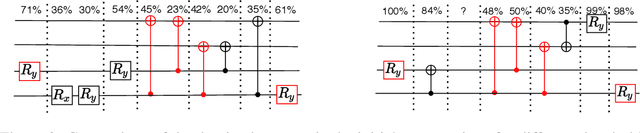
The study of Variational Quantum Eigensolvers (VQEs) has been in the spotlight in recent times as they may lead to real-world applications of near-term quantum devices. However, their performance depends on the structure of the used variational ansatz, which requires balancing the depth and expressivity of the corresponding circuit. In recent years, various methods for VQE structure optimization have been introduced but the capacities of machine learning to aid with this problem has not yet been fully investigated. In this work, we propose a reinforcement learning algorithm that autonomously explores the space of possible ans{\"a}tze, identifying economic circuits which still yield accurate ground energy estimates. The algorithm is intrinsically motivated, and it incrementally improves the accuracy of the result while minimizing the circuit depth. We showcase the performance of our algorithm on the problem of estimating the ground-state energy of lithium hydride (LiH). In this well-known benchmark problem, we achieve chemical accuracy, as well as state-of-the-art results in terms of circuit depth.

Variational quantum policies for reinforcement learning

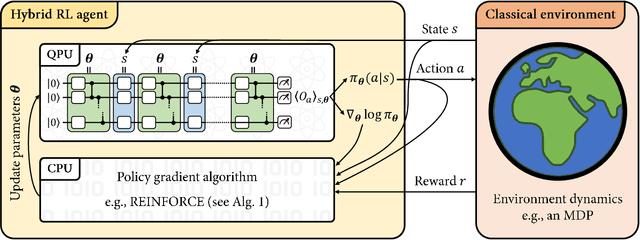
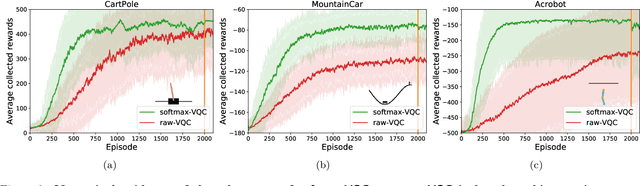
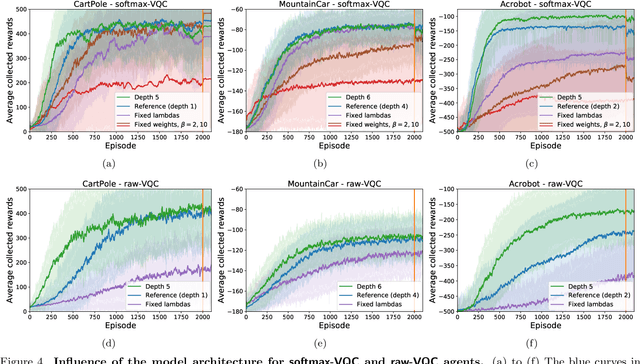
Variational quantum circuits have recently gained popularity as quantum machine learning models. While considerable effort has been invested to train them in supervised and unsupervised learning settings, relatively little attention has been given to their potential use in reinforcement learning. In this work, we leverage the understanding of quantum policy gradient algorithms in a number of ways. First, we investigate how to construct and train reinforcement learning policies based on variational quantum circuits. We propose several designs for quantum policies, provide their learning algorithms, and test their performance on classical benchmarking environments. Second, we show the existence of task environments with a provable separation in performance between quantum learning agents and any polynomial-time classical learner, conditioned on the widely-believed classical hardness of the discrete logarithm problem. We also consider more natural settings, in which we show an empirical quantum advantage of our quantum policies over standard neural-network policies. Our results constitute a first step towards establishing a practical near-term quantum advantage in a reinforcement learning setting. Additionally, we believe that some of our design choices for variational quantum policies may also be beneficial to other models based on variational quantum circuits, such as quantum classifiers and quantum regression models.