Compilation of product-formula Hamiltonian simulation via reinforcement learning

Hamiltonian simulation is believed to be one of the first tasks where quantum computers can yield a quantum advantage. One of the most popular methods of Hamiltonian simulation is Trotterization, which makes use of the approximation $e^{i\sum_jA_j}\sim \prod_je^{iA_j}$ and higher-order corrections thereto. However, this leaves open the question of the order of operations (i.e. the order of the product over $j$, which is known to affect the quality of approximation). In some cases this order is fixed by the desire to minimise the error of approximation; when it is not the case, we propose that the order can be chosen to optimize compilation to a native quantum architecture. This presents a new compilation problem -- order-agnostic quantum circuit compilation -- which we prove is NP-hard in the worst case. In lieu of an easily-computable exact solution, we turn to methods of heuristic optimization of compilation. We focus on reinforcement learning due to the sequential nature of the compilation task, comparing it to simulated annealing and Monte Carlo tree search. While two of the methods outperform a naive heuristic, reinforcement learning clearly outperforms all others, with a gain of around 12% with respect to the second-best method and of around 50% compared to the naive heuristic in terms of the gate count. We further test the ability of RL to generalize across instances of the compilation problem, and find that a single learner is able to solve entire problem families. This demonstrates the ability of machine learning techniques to provide assistance in an order-agnostic quantum compilation task.

Reinforcement learning for optimization of variational quantum circuit architectures

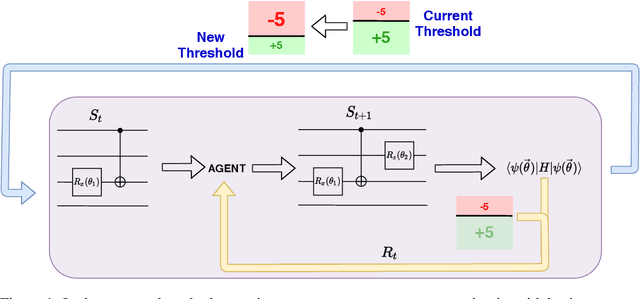
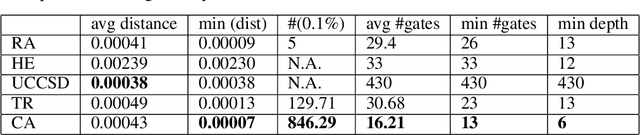
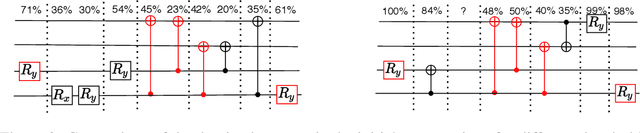
The study of Variational Quantum Eigensolvers (VQEs) has been in the spotlight in recent times as they may lead to real-world applications of near-term quantum devices. However, their performance depends on the structure of the used variational ansatz, which requires balancing the depth and expressivity of the corresponding circuit. In recent years, various methods for VQE structure optimization have been introduced but the capacities of machine learning to aid with this problem has not yet been fully investigated. In this work, we propose a reinforcement learning algorithm that autonomously explores the space of possible ans{\"a}tze, identifying economic circuits which still yield accurate ground energy estimates. The algorithm is intrinsically motivated, and it incrementally improves the accuracy of the result while minimizing the circuit depth. We showcase the performance of our algorithm on the problem of estimating the ground-state energy of lithium hydride (LiH). In this well-known benchmark problem, we achieve chemical accuracy, as well as state-of-the-art results in terms of circuit depth.