An Adaptive Re-evaluation Method for Evolution Strategy under Additive Noise

The Covariance Matrix Adaptation Evolutionary Strategy (CMA-ES) is one of the most advanced algorithms in numerical black-box optimization. For noisy objective functions, several approaches were proposed to mitigate the noise, e.g., re-evaluations of the same solution or adapting the population size. In this paper, we devise a novel method to adaptively choose the optimal re-evaluation number for function values corrupted by additive Gaussian white noise. We derive a theoretical lower bound of the expected improvement achieved in one iteration of CMA-ES, given an estimation of the noise level and the Lipschitz constant of the function's gradient. Solving for the maximum of the lower bound, we obtain a simple expression of the optimal re-evaluation number. We experimentally compare our method to the state-of-the-art noise-handling methods for CMA-ES on a set of artificial test functions across various noise levels, optimization budgets, and dimensionality. Our method demonstrates significant advantages in terms of the probability of hitting near-optimal function values.

Curriculum reinforcement learning for quantum architecture search under hardware errors

The key challenge in the noisy intermediate-scale quantum era is finding useful circuits compatible with current device limitations. Variational quantum algorithms (VQAs) offer a potential solution by fixing the circuit architecture and optimizing individual gate parameters in an external loop. However, parameter optimization can become intractable, and the overall performance of the algorithm depends heavily on the initially chosen circuit architecture. Several quantum architecture search (QAS) algorithms have been developed to design useful circuit architectures automatically. In the case of parameter optimization alone, noise effects have been observed to dramatically influence the performance of the optimizer and final outcomes, which is a key line of study. However, the effects of noise on the architecture search, which could be just as critical, are poorly understood. This work addresses this gap by introducing a curriculum-based reinforcement learning QAS (CRLQAS) algorithm designed to tackle challenges in realistic VQA deployment. The algorithm incorporates (i) a 3D architecture encoding and restrictions on environment dynamics to explore the search space of possible circuits efficiently, (ii) an episode halting scheme to steer the agent to find shorter circuits, and (iii) a novel variant of simultaneous perturbation stochastic approximation as an optimizer for faster convergence. To facilitate studies, we developed an optimized simulator for our algorithm, significantly improving computational efficiency in simulating noisy quantum circuits by employing the Pauli-transfer matrix formalism in the Pauli-Liouville basis. Numerical experiments focusing on quantum chemistry tasks demonstrate that CRLQAS outperforms existing QAS algorithms across several metrics in both noiseless and noisy environments.

Enhancing variational quantum state diagonalization using reinforcement learning techniques

The development of variational quantum algorithms is crucial for the application of NISQ computers. Such algorithms require short quantum circuits, which are more amenable to implementation on near-term hardware, and many such methods have been developed. One of particular interest is the so-called the variational diagonalization method, which constitutes an important algorithmic subroutine, and it can be used directly for working with data encoded in quantum states. In particular, it can be applied to discern the features of quantum states, such as entanglement properties of a system, or in quantum machine learning algorithms. In this work, we tackle the problem of designing a very shallow quantum circuit, required in the quantum state diagonalization task, by utilizing reinforcement learning. To achieve this, we utilize a novel encoding method that can be used to tackle the problem of circuit depth optimization using a reinforcement learning approach. We demonstrate that our approach provides a solid approximation to the diagonalization task while using a small number of gates. The circuits proposed by the reinforcement learning methods are shallower than the standard variational quantum state diagonalization algorithm, and thus can be used in situations where the depth of quantum circuits is limited by the hardware capabilities.

Reinforcement Learning Assisted Recursive QAOA

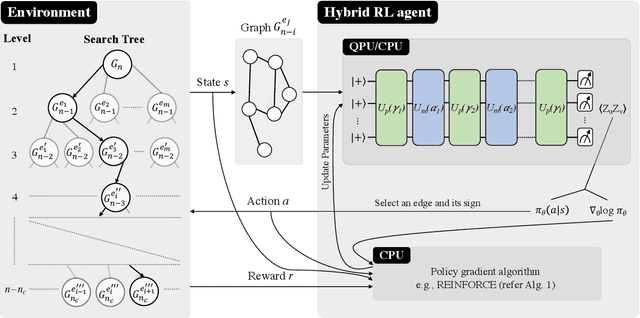
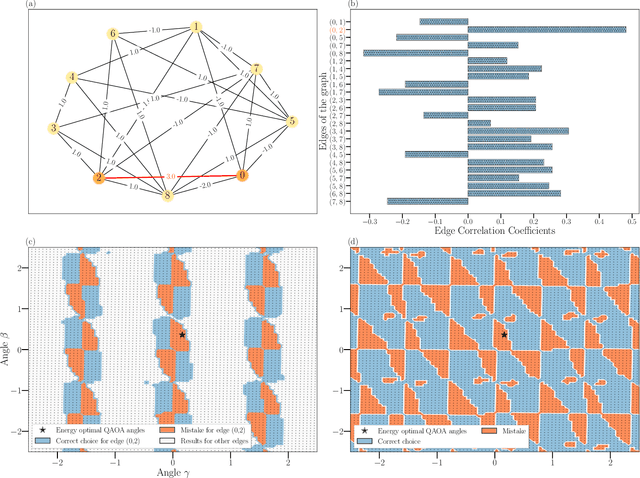
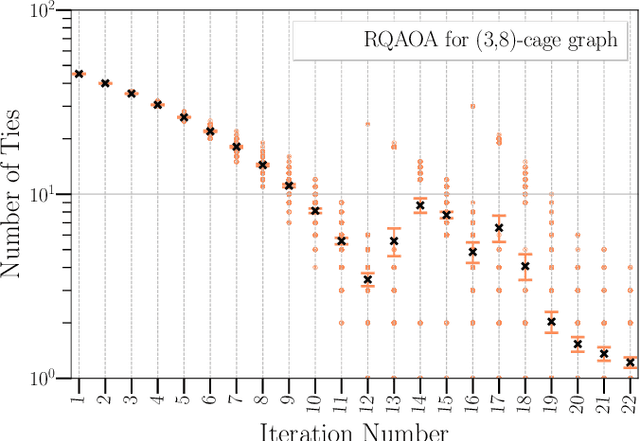
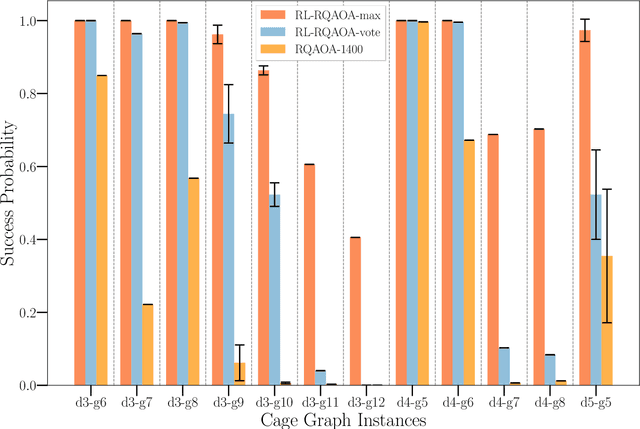
Variational quantum algorithms such as the Quantum Approximation Optimization Algorithm (QAOA) in recent years have gained popularity as they provide the hope of using NISQ devices to tackle hard combinatorial optimization problems. It is, however, known that at low depth, certain locality constraints of QAOA limit its performance. To go beyond these limitations, a non-local variant of QAOA, namely recursive QAOA (RQAOA), was proposed to improve the quality of approximate solutions. The RQAOA has been studied comparatively less than QAOA, and it is less understood, for instance, for what family of instances it may fail to provide high quality solutions. However, as we are tackling $\mathsf{NP}$-hard problems (specifically, the Ising spin model), it is expected that RQAOA does fail, raising the question of designing even better quantum algorithms for combinatorial optimization. In this spirit, we identify and analyze cases where RQAOA fails and, based on this, propose a reinforcement learning enhanced RQAOA variant (RL-RQAOA) that improves upon RQAOA. We show that the performance of RL-RQAOA improves over RQAOA: RL-RQAOA is strictly better on these identified instances where RQAOA underperforms, and is similarly performing on instances where RQAOA is near-optimal. Our work exemplifies the potentially beneficial synergy between reinforcement learning and quantum (inspired) optimization in the design of new, even better heuristics for hard problems.