Implicit Regularization for Optimal Sparse Recovery

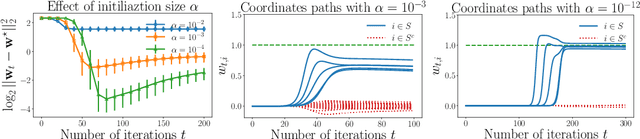
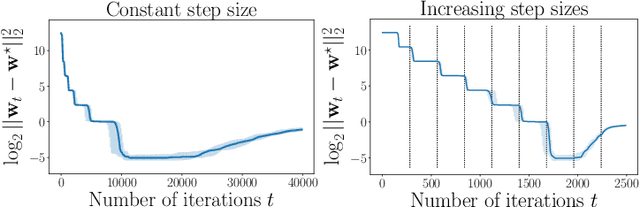
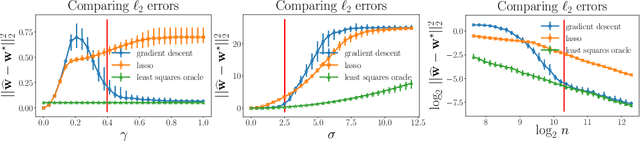
We investigate implicit regularization schemes for gradient descent methods applied to unpenalized least squares regression to solve the problem of reconstructing a sparse signal from an underdetermined system of linear measurements under the restricted isometry assumption. For a given parametrization yielding a non-convex optimization problem, we show that prescribed choices of initialization, step size and stopping time yield a statistically and computationally optimal algorithm that achieves the minimax rate with the same cost required to read the data up to poly-logarithmic factors. Beyond minimax optimality, we show that our algorithm adapts to instance difficulty and yields a dimension-independent rate when the signal-to-noise ratio is high enough. Key to the computational efficiency of our method is an increasing step size scheme that adapts to refined estimates of the true solution. We validate our findings with numerical experiments and compare our algorithm against explicit $\ell_{1}$ penalization. Going from hard instances to easy ones, our algorithm is seen to undergo a phase transition, eventually matching least squares with an oracle knowledge of the true support.

Adaptive Reduced Rank Regression

Low rank regression has proven to be useful in a wide range of forecasting problems. However, in settings with a low signal-to-noise ratio, it is known to suffer from severe overfitting. This paper studies the reduced rank regression problem and presents algorithms with provable generalization guarantees. We use adaptive hard rank-thresholding in two different parts of the data analysis pipeline. First, we consider a low rank projection of the data to eliminate the components that are most likely to be noisy. Second, we perform a standard multivariate linear regression estimator on the data obtained in the first step, and subsequently consider a low-rank projection of the obtained regression matrix. Both thresholding is performed in a data-driven manner and is required to prevent severe overfitting as our lower bounds show. Experimental results show that our approach either outperforms or is competitive with existing baselines.

Decentralized Cooperative Stochastic Multi-armed Bandits

We study a decentralized cooperative stochastic multi-armed bandit problem with $K$ arms on a network of $N$ agents. In our model, the reward distribution of each arm is agent-independent. Each agent chooses iteratively one arm to play and then communicates to her neighbors. The aim is to minimize the total network regret. We design a fully decentralized algorithm that uses a running consensus procedure to compute, with some delay, accurate estimations of the average of rewards obtained by all the agents for each arm, and then uses an upper confidence bound algorithm that accounts for the delay and error of the estimations. We analyze the algorithm and up to a constant our regret bounds are better for all networks than other algorithms designed to solve the same problem. For some graphs, our regret bounds are significantly better.

Statistical Windows in Testing for the Initial Distribution of a Reversible Markov Chain

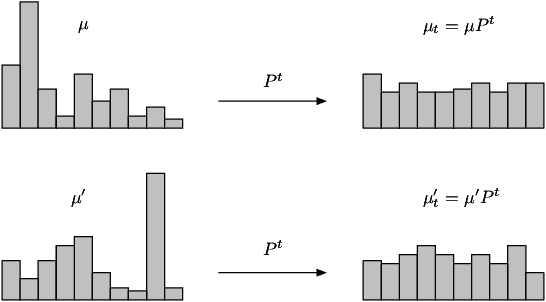
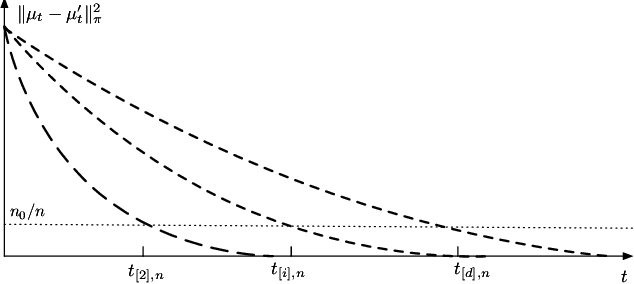
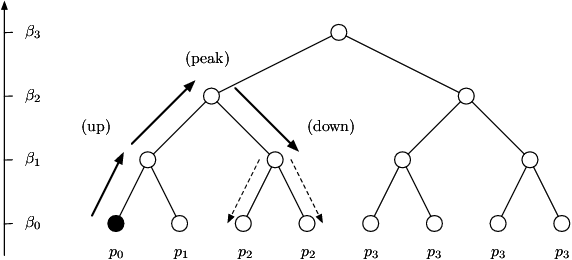
We study the problem of hypothesis testing between two discrete distributions, where we only have access to samples after the action of a known reversible Markov chain, playing the role of noise. We derive instance-dependent minimax rates for the sample complexity of this problem, and show how its dependence in time is related to the spectral properties of the Markov chain. We show that there exists a wide statistical window, in terms of sample complexity for hypothesis testing between different pairs of initial distributions. We illustrate these results in several concrete examples.

Intriguing Properties of Learned Representations

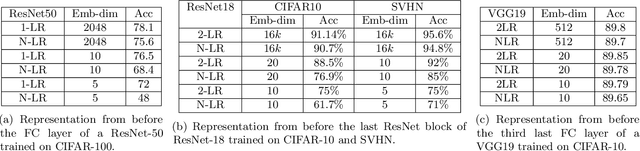
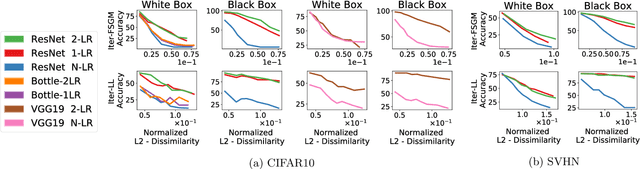
A key feature of neural networks, particularly deep convolutional neural networks, is their ability to "learn" useful representations from data. The very last layer of a neural network is then simply a linear model trained on these "learned" representations. Despite their numerous applications in other tasks such as classification, retrieval, clustering etc., a.k.a. transfer learning, not much work has been published that investigates the structure of these representations or indeed whether structure can be imposed on them during the training process. In this paper, we study the effective dimensionality of the learned representations by models that have proved highly successful for image classification. We focus on ResNet-18, ResNet-50 and VGG-19 and observe that when trained on CIFAR10 or CIFAR100, the learned representations exhibit a fairly low rank structure. We propose a modification to the training procedure, which further encourages low rank structure on learned activations. Empirically, we show that this has implications for robustness to adversarial examples and compression.

TAPAS: Tricks to Accelerate Prediction As a Service

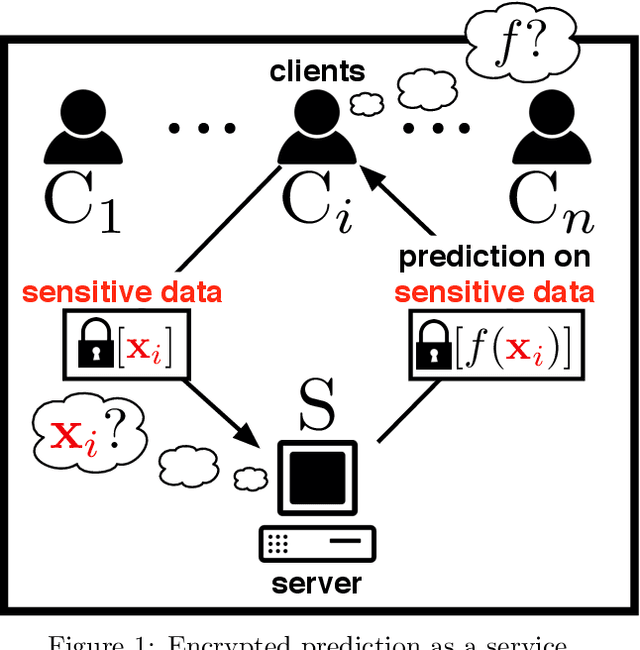
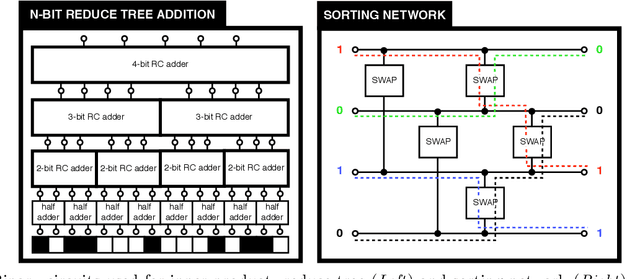
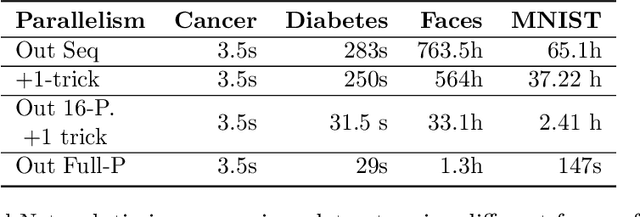
Machine learning methods are widely used for a variety of prediction problems. \emph{Prediction as a service} is a paradigm in which service providers with technological expertise and computational resources may perform predictions for clients. However, data privacy severely restricts the applicability of such services, unless measures to keep client data private (even from the service provider) are designed. Equally important is to minimize the amount of computation and communication required between client and server. Fully homomorphic encryption offers a possible way out, whereby clients may encrypt their data, and on which the server may perform arithmetic computations. The main drawback of using fully homomorphic encryption is the amount of time required to evaluate large machine learning models on encrypted data. We combine ideas from the machine learning literature, particularly work on binarization and sparsification of neural networks, together with algorithmic tools to speed-up and parallelize computation using encrypted data.

Learning DNFs under product distributions via μ-biased quantum Fourier sampling

We show that DNF formulae can be quantum PAC-learned in polynomial time under product distributions using a quantum example oracle. The best classical algorithm (without access to membership queries) runs in superpolynomial time. Our result extends the work by Bshouty and Jackson (1998) that proved that DNF formulae are efficiently learnable under the uniform distribution using a quantum example oracle. Our proof is based on a new quantum algorithm that efficiently samples the coefficients of a {\mu}-biased Fourier transform.

From which world is your graph?

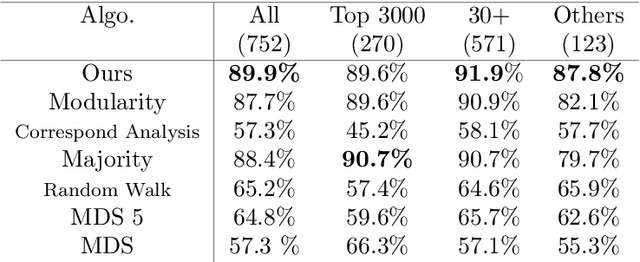
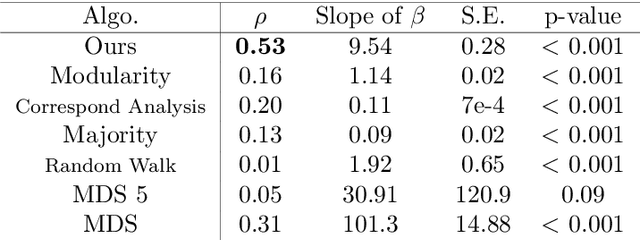
Discovering statistical structure from links is a fundamental problem in the analysis of social networks. Choosing a misspecified model, or equivalently, an incorrect inference algorithm will result in an invalid analysis or even falsely uncover patterns that are in fact artifacts of the model. This work focuses on unifying two of the most widely used link-formation models: the stochastic blockmodel (SBM) and the small world (or latent space) model (SWM). Integrating techniques from kernel learning, spectral graph theory, and nonlinear dimensionality reduction, we develop the first statistically sound polynomial-time algorithm to discover latent patterns in sparse graphs for both models. When the network comes from an SBM, the algorithm outputs a block structure. When it is from an SWM, the algorithm outputs estimates of each node's latent position.

Hierarchical Clustering: Objective Functions and Algorithms

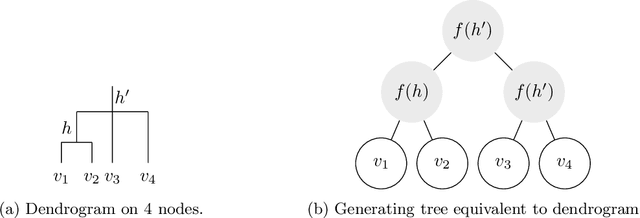
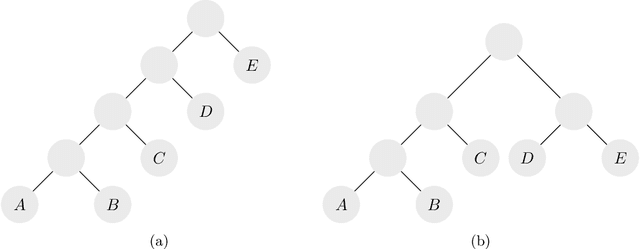
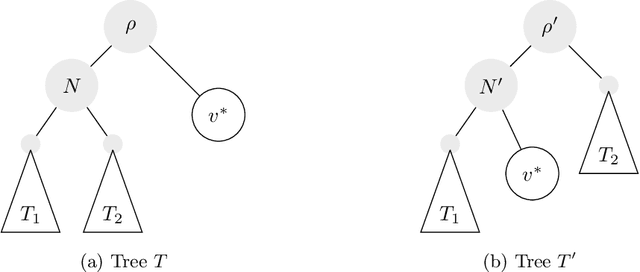
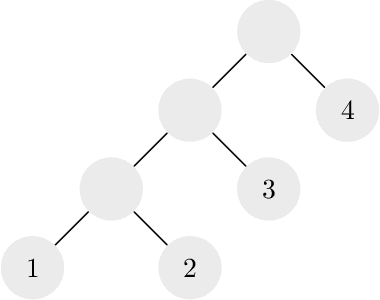
Hierarchical clustering is a recursive partitioning of a dataset into clusters at an increasingly finer granularity. Motivated by the fact that most work on hierarchical clustering was based on providing algorithms, rather than optimizing a specific objective, Dasgupta framed similarity-based hierarchical clustering as a combinatorial optimization problem, where a `good' hierarchical clustering is one that minimizes some cost function. He showed that this cost function has certain desirable properties. We take an axiomatic approach to defining `good' objective functions for both similarity and dissimilarity-based hierarchical clustering. We characterize a set of "admissible" objective functions (that includes Dasgupta's one) that have the property that when the input admits a `natural' hierarchical clustering, it has an optimal value. Equipped with a suitable objective function, we analyze the performance of practical algorithms, as well as develop better algorithms. For similarity-based hierarchical clustering, Dasgupta showed that the divisive sparsest-cut approach achieves an $O(\log^{3/2} n)$-approximation. We give a refined analysis of the algorithm and show that it in fact achieves an $O(\sqrt{\log n})$-approx. (Charikar and Chatziafratis independently proved that it is a $O(\sqrt{\log n})$-approx.). This improves upon the LP-based $O(\log n)$-approx. of Roy and Pokutta. For dissimilarity-based hierarchical clustering, we show that the classic average-linkage algorithm gives a factor 2 approx., and provide a simple and better algorithm that gives a factor 3/2 approx.. Finally, we consider `beyond-worst-case' scenario through a generalisation of the stochastic block model for hierarchical clustering. We show that Dasgupta's cost function has desirable properties for these inputs and we provide a simple 1 + o(1)-approximation in this setting.

Reliably Learning the ReLU in Polynomial Time

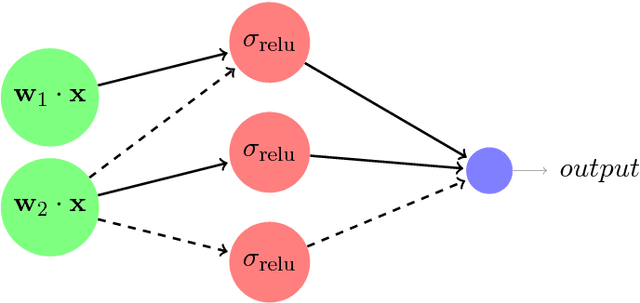
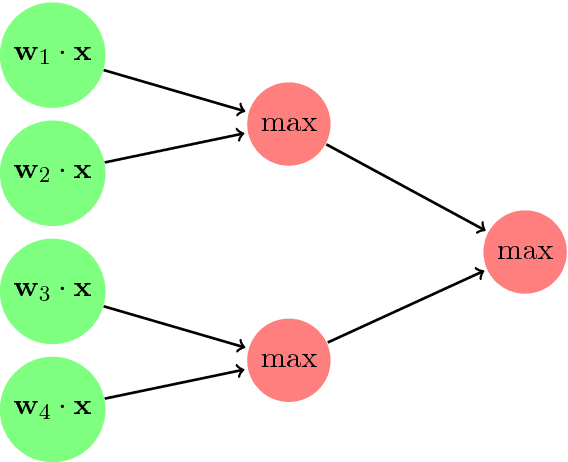
We give the first dimension-efficient algorithms for learning Rectified Linear Units (ReLUs), which are functions of the form $\mathbf{x} \mapsto \max(0, \mathbf{w} \cdot \mathbf{x})$ with $\mathbf{w} \in \mathbb{S}^{n-1}$. Our algorithm works in the challenging Reliable Agnostic learning model of Kalai, Kanade, and Mansour (2009) where the learner is given access to a distribution $\cal{D}$ on labeled examples but the labeling may be arbitrary. We construct a hypothesis that simultaneously minimizes the false-positive rate and the loss on inputs given positive labels by $\cal{D}$, for any convex, bounded, and Lipschitz loss function. The algorithm runs in polynomial-time (in $n$) with respect to any distribution on $\mathbb{S}^{n-1}$ (the unit sphere in $n$ dimensions) and for any error parameter $\epsilon = \Omega(1/\log n)$ (this yields a PTAS for a question raised by F. Bach on the complexity of maximizing ReLUs). These results are in contrast to known efficient algorithms for reliably learning linear threshold functions, where $\epsilon$ must be $\Omega(1)$ and strong assumptions are required on the marginal distribution. We can compose our results to obtain the first set of efficient algorithms for learning constant-depth networks of ReLUs. Our techniques combine kernel methods and polynomial approximations with a "dual-loss" approach to convex programming. As a byproduct we obtain a number of applications including the first set of efficient algorithms for "convex piecewise-linear fitting" and the first efficient algorithms for noisy polynomial reconstruction of low-weight polynomials on the unit sphere.