A Unified Framework for Provably Efficient Algorithms to Estimate Shapley Values

Shapley values have emerged as a critical tool for explaining which features impact the decisions made by machine learning models. However, computing exact Shapley values is difficult, generally requiring an exponential (in the feature dimension) number of model evaluations. To address this, many model-agnostic randomized estimators have been developed, the most influential and widely used being the KernelSHAP method (Lundberg & Lee, 2017). While related estimators such as unbiased KernelSHAP (Covert & Lee, 2021) and LeverageSHAP (Musco & Witter, 2025) are known to satisfy theoretical guarantees, bounds for KernelSHAP have remained elusive. We describe a broad and unified framework that encompasses KernelSHAP and related estimators constructed using both with and without replacement sampling strategies. We then prove strong non-asymptotic theoretical guarantees that apply to all estimators from our framework. This provides, to the best of our knowledge, the first theoretical guarantees for KernelSHAP and sheds further light on tradeoffs between existing estimators. Through comprehensive benchmarking on small and medium dimensional datasets for Decision-Tree models, we validate our approach against exact Shapley values, consistently achieving low mean squared error with modest sample sizes. Furthermore, we make specific implementation improvements to enable scalability of our methods to high-dimensional datasets. Our methods, tested on datasets such MNIST and CIFAR10, provide consistently better results compared to the KernelSHAP library.

Provably faster randomized and quantum algorithms for k-means clustering via uniform sampling

The $k$-means algorithm (Lloyd's algorithm) is a widely used method for clustering unlabeled data. A key bottleneck of the $k$-means algorithm is that each iteration requires time linear in the number of data points, which can be expensive in big data applications. This was improved in recent works proposing quantum and quantum-inspired classical algorithms to approximate the $k$-means algorithm locally, in time depending only logarithmically on the number of data points (along with data dependent parameters) [$q$-means: A quantum algorithm for unsupervised machine learning; Kerenidis, Landman, Luongo, and Prakash, NeurIPS 2019; Do you know what $q$-means?, Doriguello, Luongo, Tang]. In this work, we describe a simple randomized mini-batch $k$-means algorithm and a quantum algorithm inspired by the classical algorithm. We prove worse-case guarantees that significantly improve upon the bounds for previous algorithms. Our improvements are due to a careful use of uniform sampling, which preserves certain symmetries of the $k$-means problem that are not preserved in previous algorithms that use data norm-based sampling.

Large-scale Outdoor Cell-free mMIMO Channel Measurement in an Urban Scenario at 3.5 GHz

The design of cell-free massive MIMO (CF-mMIMO) systems requires accurate, measurement-based channel models. This paper provides the first results from the by far most extensive outdoor measurement campaign for CF-mMIMO channels in an urban environment. We measured impulse responses between over 20,000 potential access point (AP) locations and 80 user equipments (UEs) at 3.5 GHz with 350 MHz bandwidth (BW). Measurements use a "virtual array" approach at the AP and a hybrid switched/virtual approach at the UE. This paper describes the sounder design, measurement environment, data processing, and sample results, particularly the evolution of the power-delay profiles (PDPs) as a function of the AP locations, and its relation to the propagation environment.

On the fast convergence of minibatch heavy ball momentum

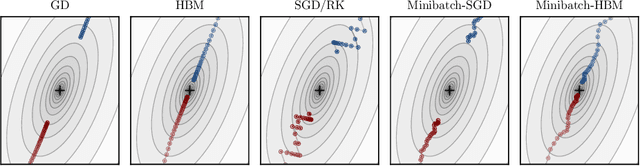
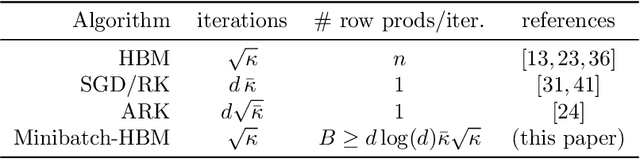
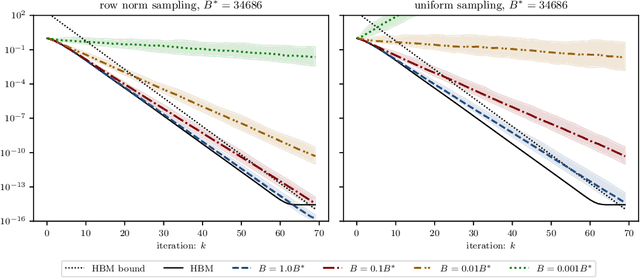
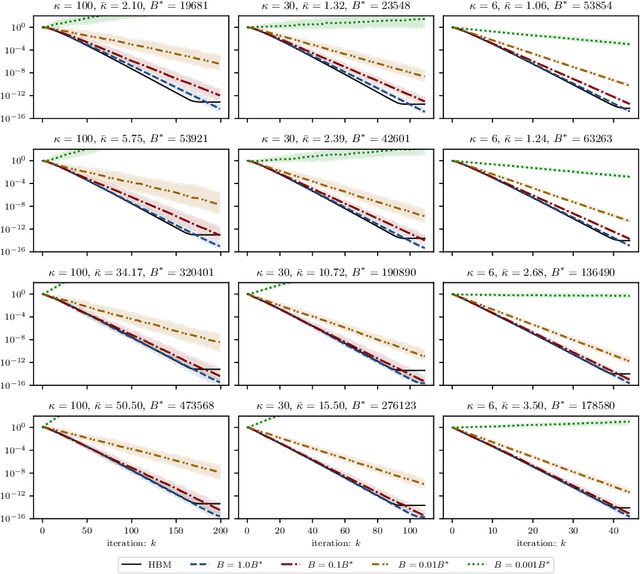
Simple stochastic momentum methods are widely used in machine learning optimization, but their good practical performance is at odds with an absence of theoretical guarantees of acceleration in the literature. In this work, we aim to close the gap between theory and practice by showing that stochastic heavy ball momentum, which can be interpreted as a randomized Kaczmarz algorithm with momentum, retains the fast linear rate of (deterministic) heavy ball momentum on quadratic optimization problems, at least when minibatching with a sufficiently large batch size is used. The analysis relies on carefully decomposing the momentum transition matrix, and using new spectral norm concentration bounds for products of independent random matrices. We provide numerical experiments to demonstrate that our bounds are reasonably sharp.