On Explore-Then-Commit Strategies

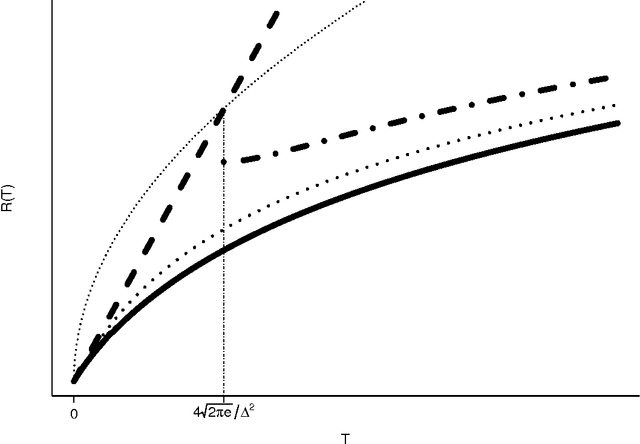
We study the problem of minimising regret in two-armed bandit problems with Gaussian rewards. Our objective is to use this simple setting to illustrate that strategies based on an exploration phase (up to a stopping time) followed by exploitation are necessarily suboptimal. The results hold regardless of whether or not the difference in means between the two arms is known. Besides the main message, we also refine existing deviation inequalities, which allow us to design fully sequential strategies with finite-time regret guarantees that are (a) asymptotically optimal as the horizon grows and (b) order-optimal in the minimax sense. Furthermore we provide empirical evidence that the theory also holds in practice and discuss extensions to non-gaussian and multiple-armed case.

The End of Optimism? An Asymptotic Analysis of Finite-Armed Linear Bandits

Stochastic linear bandits are a natural and simple generalisation of finite-armed bandits with numerous practical applications. Current approaches focus on generalising existing techniques for finite-armed bandits, notably the optimism principle and Thompson sampling. While prior work has mostly been in the worst-case setting, we analyse the asymptotic instance-dependent regret and show matching upper and lower bounds on what is achievable. Surprisingly, our results show that no algorithm based on optimism or Thompson sampling will ever achieve the optimal rate, and indeed, can be arbitrarily far from optimal, even in very simple cases. This is a disturbing result because these techniques are standard tools that are widely used for sequential optimisation. For example, for generalised linear bandits and reinforcement learning.

Free Lunch for Optimisation under the Universal Distribution

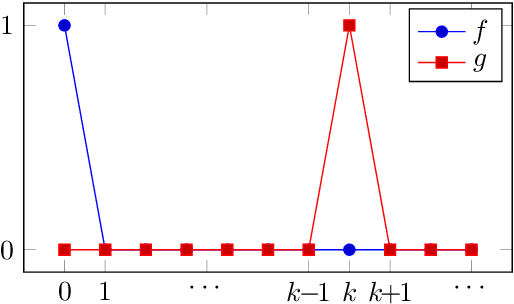
Function optimisation is a major challenge in computer science. The No Free Lunch theorems state that if all functions with the same histogram are assumed to be equally probable then no algorithm outperforms any other in expectation. We argue against the uniform assumption and suggest a universal prior exists for which there is a free lunch, but where no particular class of functions is favoured over another. We also prove upper and lower bounds on the size of the free lunch.

Causal Bandits: Learning Good Interventions via Causal Inference

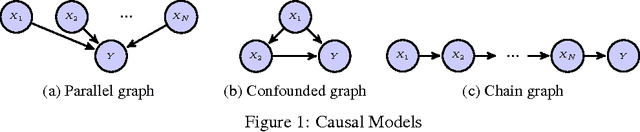
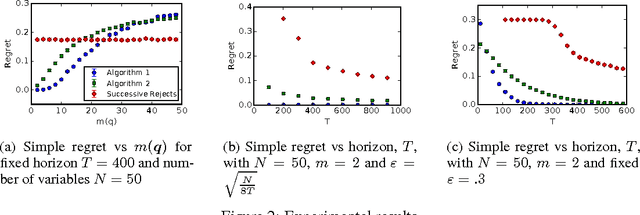
We study the problem of using causal models to improve the rate at which good interventions can be learned online in a stochastic environment. Our formalism combines multi-arm bandits and causal inference to model a novel type of bandit feedback that is not exploited by existing approaches. We propose a new algorithm that exploits the causal feedback and prove a bound on its simple regret that is strictly better (in all quantities) than algorithms that do not use the additional causal information.

Thompson Sampling is Asymptotically Optimal in General Environments

We discuss a variant of Thompson sampling for nonparametric reinforcement learning in a countable classes of general stochastic environments. These environments can be non-Markov, non-ergodic, and partially observable. We show that Thompson sampling learns the environment class in the sense that (1) asymptotically its value converges to the optimal value in mean and (2) given a recoverability assumption regret is sublinear.

Regret Analysis of the Finite-Horizon Gittins Index Strategy for Multi-Armed Bandits

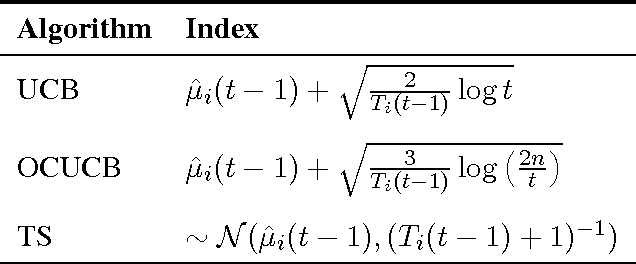
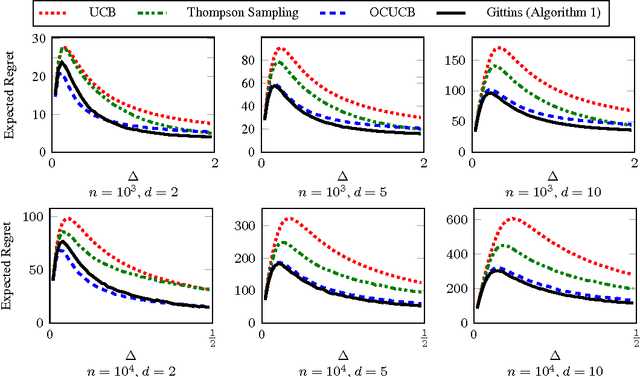
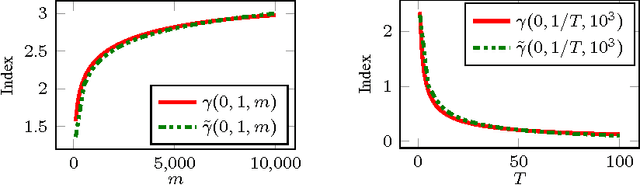
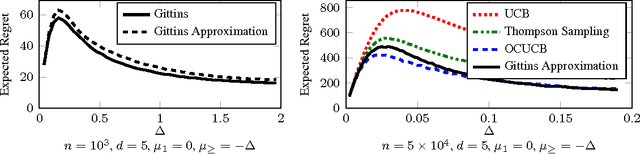
I analyse the frequentist regret of the famous Gittins index strategy for multi-armed bandits with Gaussian noise and a finite horizon. Remarkably it turns out that this approach leads to finite-time regret guarantees comparable to those available for the popular UCB algorithm. Along the way I derive finite-time bounds on the Gittins index that are asymptotically exact and may be of independent interest. I also discuss some computational issues and present experimental results suggesting that a particular version of the Gittins index strategy is a modest improvement on existing algorithms with finite-time regret guarantees such as UCB and Thompson sampling.

Regret Analysis of the Anytime Optimally Confident UCB Algorithm

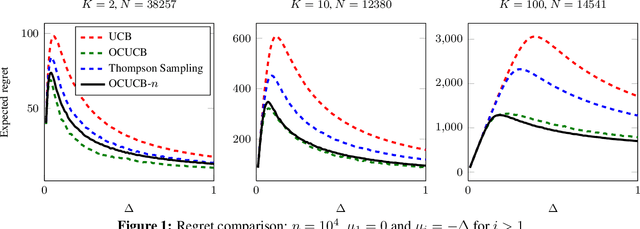
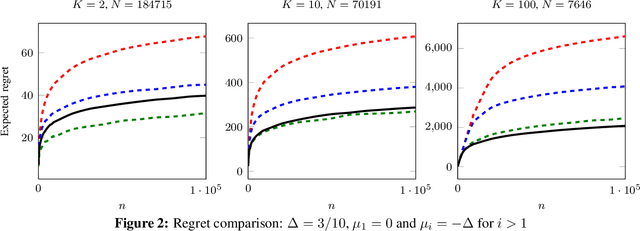
I introduce and analyse an anytime version of the Optimally Confident UCB (OCUCB) algorithm designed for minimising the cumulative regret in finite-armed stochastic bandits with subgaussian noise. The new algorithm is simple, intuitive (in hindsight) and comes with the strongest finite-time regret guarantees for a horizon-free algorithm so far. I also show a finite-time lower bound that nearly matches the upper bound.

Optimally Confident UCB: Improved Regret for Finite-Armed Bandits

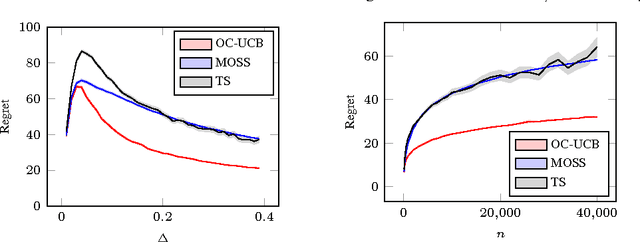
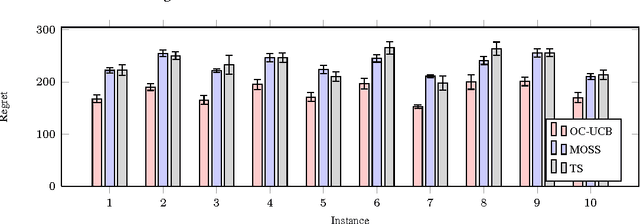
I present the first algorithm for stochastic finite-armed bandits that simultaneously enjoys order-optimal problem-dependent regret and worst-case regret. Besides the theoretical results, the new algorithm is simple, efficient and empirically superb. The approach is based on UCB, but with a carefully chosen confidence parameter that optimally balances the risk of failing confidence intervals against the cost of excessive optimism.

Conservative Bandits

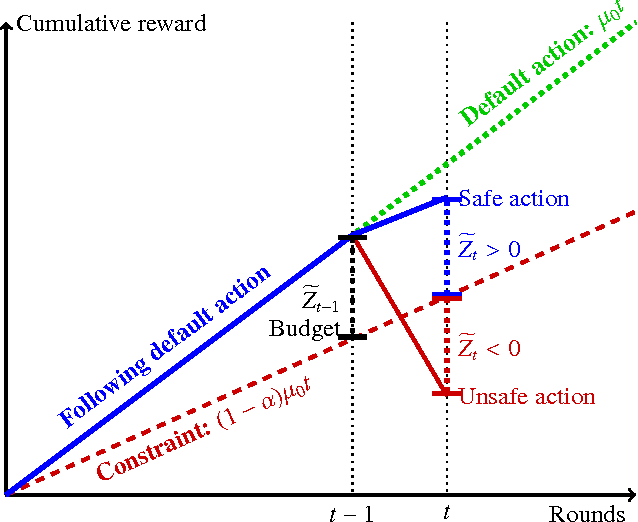
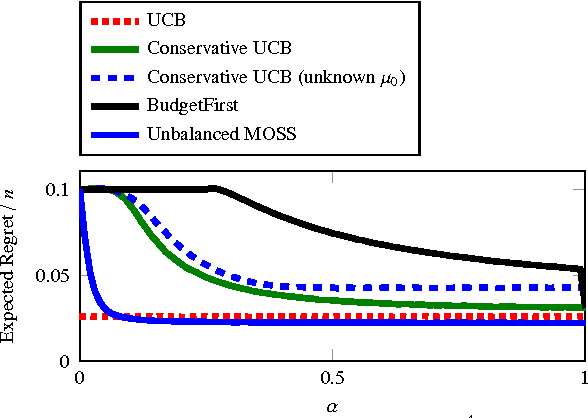
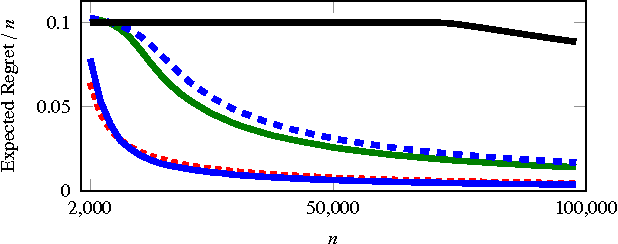
We study a novel multi-armed bandit problem that models the challenge faced by a company wishing to explore new strategies to maximize revenue whilst simultaneously maintaining their revenue above a fixed baseline, uniformly over time. While previous work addressed the problem under the weaker requirement of maintaining the revenue constraint only at a given fixed time in the future, the algorithms previously proposed are unsuitable due to their design under the more stringent constraints. We consider both the stochastic and the adversarial settings, where we propose, natural, yet novel strategies and analyze the price for maintaining the constraints. Amongst other things, we prove both high probability and expectation bounds on the regret, while we also consider both the problem of maintaining the constraints with high probability or expectation. For the adversarial setting the price of maintaining the constraint appears to be higher, at least for the algorithm considered. A lower bound is given showing that the algorithm for the stochastic setting is almost optimal. Empirical results obtained in synthetic environments complement our theoretical findings.

The Pareto Regret Frontier for Bandits

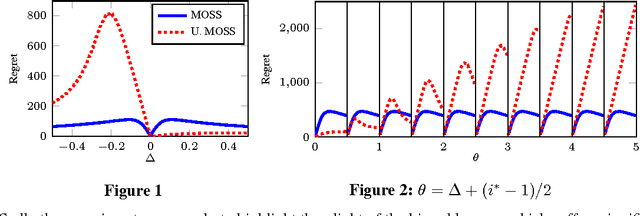
Given a multi-armed bandit problem it may be desirable to achieve a smaller-than-usual worst-case regret for some special actions. I show that the price for such unbalanced worst-case regret guarantees is rather high. Specifically, if an algorithm enjoys a worst-case regret of B with respect to some action, then there must exist another action for which the worst-case regret is at least {\Omega}(nK/B), where n is the horizon and K the number of actions. I also give upper bounds in both the stochastic and adversarial settings showing that this result cannot be improved. For the stochastic case the pareto regret frontier is characterised exactly up to constant factors.