Adversarial Dueling Bandits

We introduce the problem of regret minimization in Adversarial Dueling Bandits. As in classic Dueling Bandits, the learner has to repeatedly choose a pair of items and observe only a relative binary `win-loss' feedback for this pair, but here this feedback is generated from an arbitrary preference matrix, possibly chosen adversarially. Our main result is an algorithm whose $T$-round regret compared to the \emph{Borda-winner} from a set of $K$ items is $\tilde{O}(K^{1/3}T^{2/3})$, as well as a matching $\Omega(K^{1/3}T^{2/3})$ lower bound. We also prove a similar high probability regret bound. We further consider a simpler \emph{fixed-gap} adversarial setup, which bridges between two extreme preference feedback models for dueling bandits: stationary preferences and an arbitrary sequence of preferences. For the fixed-gap adversarial setup we give an $\smash{ \tilde{O}((K/\Delta^2)\log{T}) }$ regret algorithm, where $\Delta$ is the gap in Borda scores between the best item and all other items, and show a lower bound of $\Omega(K/\Delta^2)$ indicating that our dependence on the main problem parameters $K$ and $\Delta$ is tight (up to logarithmic factors).

Stochastic Optimization with Laggard Data Pipelines

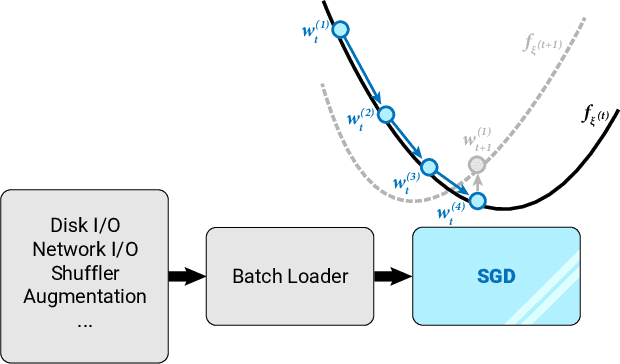
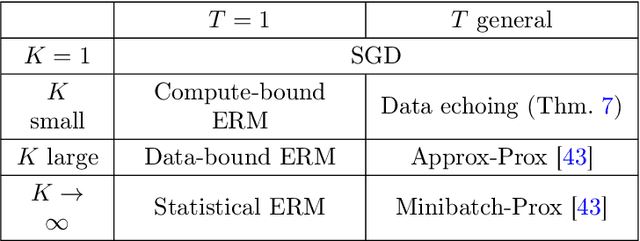
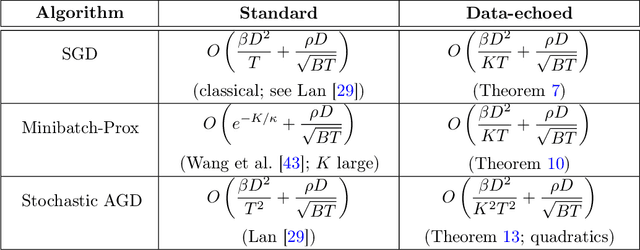
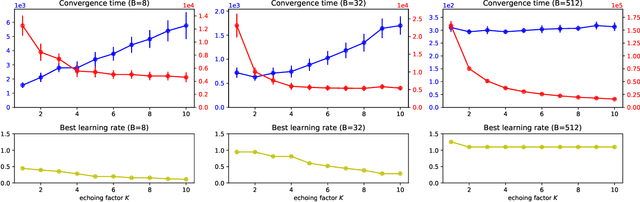
State-of-the-art optimization is steadily shifting towards massively parallel pipelines with extremely large batch sizes. As a consequence, CPU-bound preprocessing and disk/memory/network operations have emerged as new performance bottlenecks, as opposed to hardware-accelerated gradient computations. In this regime, a recently proposed approach is data echoing (Choi et al., 2019), which takes repeated gradient steps on the same batch while waiting for fresh data to arrive from upstream. We provide the first convergence analyses of "data-echoed" extensions of common optimization methods, showing that they exhibit provable improvements over their synchronous counterparts. Specifically, we show that in convex optimization with stochastic minibatches, data echoing affords speedups on the curvature-dominated part of the convergence rate, while maintaining the optimal statistical rate.

Holdout SGD: Byzantine Tolerant Federated Learning

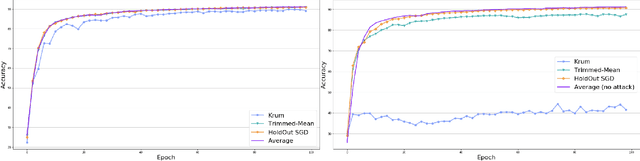
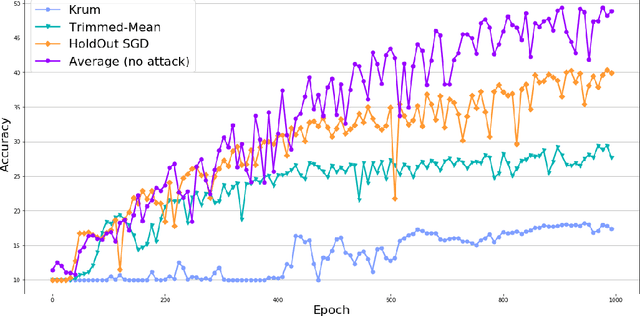
This work presents a new distributed Byzantine tolerant federated learning algorithm, HoldOut SGD, for Stochastic Gradient Descent (SGD) optimization. HoldOut SGD uses the well known machine learning technique of holdout estimation, in a distributed fashion, in order to select parameter updates that are likely to lead to models with low loss values. This makes it more effective at discarding Byzantine workers inputs than existing methods that eliminate outliers in the parameter-space of the learned model. HoldOut SGD first randomly selects a set of workers that use their private data in order to propose gradient updates. Next, a voting committee of workers is randomly selected, and each voter uses its private data as holdout data, in order to select the best proposals via a voting scheme. We propose two possible mechanisms for the coordination of workers in the distributed computation of HoldOut SGD. The first uses a truthful central server and corresponds to the typical setting of current federated learning. The second is fully distributed and requires no central server, paving the way to fully decentralized federated learning. The fully distributed version implements HoldOut SGD via ideas from the blockchain domain, and specifically the Algorand committee selection and consensus processes. We provide formal guarantees for the HoldOut SGD process in terms of its convergence to the optimal model, and its level of resilience to the fraction of Byzantine workers. Empirical evaluation shows that HoldOut SGD is Byzantine-resilient and efficiently converges to an effectual model for deep-learning tasks, as long as the total number of participating workers is large and the fraction of Byzantine workers is less than half (<1/3 for the fully distributed variant).

Bandit Linear Control

We consider the problem of controlling a known linear dynamical system under stochastic noise, adversarially chosen costs, and bandit feedback. Unlike the full feedback setting where the entire cost function is revealed after each decision, here only the cost incurred by the learner is observed. We present a new and efficient algorithm that, for strongly convex and smooth costs, obtains regret that grows with the square root of the time horizon $T$. We also give extensions of this result to general convex, possibly non-smooth costs, and to non-stochastic system noise. A key component of our algorithm is a new technique for addressing bandit optimization of loss functions with memory.

Private Stochastic Convex Optimization: Optimal Rates in Linear Time

We study differentially private (DP) algorithms for stochastic convex optimization: the problem of minimizing the population loss given i.i.d. samples from a distribution over convex loss functions. A recent work of Bassily et al. (2019) has established the optimal bound on the excess population loss achievable given $n$ samples. Unfortunately, their algorithm achieving this bound is relatively inefficient: it requires $O(\min\{n^{3/2}, n^{5/2}/d\})$ gradient computations, where $d$ is the dimension of the optimization problem. We describe two new techniques for deriving DP convex optimization algorithms both achieving the optimal bound on excess loss and using $O(\min\{n, n^2/d\})$ gradient computations. In particular, the algorithms match the running time of the optimal non-private algorithms. The first approach relies on the use of variable batch sizes and is analyzed using the privacy amplification by iteration technique of Feldman et al. (2018). The second approach is based on a general reduction to the problem of localizing an approximately optimal solution with differential privacy. Such localization, in turn, can be achieved using existing (non-private) uniformly stable optimization algorithms. As in the earlier work, our algorithms require a mild smoothness assumption. We also give a linear-time algorithm achieving the optimal bound on the excess loss for the strongly convex case, as well as a faster algorithm for the non-smooth case.

Can Implicit Bias Explain Generalization? Stochastic Convex Optimization as a Case Study

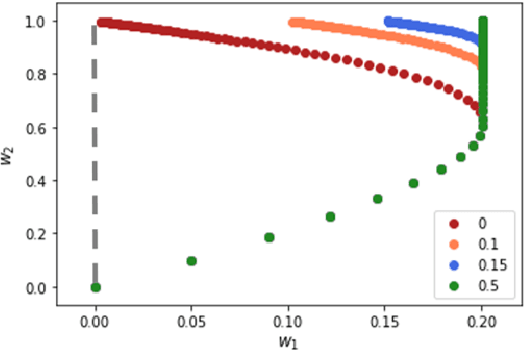
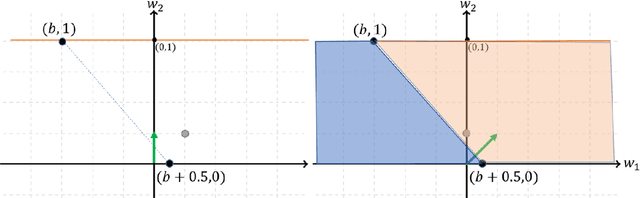
The notion of implicit bias, or implicit regularization, has been suggested as a means to explain the surprising generalization ability of modern-days overparameterized learning algorithms. This notion refers to the tendency of the optimization algorithm towards a certain structured solution that often generalizes well. Recently, several papers have studied implicit regularization and were able to identify this phenomenon in various scenarios. We revisit this paradigm in arguably the simplest non-trivial setup, and study the implicit bias of Stochastic Gradient Descent (SGD) in the context of Stochastic Convex Optimization. As a first step, we provide a simple construction that rules out the existence of a \emph{distribution-independent} implicit regularizer that governs the generalization ability of SGD. We then demonstrate a learning problem that rules out a very general class of \emph{distribution-dependent} implicit regularizers from explaining generalization, which includes strongly convex regularizers as well as non-degenerate norm-based regularizations. Certain aspects of our constructions point out to significant difficulties in providing a comprehensive explanation of an algorithm's generalization performance by solely arguing about its implicit regularization properties.

Disentangling Adaptive Gradient Methods from Learning Rates

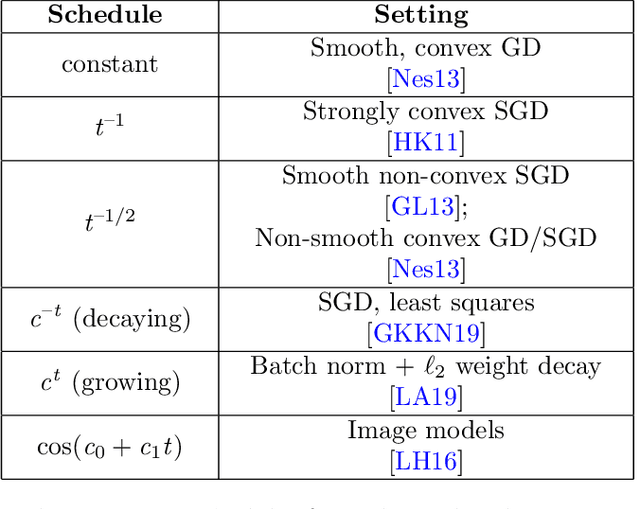
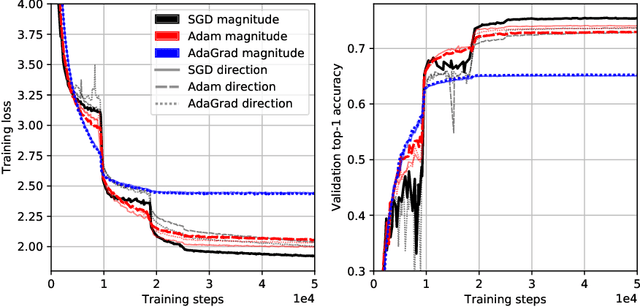
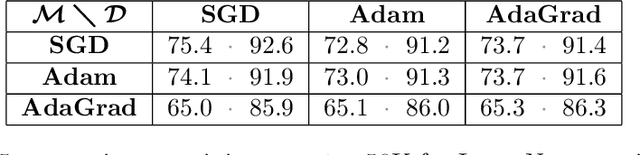
We investigate several confounding factors in the evaluation of optimization algorithms for deep learning. Primarily, we take a deeper look at how adaptive gradient methods interact with the learning rate schedule, a notoriously difficult-to-tune hyperparameter which has dramatic effects on the convergence and generalization of neural network training. We introduce a "grafting" experiment which decouples an update's magnitude from its direction, finding that many existing beliefs in the literature may have arisen from insufficient isolation of the implicit schedule of step sizes. Alongside this contribution, we present some empirical and theoretical retrospectives on the generalization of adaptive gradient methods, aimed at bringing more clarity to this space.

Prediction with Corrupted Expert Advice

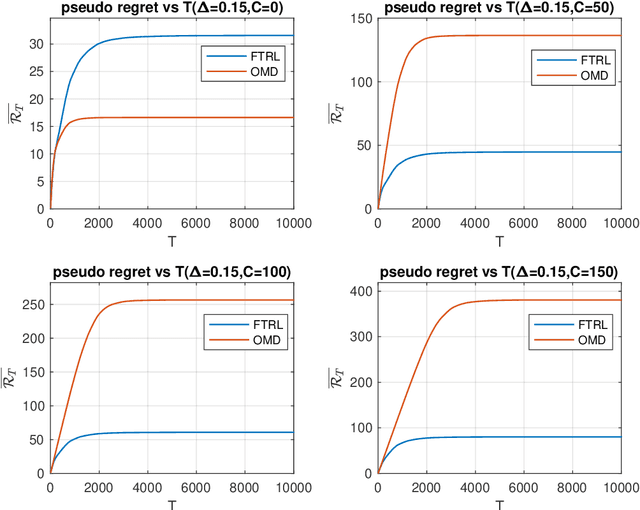
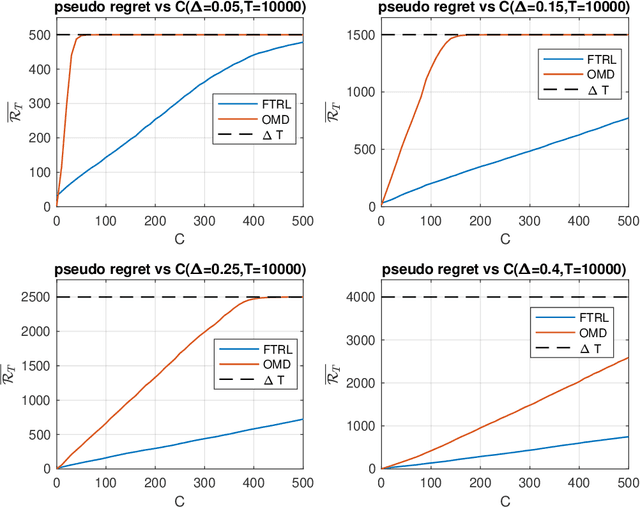
We revisit the fundamental problem of prediction with expert advice, in a setting where the environment is benign and generates losses stochastically, but the feedback observed by the learner is subject to a moderate adversarial corruption. We prove that a variant of the classical Multiplicative Weights algorithm with decreasing step sizes achieves constant regret in this setting and performs optimally in a wide range of environments, regardless of the magnitude of the injected corruption. Our results reveal a surprising disparity between the often comparable Follow the Regularized Leader (FTRL) and Online Mirror Descent (OMD) frameworks: we show that for experts in the corrupted stochastic regime, the regret performance of OMD is in fact strictly inferior to that of FTRL.

Second Order Optimization Made Practical

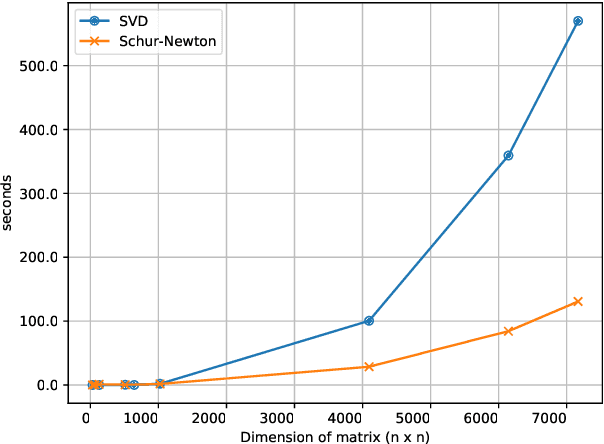
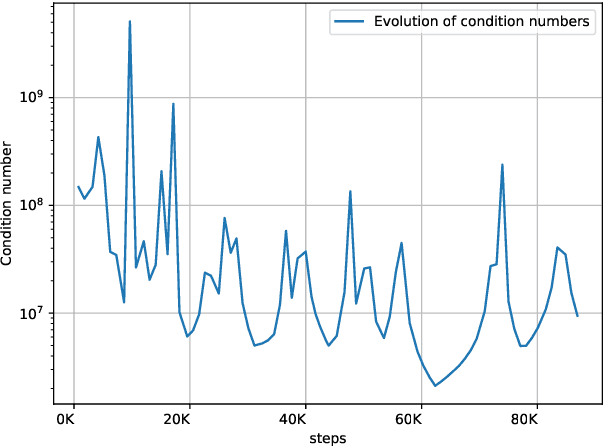
Optimization in machine learning, both theoretical and applied, is presently dominated by first-order gradient methods such as stochastic gradient descent. Second-order optimization methods that involve second-order derivatives and/or second-order statistics of the data have become far less prevalent despite strong theoretical properties, due to their prohibitive computation, memory and communication costs. In an attempt to bridge this gap between theoretical and practical optimization, we present a proof-of-concept distributed system implementation of a second-order preconditioned method (specifically, a variant of full-matrix Adagrad), that along with a few yet critical algorithmic and numerical improvements, provides significant practical gains in convergence on state-of-the-art deep models and gives rise to actual wall-time improvements in practice compared to conventional first-order methods. Our design effectively utilizes the prevalent heterogeneous hardware architecture for training deep models which consists of a multicore CPU coupled with multiple accelerator units. We demonstrate superior performance on very large learning problems in machine translation where our distributed implementation runs considerably faster than existing gradient-based methods.

Logarithmic Regret for Learning Linear Quadratic Regulators Efficiently

We consider the problem of learning in Linear Quadratic Control systems whose transition parameters are initially unknown. Recent results in this setting have demonstrated efficient learning algorithms with regret growing with the square root of the number of decision steps. We present new efficient algorithms that achieve, perhaps surprisingly, regret that scales only (poly)logarithmically with the number of steps in two scenarios: when only the state transition matrix $A$ is unknown, and when only the state-action transition matrix $B$ is unknown and the optimal policy satisfies a certain non-degeneracy condition. On the other hand, we give a lower bound that shows that when the latter condition is violated, square root regret is unavoidable.