Dueling Convex Optimization with General Preferences

We address the problem of \emph{convex optimization with dueling feedback}, where the goal is to minimize a convex function given a weaker form of \emph{dueling} feedback. Each query consists of two points and the dueling feedback returns a (noisy) single-bit binary comparison of the function values of the two queried points. The translation of the function values to the single comparison bit is through a \emph{transfer function}. This problem has been addressed previously for some restricted classes of transfer functions, but here we consider a very general transfer function class which includes all functions that can be approximated by a finite polynomial with a minimal degree $p$. Our main contribution is an efficient algorithm with convergence rate of $\smash{\widetilde O}(\epsilon^{-4p})$ for a smooth convex objective function, and an optimal rate of $\smash{\widetilde O}(\epsilon^{-2p})$ when the objective is smooth and strongly convex.

Regret Minimization and Convergence to Equilibria in General-sum Markov Games

An abundance of recent impossibility results establish that regret minimization in Markov games with adversarial opponents is both statistically and computationally intractable. Nevertheless, none of these results preclude the possibility of regret minimization under the assumption that all parties adopt the same learning procedure. In this work, we present the first (to our knowledge) algorithm for learning in general-sum Markov games that provides sublinear regret guarantees when executed by all agents. The bounds we obtain are for swap regret, and thus, along the way, imply convergence to a correlated equilibrium. Our algorithm is decentralized, computationally efficient, and does not require any communication between agents. Our key observation is that online learning via policy optimization in Markov games essentially reduces to a form of weighted regret minimization, with unknown weights determined by the path length of the agents' policy sequence. Consequently, controlling the path length leads to weighted regret objectives for which sufficiently adaptive algorithms provide sublinear regret guarantees.

Uniform Stability for First-Order Empirical Risk Minimization

We consider the problem of designing uniformly stable first-order optimization algorithms for empirical risk minimization. Uniform stability is often used to obtain generalization error bounds for optimization algorithms, and we are interested in a general approach to achieve it. For Euclidean geometry, we suggest a black-box conversion which given a smooth optimization algorithm, produces a uniformly stable version of the algorithm while maintaining its convergence rate up to logarithmic factors. Using this reduction we obtain a (nearly) optimal algorithm for smooth optimization with convergence rate $\widetilde{O}(1/T^2)$ and uniform stability $O(T^2/n)$, resolving an open problem of Chen et al. (2018); Attia and Koren (2021). For more general geometries, we develop a variant of Mirror Descent for smooth optimization with convergence rate $\widetilde{O}(1/T)$ and uniform stability $O(T/n)$, leaving open the question of devising a general conversion method as in the Euclidean case.

Better Best of Both Worlds Bounds for Bandits with Switching Costs

We study best-of-both-worlds algorithms for bandits with switching cost, recently addressed by Rouyer, Seldin and Cesa-Bianchi, 2021. We introduce a surprisingly simple and effective algorithm that simultaneously achieves minimax optimal regret bound of $\mathcal{O}(T^{2/3})$ in the oblivious adversarial setting and a bound of $\mathcal{O}(\min\{\log (T)/\Delta^2,T^{2/3}\})$ in the stochastically-constrained regime, both with (unit) switching costs, where $\Delta$ is the gap between the arms. In the stochastically constrained case, our bound improves over previous results due to Rouyer et al., that achieved regret of $\mathcal{O}(T^{1/3}/\Delta)$. We accompany our results with a lower bound showing that, in general, $\tilde{\Omega}(\min\{1/\Delta^2,T^{2/3}\})$ regret is unavoidable in the stochastically-constrained case for algorithms with $\mathcal{O}(T^{2/3})$ worst-case regret.

Rate-Optimal Online Convex Optimization in Adaptive Linear Control

We consider the problem of controlling an unknown linear dynamical system under adversarially changing convex costs and full feedback of both the state and cost function. We present the first computationally-efficient algorithm that attains an optimal $\smash{\sqrt{T}}$-regret rate compared to the best stabilizing linear controller in hindsight, while avoiding stringent assumptions on the costs such as strong convexity. Our approach is based on a careful design of non-convex lower confidence bounds for the online costs, and uses a novel technique for computationally-efficient regret minimization of these bounds that leverages their particular non-convex structure.

Efficient Online Linear Control with Stochastic Convex Costs and Unknown Dynamics

We consider the problem of controlling an unknown linear dynamical system under a stochastic convex cost and full feedback of both the state and cost function. We present a computationally efficient algorithm that attains an optimal $\sqrt{T}$ regret-rate against the best stabilizing linear controller. In contrast to previous work, our algorithm is based on the Optimism in the Face of Uncertainty paradigm. This results in a substantially improved computational complexity and a simpler analysis.

Benign Underfitting of Stochastic Gradient Descent

We study to what extent may stochastic gradient descent (SGD) be understood as a "conventional" learning rule that achieves generalization performance by obtaining a good fit to training data. We consider the fundamental stochastic convex optimization framework, where (one pass, without-replacement) SGD is classically known to minimize the population risk at rate $O(1/\sqrt n)$, and prove that, surprisingly, there exist problem instances where the SGD solution exhibits both empirical risk and generalization gap of $\Omega(1)$. Consequently, it turns out that SGD is not algorithmically stable in any sense, and its generalization ability cannot be explained by uniform convergence or any other currently known generalization bound technique for that matter (other than that of its classical analysis). We then continue to analyze the closely related with-replacement SGD, for which we show that an analogous phenomenon does not occur and prove that its population risk does in fact converge at the optimal rate. Finally, we interpret our main results in the context of without-replacement SGD for finite-sum convex optimization problems, and derive upper and lower bounds for the multi-epoch regime that significantly improve upon previously known results.

Stability vs Implicit Bias of Gradient Methods on Separable Data and Beyond

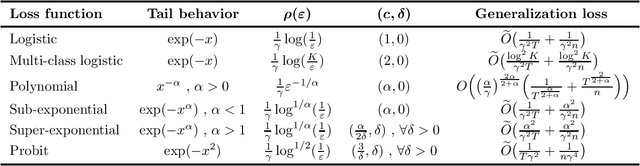
An influential line of recent work has focused on the generalization properties of unregularized gradient-based learning procedures applied to separable linear classification with exponentially-tailed loss functions. The ability of such methods to generalize well has been attributed to the their implicit bias towards large margin predictors, both asymptotically as well as in finite time. We give an additional unified explanation for this generalization and relate it to two simple properties of the optimization objective, that we refer to as realizability and self-boundedness. We introduce a general setting of unconstrained stochastic convex optimization with these properties, and analyze generalization of gradient methods through the lens of algorithmic stability. In this broader setting, we obtain sharp stability bounds for gradient descent and stochastic gradient descent which apply even for a very large number of gradient steps, and use them to derive general generalization bounds for these algorithms. Finally, as direct applications of the general bounds, we return to the setting of linear classification with separable data and establish several novel test loss and test accuracy bounds for gradient descent and stochastic gradient descent for a variety of loss functions with different tail decay rates. In some of these case, our bounds significantly improve upon the existing generalization error bounds in the literature.

Best-of-All-Worlds Bounds for Online Learning with Feedback Graphs

We study the online learning with feedback graphs framework introduced by Mannor and Shamir (2011), in which the feedback received by the online learner is specified by a graph $G$ over the available actions. We develop an algorithm that simultaneously achieves regret bounds of the form: $\smash{\mathcal{O}(\sqrt{\theta(G) T})}$ with adversarial losses; $\mathcal{O}(\theta(G)\operatorname{polylog}{T})$ with stochastic losses; and $\mathcal{O}(\theta(G)\operatorname{polylog}{T} + \smash{\sqrt{\theta(G) C})}$ with stochastic losses subject to $C$ adversarial corruptions. Here, $\theta(G)$ is the clique covering number of the graph $G$. Our algorithm is an instantiation of Follow-the-Regularized-Leader with a novel regularization that can be seen as a product of a Tsallis entropy component (inspired by Zimmert and Seldin (2019)) and a Shannon entropy component (analyzed in the corrupted stochastic case by Amir et al. (2020)), thus subtly interpolating between the two forms of entropies. One of our key technical contributions is in establishing the convexity of this regularizer and controlling its inverse Hessian, despite its complex product structure.

Never Go Full Batch (in Stochastic Convex Optimization)

We study the generalization performance of $\text{full-batch}$ optimization algorithms for stochastic convex optimization: these are first-order methods that only access the exact gradient of the empirical risk (rather than gradients with respect to individual data points), that include a wide range of algorithms such as gradient descent, mirror descent, and their regularized and/or accelerated variants. We provide a new separation result showing that, while algorithms such as stochastic gradient descent can generalize and optimize the population risk to within $\epsilon$ after $O(1/\epsilon^2)$ iterations, full-batch methods either need at least $\Omega(1/\epsilon^4)$ iterations or exhibit a dimension-dependent sample complexity.