In-Context Operator Learning for Linear Propagator Models

We study operator learning in the context of linear propagator models for optimal order execution problems with transient price impact \`a la Bouchaud et al. (2004) and Gatheral (2010). Transient price impact persists and decays over time according to some propagator kernel. Specifically, we propose to use In-Context Operator Networks (ICON), a novel transformer-based neural network architecture introduced by Yang et al. (2023), which facilitates data-driven learning of operators by merging offline pre-training with an online few-shot prompting inference. First, we train ICON to learn the operator from various propagator models that maps the trading rate to the induced transient price impact. The inference step is then based on in-context prediction, where ICON is presented only with a few examples. We illustrate that ICON is capable of accurately inferring the underlying price impact model from the data prompts, even with propagator kernels not seen in the training data. In a second step, we employ the pre-trained ICON model provided with context as a surrogate operator in solving an optimal order execution problem via a neural network control policy, and demonstrate that the exact optimal execution strategies from Abi Jaber and Neuman (2022) for the models generating the context are correctly retrieved. Our introduced methodology is very general, offering a new approach to solving optimal stochastic control problems with unknown state dynamics, inferred data-efficiently from a limited number of examples by leveraging the few-shot and transfer learning capabilities of transformer networks.

HJ-sampler: A Bayesian sampler for inverse problems of a stochastic process by leveraging Hamilton-Jacobi PDEs and score-based generative models

The interplay between stochastic processes and optimal control has been extensively explored in the literature. With the recent surge in the use of diffusion models, stochastic processes have increasingly been applied to sample generation. This paper builds on the log transform, known as the Cole-Hopf transform in Brownian motion contexts, and extends it within a more abstract framework that includes a linear operator. Within this framework, we found that the well-known relationship between the Cole-Hopf transform and optimal transport is a particular instance where the linear operator acts as the infinitesimal generator of a stochastic process. We also introduce a novel scenario where the linear operator is the adjoint of the generator, linking to Bayesian inference under specific initial and terminal conditions. Leveraging this theoretical foundation, we develop a new algorithm, named the HJ-sampler, for Bayesian inference for the inverse problem of a stochastic differential equation with given terminal observations. The HJ-sampler involves two stages: (1) solving the viscous Hamilton-Jacobi partial differential equations, and (2) sampling from the associated stochastic optimal control problem. Our proposed algorithm naturally allows for flexibility in selecting the numerical solver for viscous HJ PDEs. We introduce two variants of the solver: the Riccati-HJ-sampler, based on the Riccati method, and the SGM-HJ-sampler, which utilizes diffusion models. We demonstrate the effectiveness and flexibility of the proposed methods by applying them to solve Bayesian inverse problems involving various stochastic processes and prior distributions, including applications that address model misspecifications and quantifying model uncertainty.

Leveraging viscous Hamilton-Jacobi PDEs for uncertainty quantification in scientific machine learning

Uncertainty quantification (UQ) in scientific machine learning (SciML) combines the powerful predictive power of SciML with methods for quantifying the reliability of the learned models. However, two major challenges remain: limited interpretability and expensive training procedures. We provide a new interpretation for UQ problems by establishing a new theoretical connection between some Bayesian inference problems arising in SciML and viscous Hamilton-Jacobi partial differential equations (HJ PDEs). Namely, we show that the posterior mean and covariance can be recovered from the spatial gradient and Hessian of the solution to a viscous HJ PDE. As a first exploration of this connection, we specialize to Bayesian inference problems with linear models, Gaussian likelihoods, and Gaussian priors. In this case, the associated viscous HJ PDEs can be solved using Riccati ODEs, and we develop a new Riccati-based methodology that provides computational advantages when continuously updating the model predictions. Specifically, our Riccati-based approach can efficiently add or remove data points to the training set invariant to the order of the data and continuously tune hyperparameters. Moreover, neither update requires retraining on or access to previously incorporated data. We provide several examples from SciML involving noisy data and \textit{epistemic uncertainty} to illustrate the potential advantages of our approach. In particular, this approach's amenability to data streaming applications demonstrates its potential for real-time inferences, which, in turn, allows for applications in which the predicted uncertainty is used to dynamically alter the learning process.

Leveraging Hamilton-Jacobi PDEs with time-dependent Hamiltonians for continual scientific machine learning

We address two major challenges in scientific machine learning (SciML): interpretability and computational efficiency. We increase the interpretability of certain learning processes by establishing a new theoretical connection between optimization problems arising from SciML and a generalized Hopf formula, which represents the viscosity solution to a Hamilton-Jacobi partial differential equation (HJ PDE) with time-dependent Hamiltonian. Namely, we show that when we solve certain regularized learning problems with integral-type losses, we actually solve an optimal control problem and its associated HJ PDE with time-dependent Hamiltonian. This connection allows us to reinterpret incremental updates to learned models as the evolution of an associated HJ PDE and optimal control problem in time, where all of the previous information is intrinsically encoded in the solution to the HJ PDE. As a result, existing HJ PDE solvers and optimal control algorithms can be reused to design new efficient training approaches for SciML that naturally coincide with the continual learning framework, while avoiding catastrophic forgetting. As a first exploration of this connection, we consider the special case of linear regression and leverage our connection to develop a new Riccati-based methodology for solving these learning problems that is amenable to continual learning applications. We also provide some corresponding numerical examples that demonstrate the potential computational and memory advantages our Riccati-based approach can provide.

Prompting In-Context Operator Learning with Sensor Data, Equations, and Natural Language

In the growing domain of scientific machine learning, in-context operator learning has demonstrated notable potential in learning operators from prompted data during inference stage without weight updates. However, the current model's overdependence on sensor data, may inadvertently overlook the invaluable human insight into the operator. To address this, we present a transformation of in-context operator learning into a multi-modal paradigm. We propose the use of "captions" to integrate human knowledge about the operator, expressed through natural language descriptions and equations. We illustrate how this method not only broadens the flexibility and generality of physics-informed learning, but also significantly boosts learning performance and reduces data needs. Furthermore, we introduce a more efficient neural network architecture for multi-modal in-context operator learning, referred to as "ICON-LM", based on a language-model-like architecture. We demonstrate the viability of "ICON-LM" for scientific machine learning tasks, which creates a new path for the application of language models.

In-Context Operator Learning for Differential Equation Problems

This paper introduces a new neural-network-based approach, namely IN-context Differential Equation Encoder-Decoder (INDEED), to simultaneously learn operators from data and apply it to new questions during the inference stage, without any weight update. Existing methods are limited to using a neural network to approximate a specific equation solution or a specific operator, requiring retraining when switching to a new problem with different equations. By training a single neural network as an operator learner, we can not only get rid of retraining (even fine-tuning) the neural network for new problems, but also leverage the commonalities shared across operators so that only a few demos are needed when learning a new operator. Our numerical results show the neural network's capability as a few-shot operator learner for a diversified type of differential equation problems, including forward and inverse problems of ODEs and PDEs, and also show that it can generalize its learning capability to operators beyond the training distribution, even to an unseen type of operator.

Leveraging Multi-time Hamilton-Jacobi PDEs for Certain Scientific Machine Learning Problems

Hamilton-Jacobi partial differential equations (HJ PDEs) have deep connections with a wide range of fields, including optimal control, differential games, and imaging sciences. By considering the time variable to be a higher dimensional quantity, HJ PDEs can be extended to the multi-time case. In this paper, we establish a novel theoretical connection between specific optimization problems arising in machine learning and the multi-time Hopf formula, which corresponds to a representation of the solution to certain multi-time HJ PDEs. Through this connection, we increase the interpretability of the training process of certain machine learning applications by showing that when we solve these learning problems, we also solve a multi-time HJ PDE and, by extension, its corresponding optimal control problem. As a first exploration of this connection, we develop the relation between the regularized linear regression problem and the Linear Quadratic Regulator (LQR). We then leverage our theoretical connection to adapt standard LQR solvers (namely, those based on the Riccati ordinary differential equations) to design new training approaches for machine learning. Finally, we provide some numerical examples that demonstrate the versatility and possible computational advantages of our Riccati-based approach in the context of continual learning, post-training calibration, transfer learning, and sparse dynamics identification.

SympOCnet: Solving optimal control problems with applications to high-dimensional multi-agent path planning problems

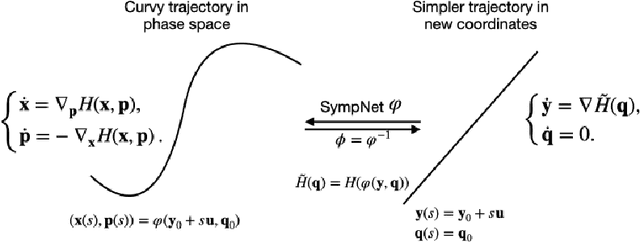
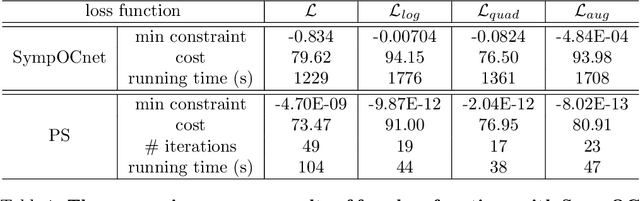
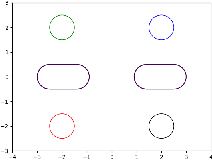
Solving high-dimensional optimal control problems in real-time is an important but challenging problem, with applications to multi-agent path planning problems, which have drawn increased attention given the growing popularity of drones in recent years. In this paper, we propose a novel neural network method called SympOCnet that applies the Symplectic network to solve high-dimensional optimal control problems with state constraints. We present several numerical results on path planning problems in two-dimensional and three-dimensional spaces. Specifically, we demonstrate that our SympOCnet can solve a problem with more than 500 dimensions in 1.5 hours on a single GPU, which shows the effectiveness and efficiency of SympOCnet. The proposed method is scalable and has the potential to solve truly high-dimensional path planning problems in real-time.

On Hamilton-Jacobi PDEs and image denoising models with certain non-additive noise

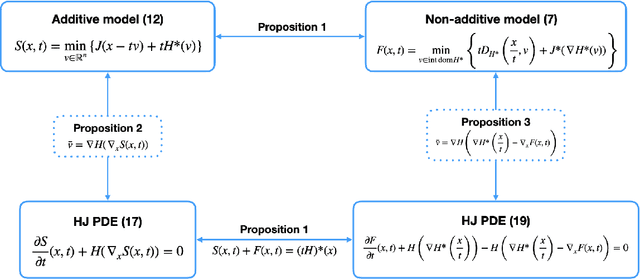
We consider image denoising problems formulated as variational problems. It is known that Hamilton-Jacobi PDEs govern the solution of such optimization problems when the noise model is additive. In this work, we address certain non-additive noise models and show that they are also related to Hamilton-Jacobi PDEs. These findings allow us to establish new connections between additive and non-additive noise imaging models. With these connections, some non-convex models for non-additive noise can be solved by applying convex optimization algorithms to the equivalent convex models for additive noise. Several numerical results are provided for denoising problems with Poisson noise or multiplicative noise.

Neural network architectures using min plus algebra for solving certain high dimensional optimal control problems and Hamilton-Jacobi PDEs

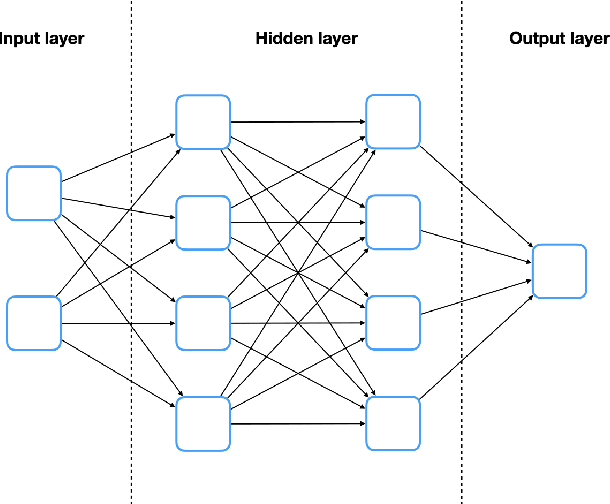
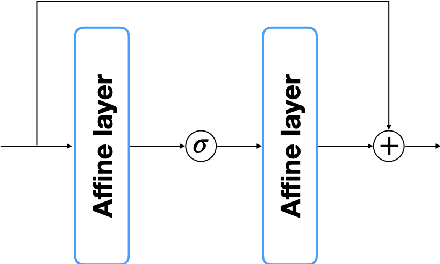
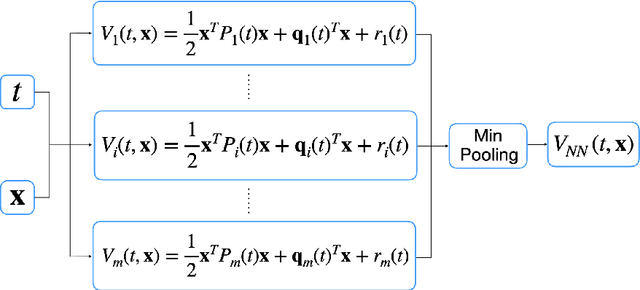
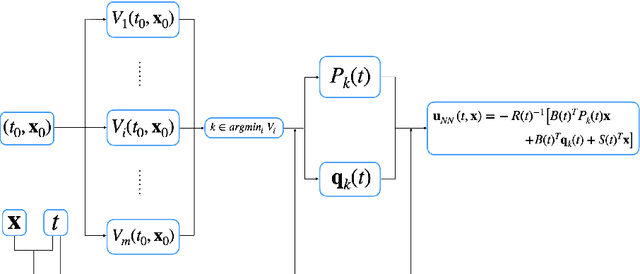
Solving high dimensional optimal control problems and corresponding Hamilton-Jacobi PDEs are important but challenging problems in control engineering. In this paper, we propose two abstract neural network architectures which respectively represent the value function and the state feedback characterisation of the optimal control for certain class of high dimensional optimal control problems. We provide the mathematical analysis for the two abstract architectures. We also show several numerical results computed using the deep neural network implementations of these abstract architectures. This work paves the way to leverage efficient dedicated hardware designed for neural networks to solve high dimensional optimal control problems and Hamilton-Jacobi PDEs.