The Power of Regularization in Solving Extensive-Form Games

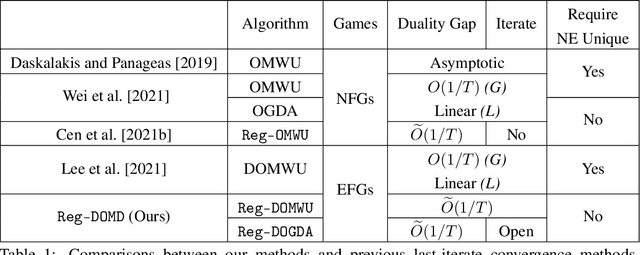
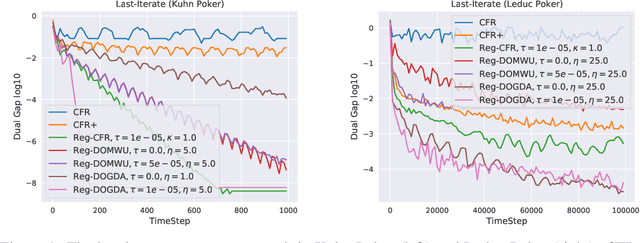
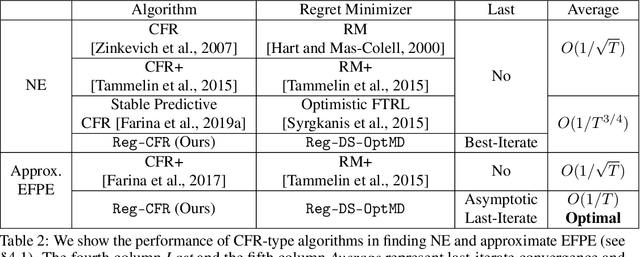
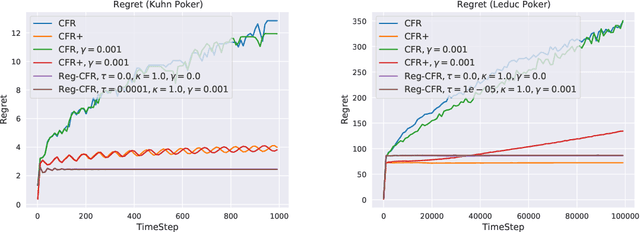
In this paper, we investigate the power of regularization, a common technique in reinforcement learning and optimization, in solving extensive-form games (EFGs). We propose a series of new algorithms based on regularizing the payoff functions of the game, and establish a set of convergence results that strictly improve over the existing ones, with either weaker assumptions or stronger convergence guarantees. In particular, we first show that dilated optimistic mirror descent (DOMD), an efficient variant of OMD for solving EFGs, with adaptive regularization can achieve a fast $\tilde O(1/T)$ last-iterate convergence in terms of duality gap without the uniqueness assumption of the Nash equilibrium (NE). Moreover, regularized dilated optimistic multiplicative weights update (Reg-DOMWU), an instance of Reg-DOMD, further enjoys the $\tilde O(1/T)$ last-iterate convergence rate of the distance to the set of NE. This addresses an open question on whether iterate convergence can be obtained for OMWU algorithms without the uniqueness assumption in both the EFG and normal-form game literature. Second, we show that regularized counterfactual regret minimization (Reg-CFR), with a variant of optimistic mirror descent algorithm as regret-minimizer, can achieve $O(1/T^{1/4})$ best-iterate, and $O(1/T^{3/4})$ average-iterate convergence rate for finding NE in EFGs. Finally, we show that Reg-CFR can achieve asymptotic last-iterate convergence, and optimal $O(1/T)$ average-iterate convergence rate, for finding the NE of perturbed EFGs, which is useful for finding approximate extensive-form perfect equilibria (EFPE). To the best of our knowledge, they constitute the first last-iterate convergence results for CFR-type algorithms, while matching the SOTA average-iterate convergence rate in finding NE for non-perturbed EFGs. We also provide numerical results to corroborate the advantages of our algorithms.

Efficient $Φ$-Regret Minimization in Extensive-Form Games via Online Mirror Descent

A conceptually appealing approach for learning Extensive-Form Games (EFGs) is to convert them to Normal-Form Games (NFGs). This approach enables us to directly translate state-of-the-art techniques and analyses in NFGs to learning EFGs, but typically suffers from computational intractability due to the exponential blow-up of the game size introduced by the conversion. In this paper, we address this problem in natural and important setups for the \emph{$\Phi$-Hedge} algorithm -- A generic algorithm capable of learning a large class of equilibria for NFGs. We show that $\Phi$-Hedge can be directly used to learn Nash Equilibria (zero-sum settings), Normal-Form Coarse Correlated Equilibria (NFCCE), and Extensive-Form Correlated Equilibria (EFCE) in EFGs. We prove that, in those settings, the \emph{$\Phi$-Hedge} algorithms are equivalent to standard Online Mirror Descent (OMD) algorithms for EFGs with suitable dilated regularizers, and run in polynomial time. This new connection further allows us to design and analyze a new class of OMD algorithms based on modifying its log-partition function. In particular, we design an improved algorithm with balancing techniques that achieves a sharp $\widetilde{\mathcal{O}}(\sqrt{XAT})$ EFCE-regret under bandit-feedback in an EFG with $X$ information sets, $A$ actions, and $T$ episodes. To our best knowledge, this is the first such rate and matches the information-theoretic lower bound.

Near-Optimal Learning of Extensive-Form Games with Imperfect Information

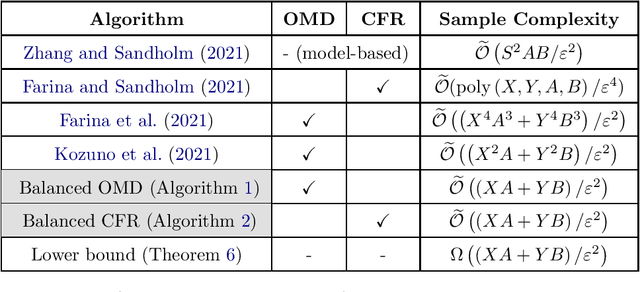
This paper resolves the open question of designing near-optimal algorithms for learning imperfect-information extensive-form games from bandit feedback. We present the first line of algorithms that require only $\widetilde{\mathcal{O}}((XA+YB)/\varepsilon^2)$ episodes of play to find an $\varepsilon$-approximate Nash equilibrium in two-player zero-sum games, where $X,Y$ are the number of information sets and $A,B$ are the number of actions for the two players. This improves upon the best known sample complexity of $\widetilde{\mathcal{O}}((X^2A+Y^2B)/\varepsilon^2)$ by a factor of $\widetilde{\mathcal{O}}(\max\{X, Y\})$, and matches the information-theoretic lower bound up to logarithmic factors. We achieve this sample complexity by two new algorithms: Balanced Online Mirror Descent, and Balanced Counterfactual Regret Minimization. Both algorithms rely on novel approaches of integrating \emph{balanced exploration policies} into their classical counterparts. We also extend our results to learning Coarse Correlated Equilibria in multi-player general-sum games.

V-Learning -- A Simple, Efficient, Decentralized Algorithm for Multiagent RL

A major challenge of multiagent reinforcement learning (MARL) is the curse of multiagents, where the size of the joint action space scales exponentially with the number of agents. This remains to be a bottleneck for designing efficient MARL algorithms even in a basic scenario with finitely many states and actions. This paper resolves this challenge for the model of episodic Markov games. We design a new class of fully decentralized algorithms -- V-learning, which provably learns Nash equilibria (in the two-player zero-sum setting), correlated equilibria and coarse correlated equilibria (in the multiplayer general-sum setting) in a number of samples that only scales with $\max_{i\in[m]} A_i$, where $A_i$ is the number of actions for the $i^{\rm th}$ player. This is in sharp contrast to the size of the joint action space which is $\prod_{i=1}^m A_i$. V-learning (in its basic form) is a new class of single-agent RL algorithms that convert any adversarial bandit algorithm with suitable regret guarantees into a RL algorithm. Similar to the classical Q-learning algorithm, it performs incremental updates to the value functions. Different from Q-learning, it only maintains the estimates of V-values instead of Q-values. This key difference allows V-learning to achieve the claimed guarantees in the MARL setting by simply letting all agents run V-learning independently.

The Power of Exploiter: Provable Multi-Agent RL in Large State Spaces

Modern reinforcement learning (RL) commonly engages practical problems with large state spaces, where function approximation must be deployed to approximate either the value function or the policy. While recent progresses in RL theory address a rich set of RL problems with general function approximation, such successes are mostly restricted to the single-agent setting. It remains elusive how to extend these results to multi-agent RL, especially due to the new challenges arising from its game-theoretical nature. This paper considers two-player zero-sum Markov Games (MGs). We propose a new algorithm that can provably find the Nash equilibrium policy using a polynomial number of samples, for any MG with low multi-agent Bellman-Eluder dimension -- a new complexity measure adapted from its single-agent version (Jin et al., 2021). A key component of our new algorithm is the exploiter, which facilitates the learning of the main player by deliberately exploiting her weakness. Our theoretical framework is generic, which applies to a wide range of models including but not limited to tabular MGs, MGs with linear or kernel function approximation, and MGs with rich observations.

Provably Efficient Algorithms for Multi-Objective Competitive RL

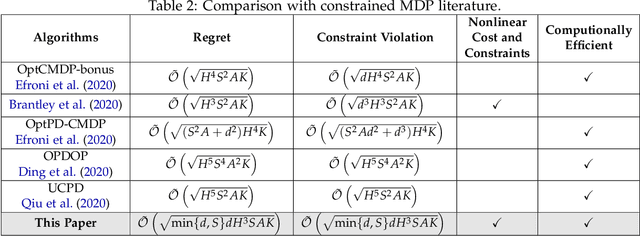
We study multi-objective reinforcement learning (RL) where an agent's reward is represented as a vector. In settings where an agent competes against opponents, its performance is measured by the distance of its average return vector to a target set. We develop statistically and computationally efficient algorithms to approach the associated target set. Our results extend Blackwell's approachability theorem (Blackwell, 1956) to tabular RL, where strategic exploration becomes essential. The algorithms presented are adaptive; their guarantees hold even without Blackwell's approachability condition. If the opponents use fixed policies, we give an improved rate of approaching the target set while also tackling the more ambitious goal of simultaneously minimizing a scalar cost function. We discuss our analysis for this special case by relating our results to previous works on constrained RL. To our knowledge, this work provides the first provably efficient algorithms for vector-valued Markov games and our theoretical guarantees are near-optimal.

Provably Efficient Online Agnostic Learning in Markov Games

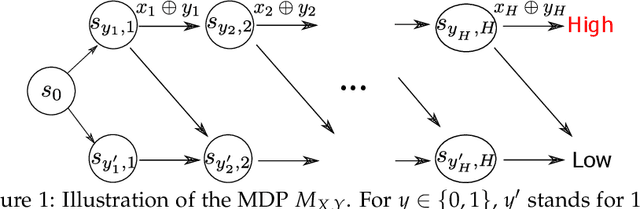
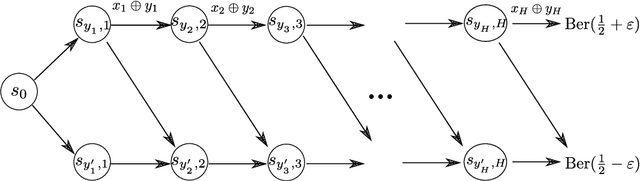
We study online agnostic learning, a problem that arises in episodic multi-agent reinforcement learning where the actions of the opponents are unobservable. We show that in this challenging setting, achieving sublinear regret against the best response in hindsight is statistically hard. We then consider a weaker notion of regret, and present an algorithm that achieves after $K$ episodes a sublinear $\tilde{\mathcal{O}}(K^{3/4})$ regret. This is the first sublinear regret bound (to our knowledge) in the online agnostic setting. Importantly, our regret bound is independent of the size of the opponents' action spaces. As a result, even when the opponents' actions are fully observable, our regret bound improves upon existing analysis (e.g., (Xie et al., 2020)) by an exponential factor in the number of opponents.

A Sharp Analysis of Model-based Reinforcement Learning with Self-Play

Model-based algorithms---algorithms that decouple learning of the model and planning given the model---are widely used in reinforcement learning practice and theoretically shown to achieve optimal sample efficiency for single-agent reinforcement learning in Markov Decision Processes (MDPs). However, for multi-agent reinforcement learning in Markov games, the current best known sample complexity for model-based algorithms is rather suboptimal and compares unfavorably against recent model-free approaches. In this paper, we present a sharp analysis of model-based self-play algorithms for multi-agent Markov games. We design an algorithm \emph{Optimistic Nash Value Iteration} (Nash-VI) for two-player zero-sum Markov games that is able to output an $\epsilon$-approximate Nash policy in $\tilde{\mathcal{O}}(H^3SAB/\epsilon^2)$ episodes of game playing, where $S$ is the number of states, $A,B$ are the number of actions for the two players respectively, and $H$ is the horizon length. This is the first algorithm that matches the information-theoretic lower bound $\Omega(H^3S(A+B)/\epsilon^2)$ except for a $\min\{A,B\}$ factor, and compares favorably against the best known model-free algorithm if $\min\{A,B\}=o(H^3)$. In addition, our Nash-VI outputs a single Markov policy with optimality guarantee, while existing sample-efficient model-free algorithms output a nested mixture of Markov policies that is in general non-Markov and rather inconvenient to store and execute. We further adapt our analysis to designing a provably efficient task-agnostic algorithm for zero-sum Markov games, and designing the first line of provably sample-efficient algorithms for multi-player general-sum Markov games.

Near-Optimal Reinforcement Learning with Self-Play

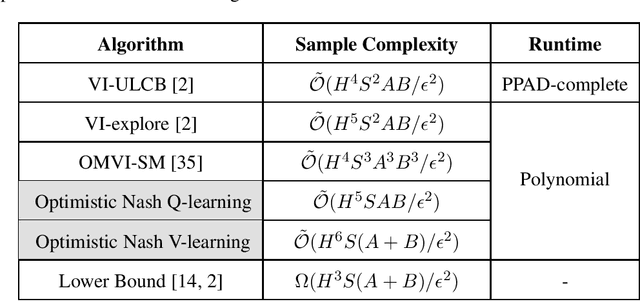
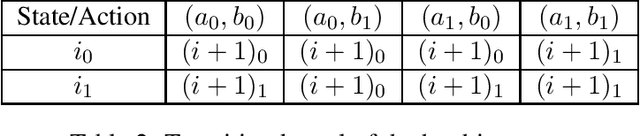
This paper considers the problem of designing optimal algorithms for reinforcement learning in two-player zero-sum games. We focus on self-play algorithms which learn the optimal policy by playing against itself without any direct supervision. In a tabular episodic Markov game with $S$ states, $A$ max-player actions and $B$ min-player actions, the best existing algorithm for finding an approximate Nash equilibrium requires $\tilde{\mathcal{O}}(S^2AB)$ steps of game playing, when only highlighting the dependency on $(S,A,B)$. In contrast, the best existing lower bound scales as $\Omega(S(A+B))$ and has a significant gap from the upper bound. This paper closes this gap for the first time: we propose an optimistic variant of the \emph{Nash Q-learning} algorithm with sample complexity $\tilde{\mathcal{O}}(SAB)$, and a new \emph{Nash V-learning} algorithm with sample complexity $\tilde{\mathcal{O}}(S(A+B))$. The latter result matches the information-theoretic lower bound in all problem-dependent parameters except for a polynomial factor of the length of each episode. In addition, we present a computational hardness result for learning the best responses against a fixed opponent in Markov games---a learning objective different from finding the Nash equilibrium.

A General Framework for Analyzing Stochastic Dynamics in Learning Algorithms

We present a general framework for analyzing high-probability bounds for stochastic dynamics in learning algorithms. Our framework composes standard techniques such as a stopping time, a martingale concentration and a closed-from solution to give a streamlined three-step recipe with a general and flexible principle to implement it. To demonstrate the power and the flexibility of our framework, we apply the framework on three very different learning problems: stochastic gradient descent for strongly convex functions, streaming principal component analysis and linear bandit with stochastic gradient descent updates. We improve the state of the art bounds on all three dynamics.