Topology Reduction in Deep Convolutional Feature Extraction Networks

Deep convolutional neural networks (CNNs) used in practice employ potentially hundreds of layers and $10$,$000$s of nodes. Such network sizes entail significant computational complexity due to the large number of convolutions that need to be carried out; in addition, a large number of parameters needs to be learned and stored. Very deep and wide CNNs may therefore not be well suited to applications operating under severe resource constraints as is the case, e.g., in low-power embedded and mobile platforms. This paper aims at understanding the impact of CNN topology, specifically depth and width, on the network's feature extraction capabilities. We address this question for the class of scattering networks that employ either Weyl-Heisenberg filters or wavelets, the modulus non-linearity, and no pooling. The exponential feature map energy decay results in Wiatowski et al., 2017, are generalized to $\mathcal{O}(a^{-N})$, where an arbitrary decay factor $a>1$ can be realized through suitable choice of the Weyl-Heisenberg prototype function or the mother wavelet. We then show how networks of fixed (possibly small) depth $N$ can be designed to guarantee that $((1-\varepsilon)\cdot 100)\%$ of the input signal's energy are contained in the feature vector. Based on the notion of operationally significant nodes, we characterize, partly rigorously and partly heuristically, the topology-reducing effects of (effectively) band-limited input signals, band-limited filters, and feature map symmetries. Finally, for networks based on Weyl-Heisenberg filters, we determine the prototype function bandwidth that minimizes---for fixed network depth $N$---the average number of operationally significant nodes per layer.

Deep Convolutional Neural Networks on Cartoon Functions

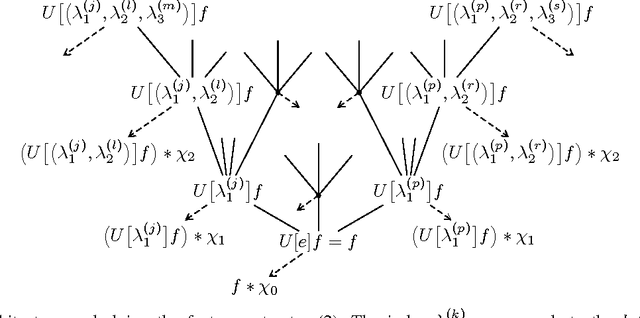
Wiatowski and B\"olcskei, 2015, proved that deformation stability and vertical translation invariance of deep convolutional neural network-based feature extractors are guaranteed by the network structure per se rather than the specific convolution kernels and non-linearities. While the translation invariance result applies to square-integrable functions, the deformation stability bound holds for band-limited functions only. Many signals of practical relevance (such as natural images) exhibit, however, sharp and curved discontinuities and are, hence, not band-limited. The main contribution of this paper is a deformation stability result that takes these structural properties into account. Specifically, we establish deformation stability bounds for the class of cartoon functions introduced by Donoho, 2001.

Energy Propagation in Deep Convolutional Neural Networks

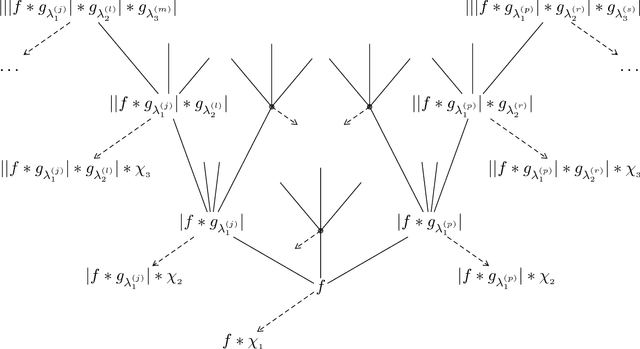
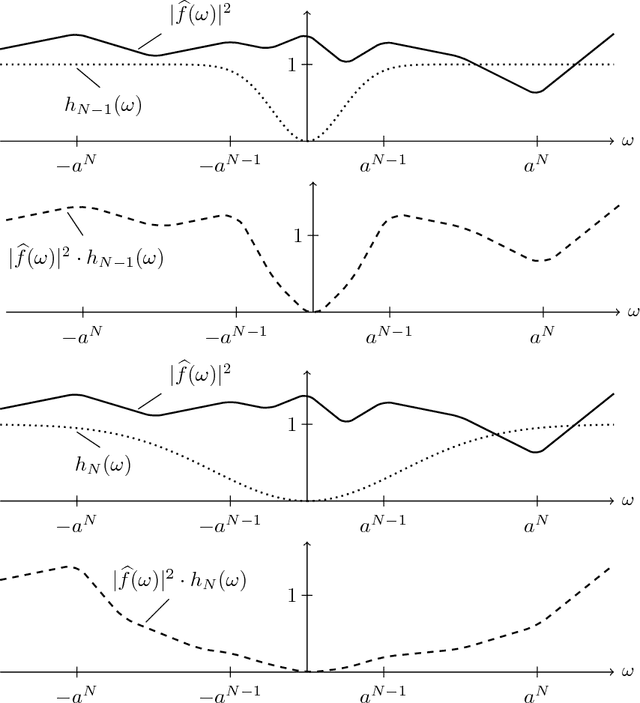
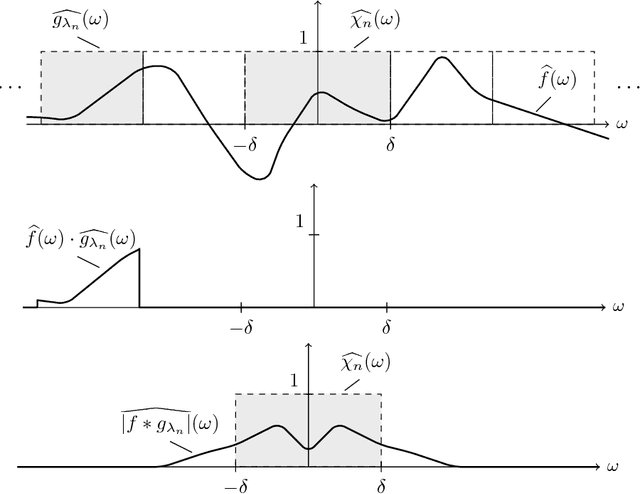
Many practical machine learning tasks employ very deep convolutional neural networks. Such large depths pose formidable computational challenges in training and operating the network. It is therefore important to understand how fast the energy contained in the propagated signals (a.k.a. feature maps) decays across layers. In addition, it is desirable that the feature extractor generated by the network be informative in the sense of the only signal mapping to the all-zeros feature vector being the zero input signal. This "trivial null-set" property can be accomplished by asking for "energy conservation" in the sense of the energy in the feature vector being proportional to that of the corresponding input signal. This paper establishes conditions for energy conservation (and thus for a trivial null-set) for a wide class of deep convolutional neural network-based feature extractors and characterizes corresponding feature map energy decay rates. Specifically, we consider general scattering networks employing the modulus non-linearity and we find that under mild analyticity and high-pass conditions on the filters (which encompass, inter alia, various constructions of Weyl-Heisenberg filters, wavelets, ridgelets, ($\alpha$)-curvelets, and shearlets) the feature map energy decays at least polynomially fast. For broad families of wavelets and Weyl-Heisenberg filters, the guaranteed decay rate is shown to be exponential. Moreover, we provide handy estimates of the number of layers needed to have at least $((1-\varepsilon)\cdot 100)\%$ of the input signal energy be contained in the feature vector.

A Mathematical Theory of Deep Convolutional Neural Networks for Feature Extraction

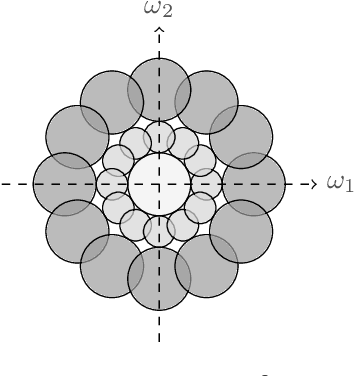
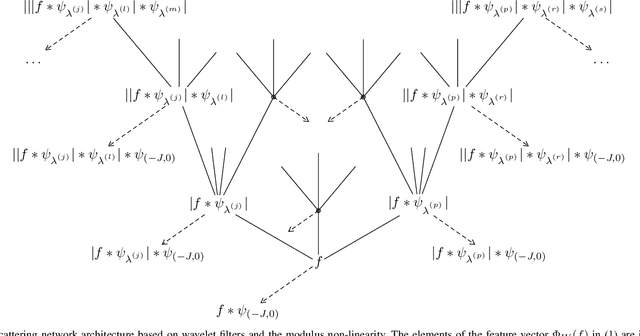
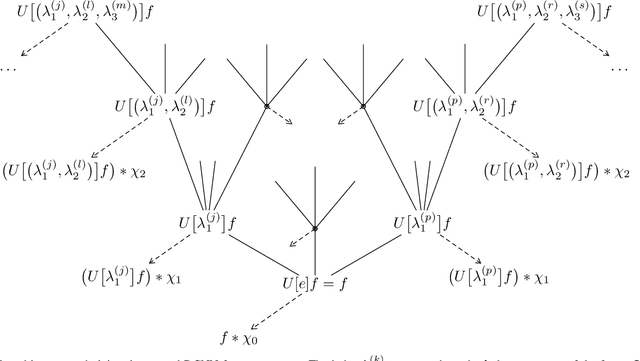
Deep convolutional neural networks have led to breakthrough results in numerous practical machine learning tasks such as classification of images in the ImageNet data set, control-policy-learning to play Atari games or the board game Go, and image captioning. Many of these applications first perform feature extraction and then feed the results thereof into a trainable classifier. The mathematical analysis of deep convolutional neural networks for feature extraction was initiated by Mallat, 2012. Specifically, Mallat considered so-called scattering networks based on a wavelet transform followed by the modulus non-linearity in each network layer, and proved translation invariance (asymptotically in the wavelet scale parameter) and deformation stability of the corresponding feature extractor. This paper complements Mallat's results by developing a theory that encompasses general convolutional transforms, or in more technical parlance, general semi-discrete frames (including Weyl-Heisenberg filters, curvelets, shearlets, ridgelets, wavelets, and learned filters), general Lipschitz-continuous non-linearities (e.g., rectified linear units, shifted logistic sigmoids, hyperbolic tangents, and modulus functions), and general Lipschitz-continuous pooling operators emulating, e.g., sub-sampling and averaging. In addition, all of these elements can be different in different network layers. For the resulting feature extractor we prove a translation invariance result of vertical nature in the sense of the features becoming progressively more translation-invariant with increasing network depth, and we establish deformation sensitivity bounds that apply to signal classes such as, e.g., band-limited functions, cartoon functions, and Lipschitz functions.

Deep Structured Features for Semantic Segmentation

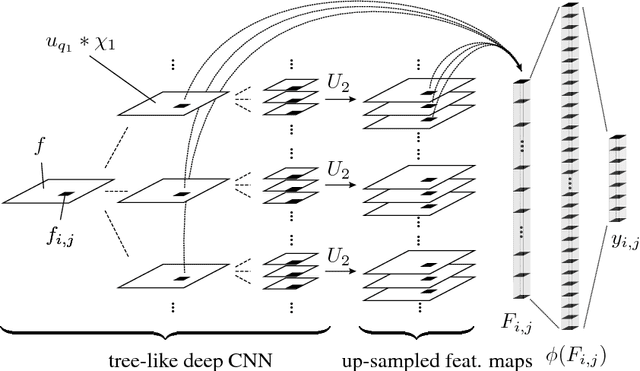
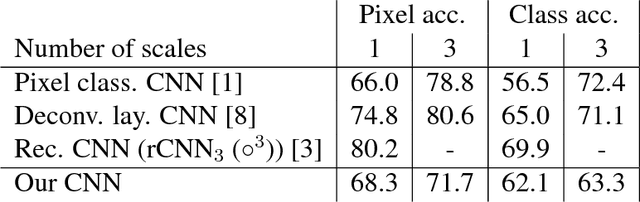
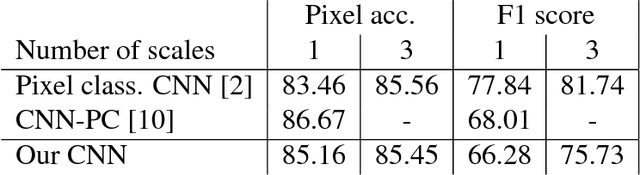
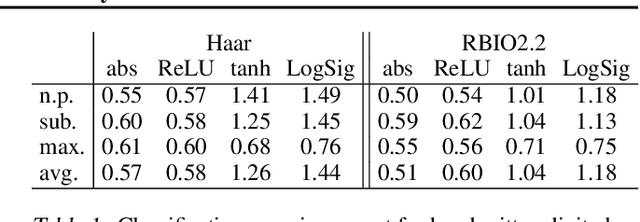
We propose a highly structured neural network architecture for semantic segmentation with an extremely small model size, suitable for low-power embedded and mobile platforms. Specifically, our architecture combines i) a Haar wavelet-based tree-like convolutional neural network (CNN), ii) a random layer realizing a radial basis function kernel approximation, and iii) a linear classifier. While stages i) and ii) are completely pre-specified, only the linear classifier is learned from data. We apply the proposed architecture to outdoor scene and aerial image semantic segmentation and show that the accuracy of our architecture is competitive with conventional pixel classification CNNs. Furthermore, we demonstrate that the proposed architecture is data efficient in the sense of matching the accuracy of pixel classification CNNs when trained on a much smaller data set.

Discrete Deep Feature Extraction: A Theory and New Architectures

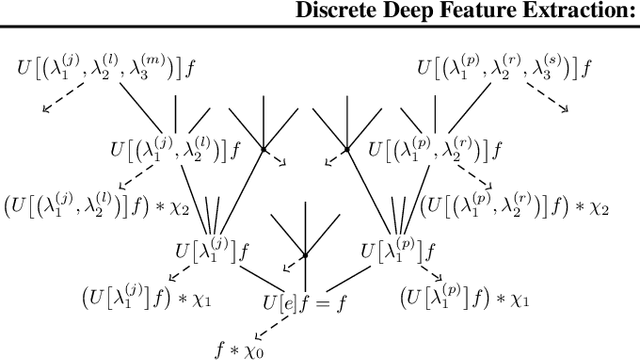
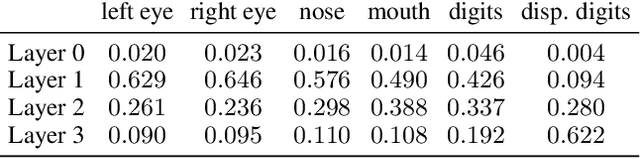
First steps towards a mathematical theory of deep convolutional neural networks for feature extraction were made---for the continuous-time case---in Mallat, 2012, and Wiatowski and B\"olcskei, 2015. This paper considers the discrete case, introduces new convolutional neural network architectures, and proposes a mathematical framework for their analysis. Specifically, we establish deformation and translation sensitivity results of local and global nature, and we investigate how certain structural properties of the input signal are reflected in the corresponding feature vectors. Our theory applies to general filters and general Lipschitz-continuous non-linearities and pooling operators. Experiments on handwritten digit classification and facial landmark detection---including feature importance evaluation---complement the theoretical findings.

Deep Convolutional Neural Networks Based on Semi-Discrete Frames

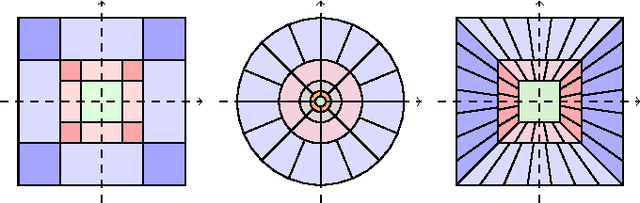
Deep convolutional neural networks have led to breakthrough results in practical feature extraction applications. The mathematical analysis of these networks was pioneered by Mallat, 2012. Specifically, Mallat considered so-called scattering networks based on identical semi-discrete wavelet frames in each network layer, and proved translation-invariance as well as deformation stability of the resulting feature extractor. The purpose of this paper is to develop Mallat's theory further by allowing for different and, most importantly, general semi-discrete frames (such as, e.g., Gabor frames, wavelets, curvelets, shearlets, ridgelets) in distinct network layers. This allows to extract wider classes of features than point singularities resolved by the wavelet transform. Our generalized feature extractor is proven to be translation-invariant, and we develop deformation stability results for a larger class of deformations than those considered by Mallat. For Mallat's wavelet-based feature extractor, we get rid of a number of technical conditions. The mathematical engine behind our results is continuous frame theory, which allows us to completely detach the invariance and deformation stability proofs from the particular algebraic structure of the underlying frames.