Discrete Deep Feature Extraction: A Theory and New Architectures

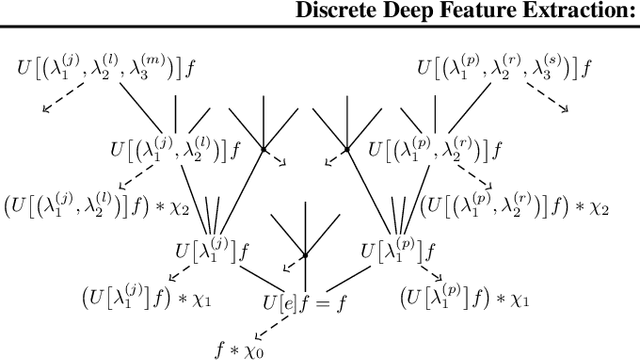
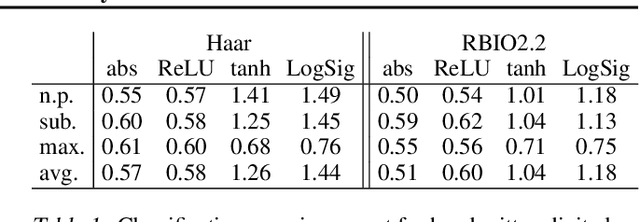
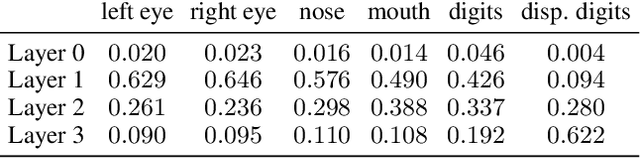
First steps towards a mathematical theory of deep convolutional neural networks for feature extraction were made---for the continuous-time case---in Mallat, 2012, and Wiatowski and B\"olcskei, 2015. This paper considers the discrete case, introduces new convolutional neural network architectures, and proposes a mathematical framework for their analysis. Specifically, we establish deformation and translation sensitivity results of local and global nature, and we investigate how certain structural properties of the input signal are reflected in the corresponding feature vectors. Our theory applies to general filters and general Lipschitz-continuous non-linearities and pooling operators. Experiments on handwritten digit classification and facial landmark detection---including feature importance evaluation---complement the theoretical findings.