Semi-supervised Nonnegative Matrix Factorization for Document Classification

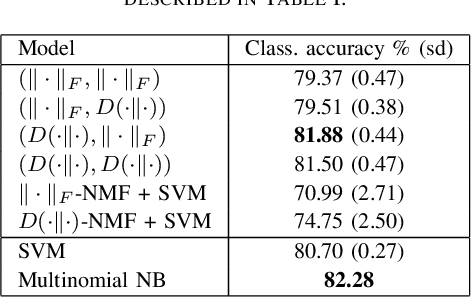
We propose new semi-supervised nonnegative matrix factorization (SSNMF) models for document classification and provide motivation for these models as maximum likelihood estimators. The proposed SSNMF models simultaneously provide both a topic model and a model for classification, thereby offering highly interpretable classification results. We derive training methods using multiplicative updates for each new model, and demonstrate the application of these models to single-label and multi-label document classification, although the models are flexible to other supervised learning tasks such as regression. We illustrate the promise of these models and training methods on document classification datasets (e.g., 20 Newsgroups, Reuters).

Geometry of Linear Convolutional Networks

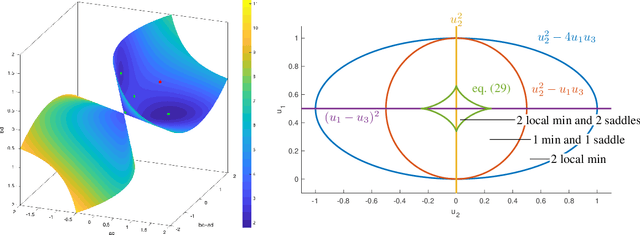
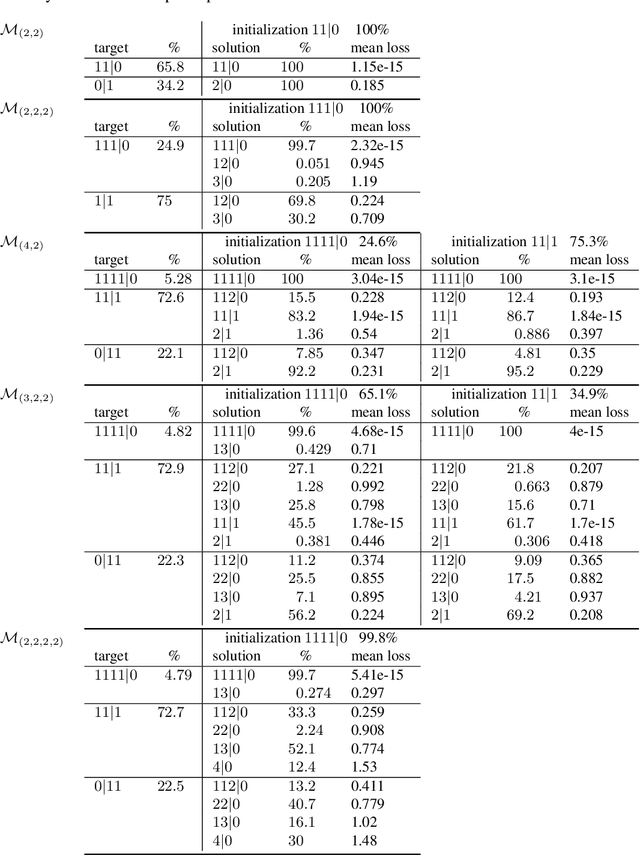
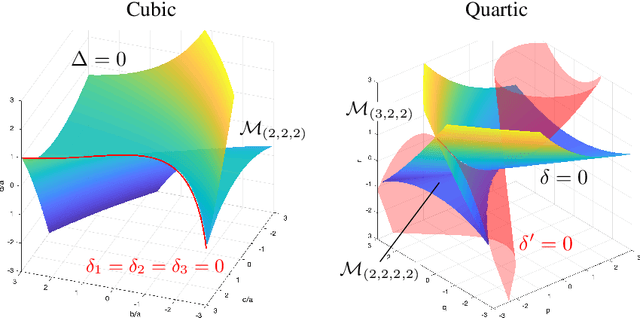
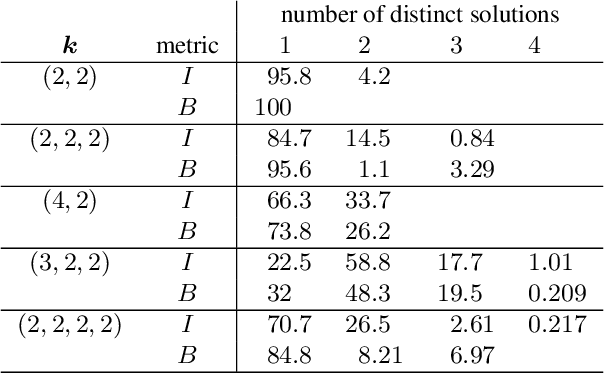
We study the family of functions that are represented by a linear convolutional neural network (LCN). These functions form a semi-algebraic subset of the set of linear maps from input space to output space. In contrast, the families of functions represented by fully-connected linear networks form algebraic sets. We observe that the functions represented by LCNs can be identified with polynomials that admit certain factorizations, and we use this perspective to describe the impact of the network's architecture on the geometry of the resulting function space. We further study the optimization of an objective function over an LCN, analyzing critical points in function space and in parameter space, and describing dynamical invariants for gradient descent. Overall, our theory predicts that the optimized parameters of an LCN will often correspond to repeated filters across layers, or filters that can be decomposed as repeated filters. We also conduct numerical and symbolic experiments that illustrate our results and present an in-depth analysis of the landscape for small architectures.

Semi-supervised NMF Models for Topic Modeling in Learning Tasks

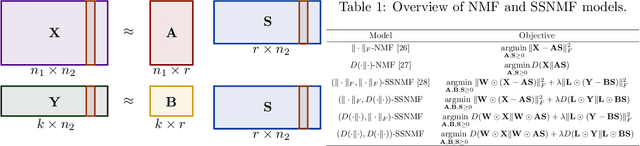
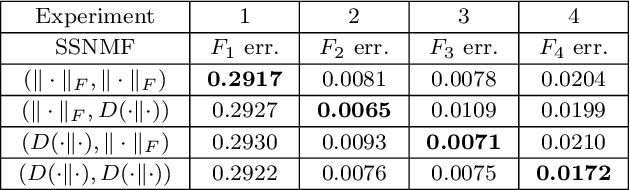
We propose several new models for semi-supervised nonnegative matrix factorization (SSNMF) and provide motivation for SSNMF models as maximum likelihood estimators given specific distributions of uncertainty. We present multiplicative updates training methods for each new model, and demonstrate the application of these models to classification, although they are flexible to other supervised learning tasks. We illustrate the promise of these models and training methods on both synthetic and real data, and achieve high classification accuracy on the 20 Newsgroups dataset.

Stochastic Feedforward Neural Networks: Universal Approximation

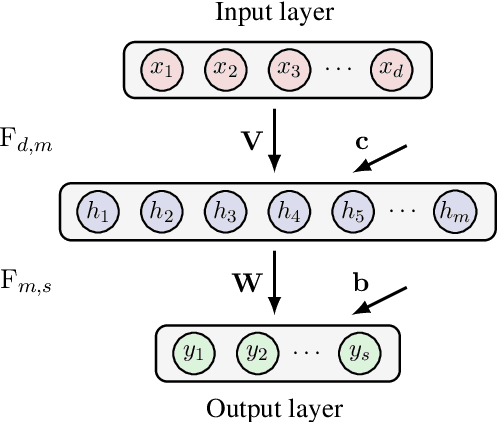
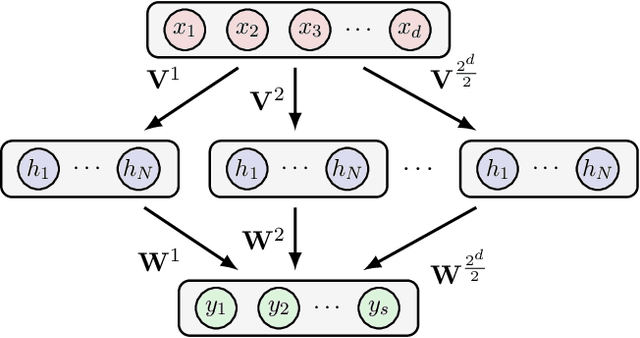
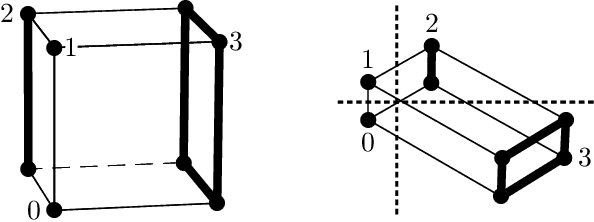
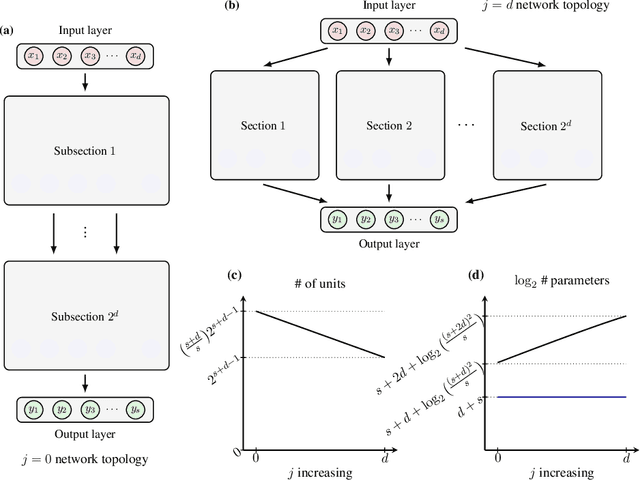
In this chapter we take a look at the universal approximation question for stochastic feedforward neural networks. In contrast to deterministic networks, which represent mappings from a set of inputs to a set of outputs, stochastic networks represent mappings from a set of inputs to a set of probability distributions over the set of outputs. In particular, even if the sets of inputs and outputs are finite, the class of stochastic mappings in question is not finite. Moreover, while for a deterministic function the values of all output variables can be computed independently of each other given the values of the inputs, in the stochastic setting the values of the output variables may need to be correlated, which requires that their values are computed jointly. A prominent class of stochastic feedforward networks which has played a key role in the resurgence of deep learning are deep belief networks. The representational power of these networks has been studied mainly in the generative setting, as models of probability distributions without an input, or in the discriminative setting for the special case of deterministic mappings. We study the representational power of deep sigmoid belief networks in terms of compositions of linear transformations of probability distributions, Markov kernels, that can be expressed by the layers of the network. We investigate different types of shallow and deep architectures, and the minimal number of layers and units per layer that are sufficient and necessary in order for the network to be able to approximate any given stochastic mapping from the set of inputs to the set of outputs arbitrarily well.